 |
|
Числовые характеристики биноминальной случайной величины.
| xi | ||
| pi | q | P |
Пусть x биноминальная случайная величина. Введем вспомогательные случайные величины xi – число появлений события А в отдельном i испытании. Закон распределения каждой случайной величины хi имеет вид:
Тогда M(xi)=0×q+1×p=p
D(xi)=M(xi2) – M2(xi)=02×q+12×p–p2=p-p2=p(1-p)=pq
Для исходной биноминальной случайной величины математическое ожидание и дисперсия имеют следующий вид:
M(x)=M( 
)=n×p (так как слагаемых n штук)
D(X)=D( 
)=npq
Непрерывные случайные величины. Связь плотностью распределения и функцией распределения.
Определение. Случайной величиной называется непрерывной, если она имеет непрерывную функцию распределения, то есть значения непрерывной случайной величины целиком заполняют конечный или бесконечный интервал на числовой оси.
Помимо функции распределения непрерывную случайную величину можно задавать функцией плотности распределения (функция плотности вероятности).
- функция плотности.
- функция распределения (интегральная).
- функция плотности (дифференциальная).
Способы задания для ДСВ.
| Закон распределения | Функция распределения | ||||
| xi | x1 | x2 | … | F(x)=P(X<x) | |
| pi | p1 | p2 | … |
Способы задания для НСВ.
| Функция распредения | Функция плотности |
| F(x)=P(X<x) | f(x)=F(x) |
Свойство функции плотности.
1. Так как F(x) неубывающая Þ f(x)=F’(x)³0
2. 
3. 
Числовые характеристики НСВ.
Математическое ожидание: 
Дисперсия: 
Среднеквадратичное отклонение: s(x)= 
Если все значения НСВ находятся на интервале (a, b), то математическое ожидание:
(a, b) Þ M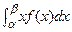(x)= 
D(x)= 
Связь между функцией плотности и функция распределения.
Если известна функция распределения F(x), то можно найти функцию плотности:
F(x) f(x)=F’(x)
Если известна функция плотности f(x), то можно найти функцию распределения следующим образом:
f(x) Þ F(x)= 
Покажем:
F’(x)=( )’=(F(x) 
)’=(F(x)-F(-¥))’=F’(x)=f(x)
F(x)=