 |
|
Умножение на число.
Произведением матрицы 
на число k называется матрица 
такая, что 
).
Пример 2:А= 
, k=2, A 
= 
Матрица –А=(-1) 
А называется противоположной матрице A.
Разность матриц А-В можно определить так: А-В=А+(-В).
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А+В=В+А 5. 1 
А=А
2. А+(В+С)=(А+В)+С 6. 
3. А+О=А 7.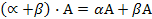 
4. А-А=О 8. 
Где А, В, С – матрицы, 
– числа.
Элементарные преобразования матриц.
Элементарными преобразованиями матриц являются:
· Перестановка местами двух параллельных рядов матрицы;
· Умножение всех элементов ряда матрицы на число, отличное от нуля;
· Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными,если одна из них получается из другой с помощью элементарных преобразований. Записывается А 
.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например.
Произведения матриц.
Операция умножение двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы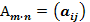 
на матрицу 
называется матрица 
такая, что
…+ 
где 
.
Пример 3: 
Пример 4: А= 
, В= 
. Тогда произведение А 
не определено, так как число столбцов матрицы А (3) не совпадают с числом строк матрицы В (2). При этом определено произведение BхA, которое считается следующим образом:
Матрицы А и В называются перестановочными, если АВ=ВА. Умножение матриц обладает следующими свойствами:
1. 
3. 
2. 
4. 
Если конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспортирования верны свойства:
1. 
2. 
ОПРЕДЕЛИТЕЛИ.
Основные понятия.
Квадратной матрице А порядка n можно сопоставить число det A (или 
, называемое ее определителем, следующим образом:
1. 
Вычисление определителя 2-го порядка иллюстрируется схемой:
Пример 1:
При вычислении определитеся 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:
| (Основания треугольников параллельны побочной диагонали) |
| (Основания равнобедренных треугольников параллельны главной диагонали) |
Пример 2:Вычислить определитель матрицы:
