Здавалка
Главная | Обратная связь

Теорема о ранге матрицы ТЗ.

Ранг матрицы А трансп.задачи на единицу меньше числа уравнений: r(A)=m+n-1.

 

39. Алгоритм построения начального опорного плана ЗЛП.

Для нахождения начального опорного плана можно предложить следующий алгоритм:

1. записать задачу в форме жордановой таблицы так, чтобы все элементы столбца свободных членов были неотрицательными, т.е. выполнялось неравенство аio>=0 (i=1,m). Те уравнения с-мы, в которых свободные члены отрицательны, предварительно умножаются на -1.

2.

  -x1 ….. -xn
0= a1o a11 …. a1n
….. ….. ………………………..
0= amo am1 ….. amn
f= -c1 …. -cn

Таблицу преобразовывать шагами жордановых исключений, замещая нули в левом столбце соответствующими х. При этом на каждом шаге разрешающим может быть выбран любой столбец, содержащий хотя бы один положительный элемент. Разрешающая строка определяется по наименьшему из отношений свободных членов к соответствующем положительным элементам разрешающего столбца. Если в процессе исключений встретится 0-строка, все элементы которой- нули, а свободный член отличен от нуля, то с-ма ограничительных уравнений решений не имеет. Если же встретится 0-строка, в которой, кроме свободного члена, других положительных элементов нет, то с-ма ограничительных уравнений не имеет неотрицательных решений Если с-ма ограничительных уравнений совместна, то через некоторое число шагов все нули в левом столбце будут замещены х и тем самым получен некоторый базис, а следовательно, и отвечающий ему опорный план.

 40. Алгоритм построения оптимального опорного плана ЗЛП. Начальный опорный план Хо исследуется на оптимальность. Если в f-строке нет отрицательных элементов (не считая свободного члена), -план оптимален. Если в f- строке нет также и нулевых элементов, то оптимальный план единственный; если же среди элементов есть хотя бы один нулевой, то оптимальных планов бесконечное множество. Если в f-строке есть хотя бы один отрицательный элемент, а в соответствующем ему столбце нет положительных, то целевая функция не ограничена в допустимой области. Задача не разрешима. Если в f- строке есть хотя бы один отрицательный элемент, а в каждом столбце с таким элементом есть хотя бы один положительный, то можно перейти к новому опорному плану, более близкому к оптимальному. Для этого столбец с отриц-ом элементом в f-строке берут за разрешающий; опред-ют по минимальному симплексному отношению разрешающую строку и делают шаг жорданова исключения. Полученный опорный план вновь исследуется на оптимальность. Это повторяется до тех пор, пока не будет найден оптимальный опорный план либо установлена неразрешимость задачи.   45. Вырожденность и ее устранение при решении задач симплекс-методом. Если среди своб эл-тов есть хотя бы один, равный 0, то план задачи явл вырожденным (опорный или оптим). Геом-ки это означ, что через опорную точку многогранника проходит более n гиперплоскостей вида x1=x2=…=Хn=0. При выборе разреш эл-та наимен симпл отн-ем будет min (Bi/Ais)=0/Ais=0. Вел целевой ф-ции останется прежней, изменится набор баз переменных. В этом случае разреш эл-т выбир-ся по наимен симпл отн-ю своб эл-тов соотв-но к эл-там разреш столбца, исключая нулевое отн-е.   46. Признак бесконечности множества оптимальных планов и геометрическая иллюстрация. Признаком бесконечности множ-ва планов явл-ся наличие в f-строке симплексной т-це, содержащей оптимал.план, хотя бы одного нулевого элем-та не считая свободного члена. Пусть найден оптим.план Х1*, при чем в f-строке один нулевой элемент. Другой оптим.план Х2* можно найти, выбрав в качестве разреш-го столбец с нулевым элементом в f-строке. Остальные оптим. планы можно определить как линейную комбинацию: Х1*= λХ1*+(1-λ)Х2* 0=<λ<=λ  

 

47.Постановка и математич модель ЗЦЛП. В задачах с неделимыми объектами на переменные накладываются условия целочисленности. Иногда эти условия распространяются на все переменные, иногда—на часть переменных. Рассматривают полностью целочисленную задачу f=(n,j=1)∑CjXi max (n,j=1)∑AijXj=bi, i=1,m xj≥0, j=1,n xi-целое,j=1,n Теперь в отличие от общей задачи линейного программирования, оптимальный план не обязательно будет в вершине многогранника планов. Существуют следующие методы решения целочисленных задач: 1.Методы отсечения 2.Комбинаторные 3.Приближенные методы.. Формирование отсекающего неравенства. Идея решения ЗЦЛП методом отсечения и его геометрическая иллюстрация. Идея методов отсечения состоит в следующем: задача решается без учета условия целочисленности. Если полученное решение не является целочисленным, то к условию задачи добавляют новое ограничение, кот называется правильным отсечением. Оно должно удовлетворять 3 условиям: 1.Ограничение должно быть линейным 2.Оно должно отсекать найденное целочисленное решение 3.Оно не должно отсекать не одного целочисленного плана. Расширенная задача подлежит решению, если полученный оптимальный план не целочисленный. Выведем формулу для записи отсекающего неравенства. Допустим, что при решении задачи симпл методом мы получили определенную таблицу. Пусть среди элементов единичного столбца этой матрицы есть дробные-βk.запишем соответствующее ему уравнение Xk=βk-(n-m,s=1)∑αkm+sXm+s Преобразуя это уравнение представим свободные члены и коэфиц как ∑ целой и дробной части. Xk=([βk]-(n-m,s=1)∑[αkm+s]Xm+s)+({βk}-(n-m,s=1)∑ {αkm+s}Xm+s) Сумма в первых скобках-целое число, во вторых-дробное. Для того, чтобы Хк было целым, надо, чтобы и сумма во вторых скобках была целой. Обозначим ее Sk={βk}-(n-m,s=1)∑ {αkm+s}Xm+s Чтобы s было целым оно должно быть не положительным (n-m,s=1)∑ {αkm+1}Xm+1≥{βk} (1)   48.Алгоритм метода Гомори. 1.Симплекс-методом находят оптимальный план задачи. Если все компоненты оптимального плана целые, то он –оптимальный. В противном случае переходят к пункту 2 2.Среди нецелых компонент следует выбрать ту, у которой дробная часть является наибольшей и по соответствующей этой строке симплексной таблицы сформулировать правильное отсечение по формуле (n-m,s=1)∑ {αkm+1}Xm+1≥{βk} 3.Сформулированное неравенство преобразовать в эквивалентное нулевое равенство и включить в симплексную таблицу с нецелочисленным оптимальным планом 4.Полученную расширенную задачу решают симплекс-методом. Если полученный план не является целочисленным нова переходят к пункту 2. Если в процессе решения появится строка с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В таком случае и исходная задача неразрешима в целых числах.Метод Гомори имеет ограниченое применение. С его помощью целесообразно решать небольшие задачи, т.к. число интераций может быть очень большим.   49.Метод ветвей и границ решения целочисленных задач. Этот метод относится к группе комбинаторных. Применение этих методов заменяет полный перебор планов их частным перебором. Идея метода: пусть дана ЗЦЛП f=(n,j=1)∑CjXi max (n,j=1)∑AijXj=bi, i=1,m xj≥0, j=1,n xi-целое,j=1,n Сначала в ОДЗ этой задачи определяется оптимальный план без учета условия целочисленности. Если в полученном решении некоторые переменные имеют дробное значение, то выбирают любую из дробных переменных и разветвляют исходную задачу на 2 подзадачи f =∑CjXj max f =∑CjXj max (n,j=1)∑AijXj≤bi, i=1,m (n,j=1)∑AijXj≤bi, i=1,m Xk≤[Xk˚] Xk≥[Xk˚]+1 Xj≥0 Xj≥0 Xj-целое,j=1,n Xj-целое,j=1,n Если после решения этих подзадач неизвестные не будут целочисленные, то выбирается задача с большим значением целевой функции и по неизвестной Задача разбивается на 2 новые подзадачи. На каждом последующем шаге сравниваются целевые функции неразветвленных задач и ветвиться задача с большим значением целевой функции.  

 

50.Понятие о динамич прог. Особ-ти реш-я задач. Динамич программирование—математический метод для нахождения оптим решений многошаговых задач. Многошаговымявл процесс, развивающийся во врем и распадающийся на ряд шагов, или этапов. Одна из особ-тей метода динамич прог сост в том, что принятые решя по отн-ю к многошаг процессам рассм-ся не как единичный акт, а как целый комплекс взаимосвяз решений. Эту послед-ть взаимосвяз решений наз стратегией.Цель оптим план-я—выбрать стратегию, обеспеч получ-е наилучшего рез-та с т. зр. заранее выбранного критерия. Такую стратегию наз оптим. Др важной особ-тью метода явл незав-ть оптим реш-я, принимаемого на очередном шаге, от предыстории, т.е. от того, каким обр оптимизируемый процесс достиг теперешнего сост-я. Оптим реш-е выбир-ся лишь с учетом факторов, характе-ющих процесс в данный момент. Метод динам программ характеризуется также тем, что выбор оптим реш-я на каждом шаге должен произв-ся с учетом его последствий в будущем. Это означает, что, оптимизируя процесс на каждом отдел шаге, ни в коем случае нельзя забыть обо всех последующих шагах. Принцип оптимальности Беллмана. Рекуррентное соотношение Беллмана. Метод динам прогр позволяет одну задачу со многими переменными заменить рядом последовательно решаемых задач с меньшим числом переменных. Решение осуществляется по шагам. Осн принцип, на котором баз-ся оптим-ция многошаг процесса, а также особ-ти вычислит метода—принцип оптим-ти Беллмана. Оптим повед-е обладает тем св-вом, что каковы бы ни были начальное сост-е и нач реш-е, последующие реш-я должны быть оптим относит-но сост-я, получ в рез первонач решя. Математически он записывается вырем вида: fn-1(Sl)=optimum(Rl+1(Sl,Ul+1)+fn-(l+1)(Sl+1)) (1) ul+1 (l=0,n-1) Optimum в выражении означ max или min в завис от усл-я задачи. Все вычисл-я, дающие возм-ть найти оптим знач-е эф-та, достигаемого за n шагов, fn(S0), проводятся по формуле (1), кот носит назв-е осн функционального ур-ия Беллмана или рекуррентное соотн-е.При вычислении очередного знач-я ф-ции fn-1 исп-ся знач-е ф-ции fn-(l+1), получ на предыдущем шаге, и непосредственное знач-е эф-та Rl+1(Sl,Ul+1), достигаемого в рез выбора решения Ul+1 при заданном сост-ии с-мы Sl. Процесс вычисл-я знач-я ф-ции fn-1(l=0,n-1) Осущ-ся при естеств нач условии f0(Sn)=0, кот означ-, что за пределами конечного сост-я с-мы эф-т равен 0.   Вычислительная схема метода динамического программирования. Оптим реш-е задачи методом динамич прог нах-ся на осн функционального уря fn-1(Sl)=optimum(Rl+1(Sl,Ul+1)+fn-(l+1)(Sl+1)) (1) ul+1 (l=0,n-1) Чтобы определить его, необх-мо: 1.записать функц ур-е для последнего сост-я процесса (ему соответствует l=n-1) fn-1(Sl-1)=optimum(Rn(Sn-1,Un)+f0(Sn)) ul+1 2. найти Rn(Sn-1,Un) из дискретного набора его значений при некот фиксир Sn-1 и Un из соотв допустимых обл (так как f0(Sn)=0, то f1(Sn-1)= optimum(Rn(Sn-1,Un) Un В рез после 1ого шага известно реш-е Un и соотв знач-е ф-ции f1(Sn-1) 3.Уменьшить знач-е l на единицу и записать соотв функц ур-е. При l=n-k (k= 2,n) оно имеет вид fk(Sn-k)=optimum(Rn-k+1(Sn-k,Un-k+1)+fk-1(Sn-k+1)) (2) Un-k+1 4.найти условно-оптим реш-е на основе выр-я (2) 5.проверить, чему равно знач-е l.Если l=0, расчет условно-оптим реш-ий закончен, при этом найдено оптим реш-е задачи для 1ого сост-я процесса. Если l не равно 0, перейти к выполнению п.3. 6.Вычислить оптим реш-е задачи для каждого послед шага процесса, двигаясь от конца расчетов к началу.   51. Задача о выборе кратчайшего пути по сети дорог и реш-е ее методом динамич прог. Надо перевезти груз из А в Б, известна сеть дорог, их соединяющих. Каждой дуге приписана стоимость перевозки груза. Надо определить наиболее экономичный маршрут. Рассматривается некоторый управляемый процесс. В результате управления система переводится из состояния S0 в состояние S. Предположим, что управление может разбиться на n шагов, на кождом из которых выбирается одно из множества допустимых управлений Un (n=1,N). Элементы множества Un и Sn определяются из условия задачи.   На каждом шаге достигается эффект Zn. Общий эффект это сумма эффектом, достигнутых на каждом шаге. Тогда задача динам программир будет формулироваться: Определит такое допустимое управление U*=(U1, U2, .. ,UN), переводящее систему из состояния S0 в состояние SN, при котором общий эффект Решение задач методом динамического программирования осуществляется на основе принципа оптимальности.   S4=10, S5=11 S3=min(12+S4, 9+S5)=min(12+10? 9+11)=20 S2=min(8+S4, 15+S5)=min(8+10, 15+11)=18 S1=min(4+S2, 7+S3)=min(4+18, 7+20)=22
2
1
3
4
5
6

 

 


52. Задача об оптим распред-ии ср-в м/у предпр-ями на расшир-е пр-ва и реш-е ее методом динамич прог. В 1 из праздничных дней в 3 пункта города необх-мо отправить 5 автолавок с прод пит-я. За прошедшие годы изучен спрос насел-я, что задается табл. Необх-ио опред-ть max товарооб-т от 3 пунктов города, в кот посылается 5 автолавок.
Кол-во автолавок Товарооб-т G (Xi)
№1 №2 №3

Функц ур-е:

F#(5)=max0<=x<=5(g3(x)+f2(5-x))

F2(5)=max0<=x<=5(g2(x)+f1(5-x))

F1(x)=g1(x)

 

F2(5)=max0<=x<=5=(14+0, 10+4, 8+6, 4+5, 3+12, 15+0)=15

Вспом табл:

Xi G1 F1 G2 F2 G3 F3

F3(5)max=18 млн ден ед

 

Х3*=1 Х2*=4 Х1*=0

Или

Х3*=1 Х2*=1 Х1*=3

 54.Постановка задачи НЛП. Трудности, возник при реш-ии задач НЛП. Понятие выпуклой и вогнутой функции. Общая задача нелин прог ставится след обр: треб-ся найти знач-е n переменных x1,x2,…,xn, кот удовл-ют m ур-ям и нерав-вам φi=(x1,x2,…,xn){≥,=.≤}bi (i=1,m) и максим-ют ф-цию z=f(x1,x2,…,xn) Трудности реш-ия задач связ с тем, что в нелинх задачах допустимая обл м. б. невыпуклой, может иметь бесконечное число крайних точек, целевая ф-я может достигать экстремума не только на границе, но и внутри обл и иметь неск лок экстремумов. С геом т. зр. задача нелин прог сводится к нах-ю выпуклой обл-, определяемой с-мой ограничений и точкой, через кот проходит линия ур-я поверх-ти, задаваемая целевой ф-цией, соотв-ющая наибол (наимен) знач-ю ф-ции. Функция f(x), определенная на выпуклом множестве Х называется выпуклой, если для любых точек х1,х2 из этого множества и любого 0≤λ≤1 справедливо неравенство f(λx1+(1-λx2)≤λf(x1)+(1-λ)f(x2) (1) Если в соотношении 0<λ<1 и любых х1 и х2 принадлежит Х (х1≠х2) имеет место строгое неравенство, то f(x)—строго выпуклая. Примерами выпуклых множеств является квадрат, круг, пирамида. Функция f(x), определенная на выпуклом множестве Х называется вогнутой, если для любых точек х1,х2 из этого множества и любого 0≤λ≤1 справедливо неравенство f(λx1+(1-λx2)≥λf(x1)+(1-λ)f(x2) (2) Если в соотношении 0<λ<1 и любых х1 и х2 принадлежит Х (х1≠х2) имеет место строгое неравенство, то f(x)—строго вогнута. f(x)=f(x1,x2,..xn)—дифференцирована в точке Х0, то градиентом функции f(x) называется n мерный вектор, координаты которого равна частным производным. Grad f(X0)= f(X0).   55. Графич метод реш-я задач НЛП. Реш-ся как и в ЛП. Строится ОДР. Придается целевой ф-ции пост знач-е const. Опред-ся линия уровня. 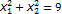x1>=0, x2>=0 f=2x1+x2(max)
X1
X2
С опт
Линия ур 1)
Касательная 3)
Перпендикуляр 2)
r=3 f=0 x2=-2x1 k1=-2

 

 

Находим ур-е ОС:

X2=k2*x1

K1*k2=-1 усл-е перпендик-ти

-2k2=-1 K2=1/2 X2=1/2x1

 

x2=1/2x1

 

x1*=1,2 x2*=0,6

f max=2*1/2 +0,6 =3

 

Граф метод ограничен тем, что применим для случая 2 переменных, простейших случ 3 переменных.

 

56.Метод Лагранжа решения задач НЛП. Точка усл экстремума х2=х12 Х2’=2х1=0, х1=0, х2=0, х*=(0,0) Доп огранич-е: х1=1 Х2max=12=1 Чтобы найти точку усл экстр ф-ции, строится ф-ция Лагранжа, учит-ющая доп огранич-я. Метод применим, когда с-ма огр-ий предст собой рав-во. Целевая ф-ция непрер, диффер-ма, им производную по крайней мере 2 порядка. На переменные не наклад-ся усл неотрицат-ти, целочисл-ти. Ф-ция Лагранжа строится, чтобы усл экстр заменить на безусл. В с-му орг-ий вводим столько множ-лей λi, сколько равенств. Если i=1,…,m, то λ1, λ2, …, λm. Ф-ция Лагранжа запис-ся след обр: L(X1,X2,X3,..Xn,λ1,λ2,…,λm)=f(x1,x2,..,xn)+(m,i=1)∑λi(bi-φi(x1,x2,…,xn)) Найти частные производные ф-ции Лагранжа по всем переменным, приравнять к 0. Решить с-му ур-ий, опуская множ-ли λi. В рез получим стационарную точку усо экстр. Чтобы опред-ть в ней max/min, надо найти 2ой диффер-л ф-ции Лагранжа по ф-ле: 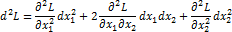Если >0, то им min Если <0, то им max Если , то надо провести доп расчеты, кот в итоге приведут к отсутствию реш-я   57. Градиентный метод реш-я задач НЛП. В ОДР выбир-ся произвол точка х0. Если их нее переместить по разным направл-ям на одинак расстояние, то приращ-е цел ф-ции будет неодинак. Вектор с координатами частных производных цел ф-ции наз градиентом. В каждой точке свой градиент. grad f=(0,0,…,0)X0 Им помлед-ть точек x0<x1<x2<x3<…<Cопт Точка опт достигается за бесконечное число шагов, иногда за конечное.   Пример. Определить параметр λ из усл перпендик-ти линии ур. (grad f)X0+(grad f)X1=0 F=x12+x22-2x1-2x2(min) X0=(1,3) Grad f=(2x1-2, 2x2-2)(1,3)=(0,4) 58. Метод искусств базиса реш-я задач ЛП симплекс методом. Если с-ма огр-ий предст-ся в виде равенств, то с пом балансовых переменных, кот практически равны 0, задача предст-ся в канонич форме, и балансовые искусств переменные приним-ся за базисные. Х1+2х2=8 4х1+3х2=17 Х1>=0 x2>=0 F(x)=2x1+3x2(max)   С искусств переменными: X1+2x2+x3=8 4x1+3x2+x4=17 Xj>=0, j=1,2,3,4 F(x)=2x1+3x2-m(x3+x4)(max) m-достаточно большое число   Баланс переменные: Х3=8-х1-2х2 х4=17-4х1-3х2 Строит исх табл преобразований, где одной индексной строкой опред-ем эл-ты, не связ с m, а 2ой – эл-ты, связ с искусств перем. При переходе искусств баз переем в своб столбей, соотв своб переем, опускаются.
БП СП
-х1
Х2 ½
Х4 5/2
f -1/2

 

БП
Х2
Х1
f

Х*=(х1*, х2*)=(2,3)

F(x*)=2x1+3x2-m(8-x1-2x2+17-4x1-3x2)=2x1+3x2-25M+5Mx1+5Mx2(max)=13

    

 

1. Предмет и задачи МП. Экон примеры. Постановка общей задачи МП. 2. Задача ЛП и разл формы ее мат. записи (общая, каноническая, симметричная). Преобр-е одной формы записи ЗЛП в др. 3. Целевая ф-ция и ее св-ва, интерпр-ция. Осн понятия планов: допуст, баз, оптим. ОДР ЗЛП. 4. Граф метод реш-я ЗЛП. 5. Опорные планы ЗЛП. Соотв-е м/у опорными планами и вершинами многогранника планов. 6. Осн теорема ЛП. Принцип схема реш-я ЗЛП, вытек из этой теор. 7. Симпл метод реш-я ЗЛП. Общая идея. Геом ил-ция. 8. Признак оптим-ти опорного плана ЗЛП 9. Нах-е нач опорного плана ЗЛП. 10. Нах-е оптим- опорного плана ЗЛП 11. Признак неогр-ти цел ф-ции на мн-ве планов и геом ил-ция. 12. Признак бескон-ти мн-ва оптим планов (альтерн оптимум) и геом ил-ция. 13. Признак неразреш-ти ЗЛП и геом ил-ция 14. Алгоритм симплекс-метода. 15. Понятие двойств-ти в ЛП. Симметр двойств задачи и их экон интерп-ция. Двойств оценки. 16. Несим двойств задачи. Связи м/у эл-тами моделей задач двойств пары. Соотве м/у переменными двойств задач (двойств переменные). 17. Теорема двойств-ти (осн теорема двойств-ти) и ее – экон интерп-ция. Нах-е оптим плана двойств задачи по реш-ю прямой. 18. Теорема об оценках и ее экон интерп-ция 19. Св-ва двойств оценок и их прим-е при анализе решений ЗЛП. 20. Форм-ка и матем модель трансп задачи по критерию ст-ти. Особ-ти модели как ЗЛП. 21. Трансп задача с откр и закр моделью. Преобр-е откр модели в закр. 22. Усл разреш-ти транспй задачи. Усл-я целочисл-ти оптим плана. 23. Теор о ранге матрицы с-мы ограничит урий трансп задачи и ее прикладное знач-е. 24. Циклы в трансп табл. Св-ва циклов. 25. Способы построения нач опорного плана трансп задачи (северо-зап угла, наимен эл-та, Фогеля). 26. Проц-ра преобр-я опор плана трансп задачи в новый опор план. 27. Оценка (хар-ка) свобй клетки трансп табл, ее вычисл-е и экон смысл. 28. Признак оптим-ти опор плана трансп задачи. Неединств-ть оптим плана. 29. Потенциалы поставщиков и потр-лей и их вычисл-е. 30. Связь м/у оценками своб клеток, и потенц-ами. 31. Алгоритм метода потенциалов.   32. Осн нерав-во теории двойств-ти. 33. Теорема сущ-я оптим планов пары двойств задач. 34. 1ая теорема теории двойств-ти. 35. 2ая теорема теории двойств-ти. 36. Эконометрич смысл двойств оценки. Интервал устойч-ти двойств оценок. 37. Теорема о сущ-ии плана трансп задачи. 38. Теорема о ранге матрицы трансп задачи. 39. Постановка и реш-е задачи об оптим назн-ях. 40. Ассортиментно-распределит задачи, постановка и реш-е. 41. Алгоритм построения опорного плана симплекс-методом. 42. Алгоритм построения оптим плана симплекс-методом. 43. Теорема о выборе разреш эл-та задачи, решаемой симплекс-методом. 44. Теорема об оптим плане задаче, решаемой симплекс-методом. 45. Вырожд-ть и ее устранение при реш-ии задач симпл методом. 46. Случай бесчисл мн-ва оптим планов. Геом ил-ция. 47. Постановка и матем модель задачи ЦЛП. Идея реш-я задачи методом отсечений и его геом ил-ция. 48. Метод Гомори реш-я полностью целочисл задачи ЛП. 49. Метод ветвей и границ реш-я целочислзадач. 50. Понятие о динамич прогр-ии. Особ-ти реш-ия задач. Принцип оптим-ти Беллмана. Вычислит схема метода динамич прогр-я 51. Задача о выборе кратчайшего пути на сети дорог и реш-е ее методом динамич прогр-я. 52. Задача об оптим распред-ии срв м/у предпр-ями на расширение пр-ва и реш-е ее методом динамич прогря. 53. Графич метод реш-я задач дробно-линейного прогр-я. 54. Постановка задачи НЛП. Понятие выпуклой и вогнутой функции 55. Графич метод реш-я задач НЛП. 56. Метод Лагранжа реш-я задач НЛП. 57. Градиентный метод реш-я задач НЛП. 58. Метод искусств базиса реш-я задач ЛП симпл методом. 59. Симпл метод реш-я задач дробно-линейного прогр-я. 60. Постановка задачи параметричо ЛП. Симпл метод реш-я параметрич задач.    

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

     

 

 





©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.