 |
|
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Степенные ряды.
Обобщим понятие числового ряда следующим образом: рассмотрим ряд, в котором элементами являются не числа, а функции. Такой ряд называется функциональным.
Определение. Выражение вида
называется функциональным рядом.
Дадим определение степенного ряда, который является важным частным случаем функционального.
Определение. Функциональный ряд вида
,
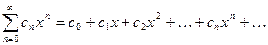где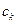 
-- числа, не зависящие от 
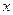, называется степенным рядом.
Ряд вида
также является степенным и называется рядом по степеням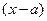 
, здесь 
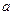-- число.
При любом фиксированном значении 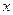степенной ряд превращается в числовой, который либо сходится, либо расходится.
Определение. Множество всех значений переменной 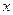, при которых степенной ряд сходится, называется его областью сходимости.
Всякий степенной ряд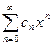 
сходится при 
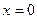, соответственно ряд 
сходится при 
.
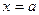Имеет место терема:
Область сходимости степенного ряда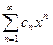 
– это
либо интервал 
,
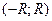либо полуинтервал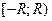 
,
либо полуинтервал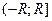 
,
либо отрезок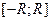 
,
либо вся числовая прямая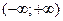 
,
либо одна точка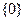 
.
Число 
называют радиусом сходимости степенного ряда
Для ряда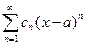 
вид области сходимости аналогичен, только все сдвигается на величину .
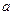Число 
может принимать любые неотрицательные значения. В частности, если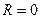 
, то ряд сходится в одной точке 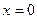, если 
степенной ряд сходится на всей числовой прямой.
Для нахождения области сходимости степенного ряда обычно используют признак Даламбера. Кроме того, существует формула (Коши-Адамара) для нахождения радиуса сходимости степенного ряда:
.
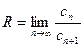При 
и при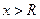 
ряд расходится, а поведение ряда при 
подлежит отдельному исследованию.
Задача №1.Найти область сходимости степенного ряда 
.
Решение. Применим признак Даламбера:
, 
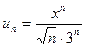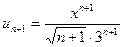, тогда
.
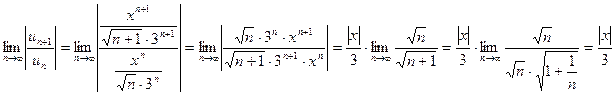Ряд сходится, если
, т.е.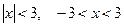 
.
Таким образом,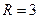 
.
Исследуем поведение ряда на концах интервала сходимости.
Пусть 
. Подставим это значение в формулу для исходного ряда. Получим положительный ряд
.
Он расходится как обобщенный гармонический, 
.
Следовательно, значение не принадлежит области сходимости.
Пусть 
. Тогда получаем числовой ряд
,
который является знакопеременным. Исследуем его на абсолютную сходимость. Для этого рассмотрим ряд, составленный из абсолютных величин членов этого ряда:
.
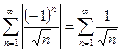Получили положительный обобщенный гармонический ряд, который расходится, поскольку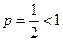 
. Следовательно, исследуемый знакопеременный ряд 
не сходится абсолютно.
Дальнейшее исследование на сходимость проведем, используя признак Лейбница.
Ряд является знакочередующимся.
1) Модули членов ряда монотонно убывают: 
.
2) Модуль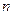 
-го члена ряда стремится к нулю: 
.
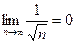Поскольку все условия признака Лейбница выполняются и ряд не сходится абсолютно, то ряд сходится условно. Таким образом, при степенной ряд сходится.
Теперь можно записать ответ.
Ответ: Область сходимости: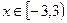 
.
Степенной ряд вида
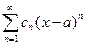
имеет интервал сходимости, симметричный относительно точки 
,
интервал сходимости имеет вид
,
поведение ряда при 
и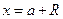 
подлежит, как и в предыдущем случае, дополнительному исследованию.
Задача №2.Найти область сходимости степенного ряда 
.
Решение. Для нахождения интервала сходимости используем, как и прежде, признак Даламбера:
, 
,
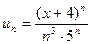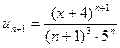Степенной ряд сходится, если
,
отсюда имеем:
,
следовательно, радиус сходимости степенного ряда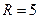 
.
,
интервал сходимости симметричен относительно точки 
.
Теперь необходимо выяснить, как ведет себя степенной ряд на концах интервала сходимости.
Пусть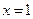 
. После подстановки этого значения в степенной ряд получим:
.
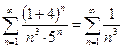Это сходящийся обобщенный гармонический ряд и значит число 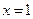принадлежит интервалу сходимости.
Пусть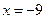 
. Подставим это значение в исходный ряд вместо :
.
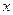Получили знакочередующийся числовой ряд, который будем исследовать на абсолютную сходимость, т.е. будем исследовать ряд
.
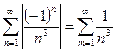Этот положительный ряд сходится как обобщенный гармонический при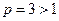 
.
Отсюда следует, что знакопеременный ряд
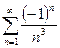
сходится абсолютно и значение 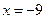принадлежит интервалу сходимости.
Ответ: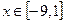 
.
Задача №3.Найти область сходимости ряда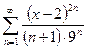 
.
Решение. 
, 
.
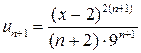Вычислим предел:
Интервал сходимости находим из неравенства
:
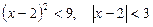, т.е.
радиус сходимости ,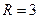 
.
Интервал сходимости имеет вид: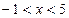 
.
Исследуем поведение ряда на границах интервала сходимости.
Подставим значение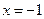 
в исходный ряд:
.
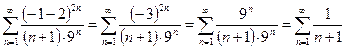Ряд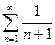 
расходится. Таким образом, при 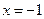степенной ряд расходится.
При 
получим:
,
Следовательно, при степенной ряд расходится.
Ответ. Область сходимости: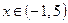 
.
Задача №4.Найти область сходимости ряда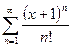 
.
Решение.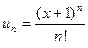 
, 
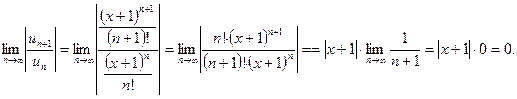
Мы получили, что 
независимо от значения 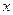, следовательно,
при любом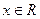 
степенной ряд сходится, поэтому область сходимости ряда – вся числовая прямая.
Ответ: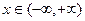 
.
Задача №5.Найти область сходимости ряда 
.
Решение.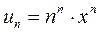 
, 
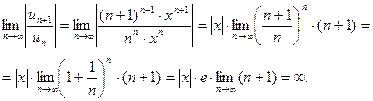
Степенной ряд расходится при любом значении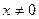 
.
Ответ: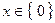 
.