 |
|
Функциональные свойства суммы ряда
10. Непрерывность.
Теорема 1.
Если члены функционального ряда 
определены на отрезке 
и ряд равномерно сходится на этом отрезке, то в точках непрерывности функций сумма ряда 
непрерывна.
Доказательство.
Пусть непрерывны в точке 
.
Так как 
, 
, то для 
верно неравенство
Возьмем 
и разделим его на 3. По определению равномерной сходимости найдется такой номер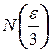 
, что при всех 
и всех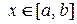 
выполняется неравенство 
. Значит, и 
. Далее фиксируем некоторое . Функция 
как сумма непрерывных функций непрерывна в точке 
. Поэтому для 
найдется 
такое, что как только 
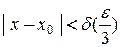, то выполняется неравенство 
.
Окончательно имеем 
. ■
20. Почленное интегрирование функционального ряда.
Теорема 2.
Если члены функционального ряда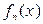 
непрерывны 
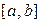и ряд равномерно сходится на этом отрезке, то его можно почленно интегрировать, т.е.
.
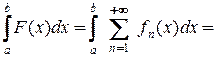
Доказательство.
Существование всех интегралов, указанных в теореме, очевидно. Докажем, что сходится ряд
. (**)
Проинтегрируем равенство , получим
или
.
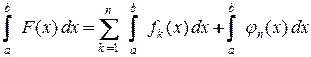Далее установим, что 
. Для этого возьмем сколь угодно малое и для числа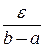 
, используя равномерную сходимость, найдем номер 
, такой, что при всех 
и всех 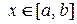выполняется неравенство 
. Проведем оценку
, что и означает
.
Для частичных сумм ряда (**) верно
.
При 
правая часть имеет предел, следовательно, частичные суммы ряда (**) имеют предел, а именно предел, равный 
. ■
30. Почленное дифференцирование функционального ряда.
Теорема 3.
Если члены функционального ряда непрерывно дифференцируемы на , ряд 
сходится на этом отрезке, а ряд 
сходится равномерно, то сумма ряда 
является непрерывно дифференцируемой функцией и 
.
Доказательство.
Обозначим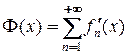 
, по условию, этот ряд составлен из непрерывных функций и равномерно сходится, поэтому проинтегрируем его по отрезку 
.
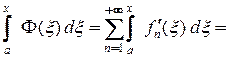
Итак, 
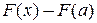, слева в этом равенстве стоит интеграл с переменным верхним пределом, он имеет производную по этому пределу, равную подынтегральной функции 
. Следовательно, существует и производная правой части, т.е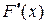 
. Окончательно получаем 
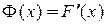или .
Замечание. В теоремах 1-3 нельзя убрать требование равномерной сходимости (т.е. ряд может сходиться неравномерно к разрывной функции), с другой стороны, это требование не является необходимым (например, ряд может сходиться к непрерывной функции, но неравномерно).