Главная | Обратная связь

Теоретическое введение

Ряды и их приложения

1.1.1 Числовые ряды
Пусть дана последовательность чисел a₁, a₂, a₃, ..., a_n, a_n+1, ... . Выражение вида

a1 + a2 + a3 + ... + an + an+1 + ... = an

(1.1)

называется числовым рядом. Числа a₁, a₂, a₃, ... , a_n, ... называются членами (элементами) ряда; a₁ – первый член, a₂ – второй член, ... , a_n – ­ n-ый или общий член ряда.
Сумма S_n первых n членов числового ряда:
S_n = a₁ + a₂ + a₃ + ... + a_n
называется его частичной суммой. Так как число членов ряда бесконечно, то частичные суммы ряда образуют последовательность частичных сумм: ­ ­ S₁, S₂, S₃, ... , S_n.
Числовой ряд, получающийся из ряда (1.1) отбрасыванием его первых n членов, называется остатком числового ряда (1.1) и обозначается r_n : ­ ­
r_n = a_n+1 + a_n+2 + ... .
Определение. Числовой ряд (1.1) называемся сходящимся, если существует конечный предел последовательности его частичных сумм:
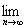S_n = S.
Число S в этом случае называется суммой ряда (1.1).
Если же предел последовательности частичных сумм S_n равен бесконечности или не существует, то ряд называется расходящимся. Расходящийся ряд суммы не имеет.
Для исследования числовых рядов используются признаки сходимости, по которым можно установить сходится ряд или расходится. Приведем здесь те признаки, которые используются для выполнения типового расчета.

Для знакоположительных рядов (рядов с положительными членами) справедлив:
Признак сравнения, связанный с пределом. Пусть даны два знакоположительных ряда a_n (ряд А) и b_n (ряд В) и существует предел = C, где С – положительное число, т.е. С > 0. Тогда, если сходится ряд (В), то сходится и ряд (А). Если расходится ряд (В), то расходится и ряд (А). Т.е. ряды (А) и (В) ведут себя одинаково.
Признак сравнения, связанный с пределом, справедлив, в частности, в том случае, когда a_n и b_n эквивалентные последовательности, т.е. = 1. Эквивалентность последовательностей обозначается a_n ~ b_n.
В качестве ряда, с которым удобно производить сравнение рядов, часто используется ряд , который называется обобщенным гармоническим рядом или рядом Дирихле. Этот ряд сходится при p > 1 и расходится при p ≤ 1.
При этом удобно использовать следующее свойство многочленов: ­ многочлен P_m(x) = a₀x^m + a₁x^m-1 + ... + a_m-1x + a_m при x → + ∞ эквивалентен своему слагаемому a₀x^m , т.е. P_m(x) ~ a₀x^m. Справедливо и более общее утверждение: алгебраическая сумма степенных функций с различными положительными степенями эквивалентна при x → + ∞ своему слагаемому, в котором степень наибольшая. Например, при x → + ∞

Пример. Исследовать на сходимость ряд .
Решение. В нашем случае a_n = . Воспользуемся признаком сравнения, связанным с пределом. Согласно приведенному выше свойству многочленов, числитель рассматриваемой дроби 3n² + 5n – 1 при n → ∞ эквивалентен слагаемому 3n², знаменатель дроби 6n⁴ + 3n² + 7 при этом эквивалентен слагаемому 6n⁴, тогда
.
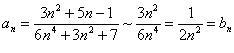Ряд из b_n отличается от обобщенного гармонического при p = 2 > 1 только множителем и поэтому сходится. Следовательно, ряд из a_n сходится по признаку сравнения, связанному с пределом.

Для знакоположительных рядов также часто используется
Признак Даламбера. Пусть дан знакоположительный ряд aⁿ и существует предел . Тогда при ρ < 1 ряд сходится, при ρ > 1 ряд расходится.
Пример. Исследовать на сходимость ряд .
Решение. Находим
.
Так как ρ = < 1, то данный ряд сходится по признаку Даламбера.
Для знакопеременных рядов, в которых встречаются как положительные так и отрицательные слагаемые, справедлив признак абсолютной сходимости.
Признак абсолютной сходимости. Если для знакопеременного ряда

a1 + a2 + a3 + ... + an + ... = an

(1.2)

сходится ряд, составленный из абсолютных величин его членов:
|a₁| + |a₂| + |a₃| + ... + |a_n| + ... = |a_n|,
то заданный ряд (1.2) также сходится.
Признак абсолютной сходимости является достаточным, но не необходимым. Это означает, что существуют знакопеременные ряды, которые сходятся, в то время как ряды, составленные из абсолютных величин их слагаемых, расходятся. В связи с этим вводятся следующие определения.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
В практических задачах часто встречаются знакочередующиеся ряды, в которых за каждым положительным членом следует отрицательный, а за каждым отрицательным – положительный. Такой ряд можно записать в виде

a1 – a2 + a3 – a4 + ... + (–1)n+1an + ... = (–1)n+1an,

(1.3)

где a₁, a₂, a₃, ... , a_n, ... – положительные числа. (Мы записали, что первый член знакочередующегося ряда положителен. Исследование знакочередующегося ряда с отрицательным первым членом сводится к исследованию ряда (1.3) умножением всех его членов на –1).

Знакочередующиеся ряды исследуют с помощью достаточного признака сходимости Лейбница.
Признак Лейбница. Если в знакочередующемся ряде (1.3) абсолютные величины членов не возрастают: a₁ ≥ a₂ ≥ a₃ ≥ a₄ ≥ ... ≥ a_n ≥ ... и общий член ряда стремится к нулю: 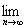a_n = 0, то ряд сходится.
Важной практической задачей является вычисление суммы ряда. Будем искать сумму ряда с заданной точностью ε > 0, т.е. найдем такое n, чтобы выполнялось неравенство |S – S_n| < ε, где S – сумма ряда, S_n - его частичная сумма. Тогда S_n будет суммой нашего ряда с точностью ε. Но S – S_n = r_n – остаток ряда. Таким образом, задача сводится к нахождению такого n, чтобы выполнялось условие |r_n| < ε, а затем вычислению частичной суммы S_n.
Если знакочередующийся ряд сходится по признаку Лейбница, для остатка ряда справедлива оценка:
|r_n| ≤ |a_n+1|.
Т.е. остаток ряда по абсолютной величине не превосходит абсолютной величины первого слагаемого этого остатка.

1.1.2 Функциональные ряды
Пусть дана последовательность функций u_n(x), n = 1, 2, 3, ... , определённых на множестве D.
Определение. Выражение вида
u₁(x) + u₂(x) + ... + u_n(x) + u_n+1(x) + ... = u_n(x)
называется функциональным рядом. Множество всех точек, для которых функциональный ряд сходится, называются областью его сходимости. Соответственно, множество всех точек, для которых ряд сходится абсолютно, называется областью абсолютной сходимости.
Важным частным случаем функциональных рядов являются степенные ряды. Степенным рядом называется ряд, члены которого – степенные функции:
a₀ + a₁(x – a) + a₂(x – a)² + ... + a₂(x – a)ⁿ + ... = a_n(x – a)ⁿ,
где a и коэффициенты ряда a₀, a₁, a₂, ... , a_n, ... – постоянные числа. При a = 0 степенной ряд имеет вид:

a0 + a1x + a2x2 + ... + anxn + ... = anxn.

(1.4)

Важный вопрос – область сходимости такого ряда. Ответ даёт теорема Абеля.
Теорема Абеля. Если ряд (1.4) сходится не при всех значениях х, но сходится в некоторой точке x₀ ≠ 0, то существует число R > 0, называемое радиусом сходимости, такое, что ряд абсолютно сходится при |x| < R и расходится при |x| > R.
Из теоремы следует, что имеется интервал (–R; R) такой, что внутри этого интервала ряд (1.4) сходится абсолютно, а вне этого интервала ряд расходится (рис. 1). При x = ± R ряд может сходиться абсолютно или условно, может расходиться. Этот вопрос решается индивидуально для каждого конкретного ряда.

Рисунок 1

Одним из способов нахождения радиуса сходимости является исследование степенного ряда на абсолютную сходимость по признаку Даламбера. Найдем предел:

Пусть существует , обозначим этот предел , тогда .
Если < 1, или |x| < R, то ряд (1.4) сходится абсолютно. Если > 1, или |x| > R, то ряд (1.4) расходится. Если = 1 или x = ± R, ряд может как сходиться, так и расходиться.
Свойства степенных рядов запишем в виде следующих теорем.
Теорема 1. Пусть степенной ряд (1.4) имеет радиус сходимости R > 0. Тогда ряды, полученные из (1.4) почленным дифференцированием и интегрированием имеют тот же радиус сходимости.
Теорема 2. Степенной ряд (1.4) в каждой точке его интервала сходимости обладает следующими свойствами:
– его сумма является непрерывной функцией;
– его можно почленно дифференцировать и интегрировать, то есть, если S(x) = a_nxⁿ, то
(n + 1)a_n+1xⁿ = S ^'(x) ­ ­ ­ и ­ ­ ­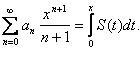
Путь дана бесконечно дифференцируемая в точке х = а функция f (x). При некоторых условиях ее можно представить в виде степенного ряда, который называется рядом Тейлора:

(1.5)

В частном случае, при а = 0 ряд (1.5) принимает вид:

Этот ряд называется рядом Маклорена для функции f (x).
Приведем разложение в степенные ряды основных элементарных функций.
На всей числовой оси справедливы разложения:

(1.6)

 

(1.7)

.

Следующие формулы справедливы в интервале (–1; 1):

,
,
.
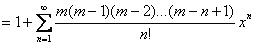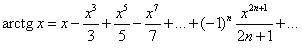Многие практически важные определенные интегралы не могут быть вычислены по формуле Ньютона-Лейбница, так как первообразная не всегда выражается в элементарных функциях. Однако если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости этого ряда, то этот ряд можно почленно проинтегрировать, а полученный ряд вычислить с наперед заданной точностью.

Содержание типового расчета

1. Исследовать заданный числовой ряд на сходимость. Если он сходится, найти сумму ряда, исходя из определения, т.е. как предел частичных сумм.
2. С точностью ε = 10^–4 вычислить два интеграла. Для этого разложить подынтегральную функцию в степенной ряд и найти область его сходимости. Затем проинтегрировать его почленно и вычислить сумму полученного ряда с заданной точностью.