 |
|
Тригонометрический ряд Фурье.
Ряды Фурье.
Периодические функции и процессы.
Определение. Функция f (x), определенная на неограниченно множестве D, называется периодической, если существует число T ¹ 0 такое, что "х ∈ D выполняется условие
f (x ± T) = f (x), где (x ± T) ∈ D.
Наименьшее из таких чисел Т называется периодом функции f (x).
Простейшими периодическими функциями являются sin x, cos x. Их период равен 2π.
Свойства периодических функций.
1. Сумма, разность, произведение и частное периодических функций периода Т есть периодические функции периода Т.
2. Если функция f (x) имеет период Т, то функция f (ax) (a ¹ 0) имеет период  .
.
3. Определенный интеграл от периодической функции f (x) с периодом Т по любому отрезку длиной Т имеет одно и то же значение, т. е. для любого х справедливо равенство
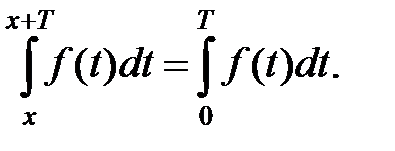
Определение. Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией
y = A sin (ωx + φ0), x ³ 0.
А – амплитуда колебания;
ω – частота колебания;
ωх + φ0 – фаза колебания;
φ0 – начальная фаза.
Функцию такого вида (и ее график) называют простой гармоникой. Основным периодом этой функции является 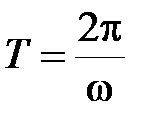 .
.
Используя формулы сложения тригонометрических функций, простую гармонику можно представить в виде

Отсюда видно, что простое гармоническое колебание описывается периодическими функциями sin ωx, cos ωx.
Сложное гармоническое колебание, возникающее в результате наложения конечного или бесконечного числа простых гармоник, так же описывается функциями вида sin ωx, cos ωx.
График суммы нескольких гармоник резко отличается от графика слагаемых гармоник.
Тригонометрический ряд Фурье.
Определение. Тригонометрическим рядом называется функциональный ряд вида
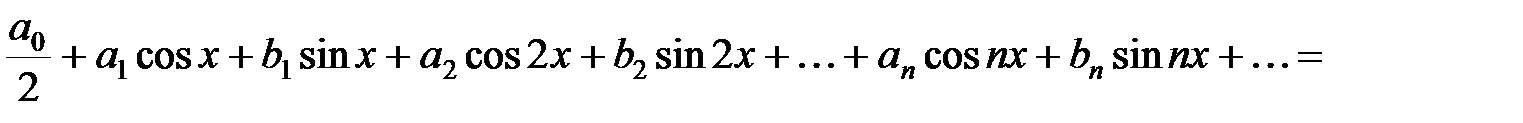
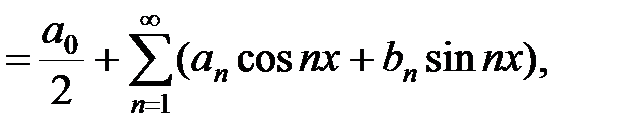 (14.1)
(14.1)
а числа а0, аn, bn – коэффициентами тригонометрического ряда.
Очевидно, что каждый член ряда (14.1) является периодической функцией с периодом 2π
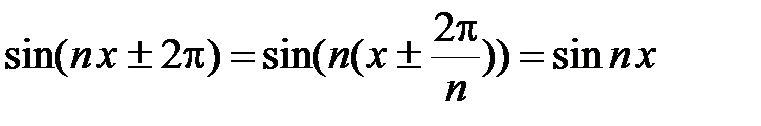 .
.
Следовательно, если ряд (14.1) сходится, то его сумма есть периодическая функция с периодом 2π.
Свободный член ряда записан в виде 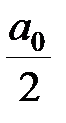 для единообразия получающихся в дальнейшем формул.
для единообразия получающихся в дальнейшем формул.
Теорема 14.1. (О единственности разложения в тригонометрический ряд). Если f (x) определена и интегрируема на [-π; π], разлагается в тригонометрический ряд
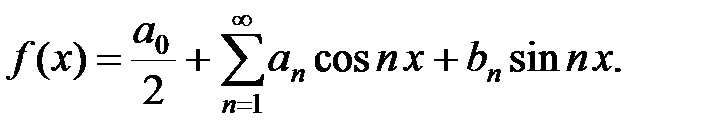 , (14.2)
, (14.2)
(т. е. является его суммой) который можно интегрировать почленно, то это разложение единственно и коэффициенты тригонометрического ряда в этом случае определяются формулами:
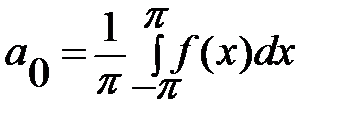 (14.3)
(14.3)
.  (14.4)
(14.4)
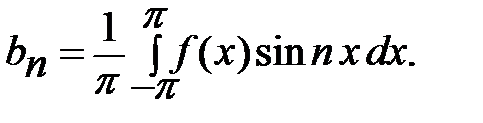 (14.5)
(14.5)
Определение. Пусть f (x) – функция определенная и интегрируемая на [-π; π]. Тогда коэффициенты а0, аn, bn, определяемые формулами (14.3) – (14.5) называются коэффициентами Фурье, а ряд (14.1) с этими коэффициентами называется рядом Фурье соответствующим функции f (x).
Разложение в ряд Фурье 2π – периодических функций.
Будем рассматривать функции f (x), имеющие период Т = 2π.
Теорема Дирихле (достаточное условие разложимости функции в ряд Фурье). Пусть 2π – периодичность f (x) на [- π; π] удовлетворяет условиям:
1) f (x) кусочно-непрерывная, т. е. непрерывна или имеет конечное число точек разрыва первого рода;
2) f (x) кусочно-монотонная, т. е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна. Тогда ряд Фурье функции f (x) сходится на [- π; π] и его сумма равна:
1) f (x) во всех точках непрерывности функции f (x), лежащих внутри [-π; π];
2) 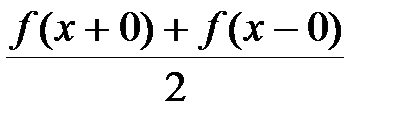 во всех точках разрыва;
во всех точках разрыва;
3)  на концах промежутка.
на концах промежутка.
Определение. Будем говорить, что функция F (x) определенная на всей числовой прямой и периодическая с Т = 2π является периодическим продолжением функции f (x), если на [- π; π] F (x) = f (x).
| - π |
| π |
| 2π |
| х |
| у |
Теорема Дирихле справедлива и для периодического продолжения функции f (x).