Главная | Обратная связь

Энергии для замкнутой системы материальных точек

 

В предыдущей главе мы познакомились с понятиями кинетической и потенциальной энергии для специального и относительно простого типа движения — движения одной материальной точки под действием заданной силы (движение в постоянном силовом поле). Теперь мы познакомимся с тем, как формулируется закон сохранения энергии для более сложного типа движения — движения многих взаимодействующих тел, образующих замкнутую систему.

Начнем с рассмотрения простейшей системы тел — системы, состоящей всего из двух материальных точек, а силу взаимодействия между ними будем полагать потенциальной и зависящей лишь от r = r₁— r₂. Эта оговорка весьма существенна. Например, сила взаимодействия между заряженными частицами, вообще говоря, непотенциальна и зависит от их скоростей, сила взаимодействия между двумя диполями, даже будучи потенциальной, зависит от ориентации частиц в пространстве и т. д. Запишем уравнения

движения рассматриваемых материальных точек в некоторой инерциальной системе координат:

 

 

где по-прежнему r₁ и r₂ — радиусы-векторы рассматриваемых материальных точек, v₁,v₂ — их скорости, m₁ и m₂ — их массы, a F₁₂, F₂₁ — силы, с которыми они действуют друг на друга. Мы предполагаем теперь, что наряду с силами F₁₂ и F₂₁ на тела действуют еще внешние, как говорят, сторонние, силы F₁ и F₂ (т. е., рассматриваемая система тел не является замкнутой).

Умножим обе части первого из уравнений (6.14) на бесконечно малое перемещение первого тела dr₁, умножим обе части второго уравнения на dr₂ и затем сложим левые и правые части полученных таким образом соотношений. С учетом того, что

 

получаем:

 

 

 

где dr = dr₂ - dr₁,

и, поскольку dr₁/dt = v₁, dr₂/dt = v₂, отсюда следует

 

 

(6.15)

 

Определим понятие потенциальной энергии взаимодействия:

потенциальной энергией взаимодействия и₁₂(r) между материальными точками 1 и 2, находящимися на расстоянии r друг от друга, называется работа, совершаемая силой взаимодействия при удалении одной из них от другой с расстояния r в бесконечность, т. е.

 

u₁₂(r) =A_B3(r->oo). (6.16)

 

Определение конкретного выражения для u₁₂(r) сводится, как мы видим, к вычислению А_вз(r —> оо) для конкретной силы взаимодействия F₂₁, и в следующем параграфе мы покажем в качестве примера, как находится потенциальная энергия гравитационного взаимодействия. Бесконечность в (6.16) принято вводить для определенности; разумеется, при вычислении сил либо работы на конечном участке пути потенциальная энергия, как и

в постоянном силовом поле (гл. 5), определена с точностью до константы.

Если силы взаимодействия между материальными точками являются потенциальными, то работа не зависит от пути. Это, в частности, справедливо для важного частного случая центральных сил:

F₁₂ = F₁₂ (r/r); r = r₁ - r₂. (6.17)

 

Здесь r /r — единичный вектор, так называемый орт направления. Закон взаимодействия (6.17) никогда не бывает справедлив в точности, но очень во многих случаях используется как достаточно хорошее приближение к реальности.

Подчеркнем одно отличие потенциальной энергии взаимодействия между двумя материальными точками u₁₂ от потенциальной энергии одной материальной точки в постоянном силовом поле U(r), о которой шла речь в гл. 5. Потенциальная энергия взаимодействия двух материальных точек зависит только от расстояния между ними r — если, конечно, не вступают в игру ориентационные координаты, скажем, направление дипольных моментов частиц (о чем мы будем говорить в следующем разделе курса). Чтобы подчеркнуть это различие, потенциальную энергию взаимодействия двух

материальных точек называют обычно просто энергией взаимодействия, и мы так и будем ее называть в дальнейшем.

Из соотношения (6.15) следует связь между работой и приращением кинетической энергии при бесконечно малых перемещениях:

 

dT = δA_B3 + δA_BH. (6.18)

 

Здесь Т обозначает суммарную кинетическую энергию рассматриваемых материальных точек —

 

Т = m₁v²(г₁)/2 + m₂v²(г₂)/2,

 

δА_ВЗ = F₂₁ dr

обозначает бесконечно малую работу силы F₂₁, a

 

δA_BH = F₁dr₁+ F₂ dr₂

 

— бесконечно малую работу внешних сил.

Из определения энергии взаимодействия (6.16) получаем

 

du₁₂ = u₁₂(r + dr) – u₁₂(r) = A_B3(r + dr ->> oo) - A_B3(r -> oo). (6.19)

 

Ввиду нашего предположения о потенциальности сил взаимодействия, ра-

работа их от пути не зависит. Поэтому работу Авз(r —> оо) при удалении тела

с расстояния r на бесконечность можно совершить, удалив сначала тело по

произвольным траекториям на расстояние r + dr, а затем удалив его из этого

положения на бесконечность, т. е.

 

Авз(r —>> оо) = Авз(r —>> r + dr) + A_B3(r + dr —>> oo).

 

Подставляя полученный результат в (6.19), получаем

 

du₁₂ = -А_вз(r -> r + dr) = -δА_ВЗ, (6.20)

 

как следствие, соотношение (6.18) принимает вид

 

dT = - du₁₂ + δА_ВH,

 

После перегруппировки слагаемых последнее равенство можно представить как

 

d(T + u₁₂) = δA_BH. (6.21)

 

Если внешние силы отсутствуют, то и δА_вн = 0. В этом случае из (6.21) следует, что для замкнутой системы где Е обозначает полную энергию замкнутой системы из двух

материальных точек. В этом случае из (6.21) следует, что полная энергия замкнутой

системы двух тел остается при их движении постоянной:

 

Е = (m₁v_l²/2) + (m₂v₂²/2) + u₁₂ = const. (6.22)

 

Следует отметить, что утверждение, выраженное формулой (6.22), имеет характер намного более общий, нежели наш вывод, представляющий по сути частный пример. Значение константы (инварианта, интеграла движения) в (6.22) может быть различным, и оно определяется значениями кинетической энергии и энергии взаимодействия в некоторый (например, начальный) момент времени.

Сформулируем теперь закон сохранения энергии для общего случая, когда замкнутая система состоит не из двух, а из произвольного числа N взаимодействующих материальных точек. Фомулировка является обобщениемформулы (6.22), а именно:

при движении N материальных точек в замкнутой системе сохраняется ее полная энергия, равная сумме кинетических энергий всех материальных точек и всех попарных потенциальных энергий взаимодействия между ними:

 

(6.23)

 

где суммирование по индексам l и m проводится от 1 до N, и во второй сумме при этом содержатся только слагаемые с l> m, чтобы не учитывать дважды вклады от энергии взаимодействия каждой из пар материальных точек. Кроме того, для того чтобы сделать запись формулы более компактной, мы ввели обозначения: v(r_l) = v_l и u(|r_l - r_m|) =

= u_lm. Так для замкнутой системы из трех материальных точек (например, тройная звезда) закон сохранения (6.16) запишется в виде (рис. 6.5):

 

 

 

 

 

Сколь ни естественно выглядит формула (6.23) в качестве обобщения закона (6.22), применимость ее ограничена важным дополнительным условием. Мы предположили, что имеет место принцип суперпозиции сил. В случае их потенциальности это означает аддитивность потенциальной энергии:

 

 

 

Нарушения этих условий не столь уж и редки (например, взаимодействие

нуклонов в ядре не есть сумма их попарных взаимодействий друг с другом). Но в классической механике, пока и поскольку мы не обращаемся к космическим масштабам либо нелинейным свойствам сплошной среды, закон сохранения энергии в форме (6.23) имеет достаточно широкую область применимости. Напомним, что мы показали на примере системы из двух материальных точек, что бесконечно малое изменение их полной энергии dE равно бесконечно малой работе внешних сил δА_ви. Обобщая это на случай произвольного числа материальных точек, мы имеем, следовательно,

равенство

dE = δA_вн

Применительно к конечным изменениям энергии оно означает, что изменение полной энергии системы материальных точек равно работе внешних сил. При этом всю потенциальную энергию частиц, составляющих нашу систему, вместе с кинетической энергией в ц-системе, зачастую удобно интерпретировать как внутреннюю энергию, тем самым представляя систему частиц в качестве одного макроскопического тела.

С учетом теоремы Кенига (6.13) энергию Е системы N материальных точек в любой инерциальной системе координат можно записать в виде

 

 

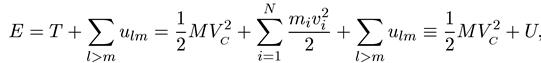
где внутренняя энергия U равна

 

 

Так как v_i — скорости относительно центра масс, то внутренняя энергия системы не зависит от скорости ее движения как целого и определяется только ее собственными, внутреннеми свойствами — внутренними степенями свободы. Мы рассмотрим данный вопрос на должном уровне в разделе, посвященном термодинамике.

Если система как целое покоится (Vc = 0), то Е = U — вся энергия системы равна ее внутренней энергии, соответственно, dU = δA_BH.

 

 

Закон сохранения импульса:

 

d( mV) = 0 ,

или

S mV = 0

радиус вектор частицы можно представить в трехмерном случае в виде

r = xi + yj + zk

 

уравнения движения в проекциях на оси координат

m₁ d²x / dt² = F_x

m₁ d²y / dt² = F_y

m₁ d²z / dt² = F_z

 

вектор силы в трехмерном представлении

F = F_xi + F_yj + F_zk

 

При задании начальных условий задача описания движения становится корректной и позволяет однозначно определить положение(координаты) и скорости(импульс) для частицы или системы частиц

 

t = 0, x = 0 …

t = 0, v = v _0i …

 

исходя из уравнения Ньютона (второй закон) можно получить выражение для работы, совершаемой в системе по перемещению материальных тел

 

m₁ d²x / dt² = F [ m dv/dt = F

 

Домножая последнее выражение на скорость, получим

 

mvdv/dt = vF

 

Внося скорость под знак дифференциала, имеем

 

d(mv²/ 2 ) / dt = vF = Fdx / dt

 

Что эквивалентно выражению

 

d (mv²/ 2 ) = Fdx – работа

 

Если F = 0, то

 

d (mv²/ 2 ) = 0,

 

то есть кинетическая энергия сохраняется.

Работа

 

dA = Fdx (d - изменение )

 

Учитывая, что сила и перемещение вектора, произведение векторов скалярное, для модуля можно записать

 

Fdx = Fdx cosa

Закон сохранения энергии:

Для консервативных сил(потенциальных) выражение для силы имеет вид

 

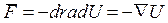
Или

 

тогда

 

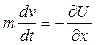
Домножая на скорость, получим

 

 

Внося скорость под знак дифференциала имеем

 

 

Преобразуем правую часть уравнения с учетом перемены порядка дифференцирования

 

 

Объединяя производные

 

 

Или

 

 

-закон сохранения энергии, где

 

E - полная энергия;

 

mV ² / 2 - кинетическая энергия;

 

U - потенциальная энергия.

 

-условие постоянства дифференцируемой функции-полной энергии

 

Построим график зависимости потенциальной энергии U((x) от x и отметим на рисунке уровень с энергией E

 

 

U

x

x₁ , x₂ , x₄

 

 

Рис. 20.1. Потенциальная энергия частицы и действующая на нее консервативная сила

 

 

Пусть U = E в т. x₁ , x₂ , x₄ , при этом V = 0,

x₁ , x₂ , x₄ - точки остановки.

 

при -

при 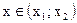- барьер, в этой области находятся недопустимые значения.

при - область периодических колебаний; частицы в этой области стремятся занять минимальное значение энергии, то есть достичь т.x₃, или

- потенциальная яма.

точка равновесия x = x_p

F>0

F<0

F=0

 

 

 

Рис. 5.11

1. Если при малом нарушении равновесия возникает отклик в виде возвращающей силы, материальная точка не может уйти из точки равновесия x₀ слишком далеко (рис. 5.11 а). Само воздействие может заключаться либо в перемещении точечной массы в некоторую точку х ≠ x₀, либо в придании ей некоторой начальной скорости. Она, однако, останется в некоторой окрестности точки х₀, если выполнено условие

 

dU/dx > 0 при х > 0; dU/dx < 0 при х < 0,

 

Иными словами, устойчивому равновесию отвечает минимум потенциальной энергии, что в одномерной задаче эквивалентно условиям: