Главная | Обратная связь

Числовые характеристики функции случайного аргумента.

Вопрос 1

 

Одномерные:

Случайной величиной X называется числовая функция, определенная на пространстве элементарных событий , которая каждому элементарному событию ставит в соответствие определенное число.

Законом распределения случайной величины называется любое правило, указывающее вероятности отдельных значений случайной величины или множества этих значений.

Различают два типа СВ: • дискретные; • непрерывные.

Дискретной СВ называется такая величина, число всевозможных значений которой является счётным множеством (конечным или бесконечным).

Непрерывной СВ называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал (конечный или бесконечный).

Многомерные:

 

Вопрос 2

Функцией распределения случайной величины X называется функция , которая для любого вещественного числа х равна вероятности события (X <х): .

Свойства функции распределения F(x):

1.

2. — неубывающая непрерывная функция.

3. .

4. 0<F(x)<1

 

Функцией распределения случайного вектора или совместным распределением случайных величин называется функция, определенная равенством

,

где .

1. 0£ F(x₁,…,x_m)£ 1;

2. F(x₁,…,x_m) не убывает по каждому аргументу;

3. ;

4.

Вопрос 3

Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности:
M(X) = x₁p₁ + x₂p₂ + ... + x_np_n

Свойства математического ожидания.
1) Математическое ожидание постоянной величины равно самой величине:
М(С) = С
2) Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С·М(Х)
3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
М(Х₁ + Х₂ + …+ Х_n) = М(Х₁) + М(Х₂) + ... + М(Х_n)
4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
М(Х₁ · Х₂ · ... · Х_n) = М(Х₁) · М(Х₂) · ... · М(Х_n)

Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
D(X) = (x₁ - M(X))²p₁ + (x₂ - M(X))²p₂ + ... + (x_n- M(X))²p_n = x²₁p₁ + x²₂p₂ + ... + x²_np_n - [M(X)]²

Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю: D(С) = 0
2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х)
3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х₁ ± Х₂ ± ... ± Х_n) = D(Х₁) + D(Х₂) + ... + D(Х_n)

Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)

Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.

Коэффициент вариации случайной величины - это относительная мера вариации.
V(X) = |σ(X)/M(X)| · 100%

Асимметрия (коэффициент асимметрии) случайной величины (и дискретной, и непрерывной) As(X) - величина, характеризующая степень асимметрии распределения относительно математического ожидания. Коэффициент асимметрии дискретной случайной величины вычисляется по формуле:
As(X) = [(x₁-M(X))³p₁ + (x₂-M(X))³p₂ + ... + (x_n-M(X))³p_n]/σ³
Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находятся левее математического ожидания, и наоборот, если As(X)>0, то правее.

Эксцесс (коэффициент эксцесса) случайной величины (и дискретной, и непрерывной) Ex(X) - величина, характеризующая степень островершинности или плосковершинности распределения, т.е. степень так называемого «выпада». Коэффициент эксцесса дискретной случайной величины вычисляется по формуле:
Ex(X) = [(x₁-M(X))⁴p₁ + (x₂-M(X))⁴p₂ + ... + (x_n-M(X))⁴p_n]/σ⁴ - 3

 

Вопрос 4

Случайная величина, принимающая п ( ) значений х₁, х₂,..., x_n с вероятностями р_i=1/п, называется случайной величиной, распределенной по дискретному равномерному закону. На рис. 2.3 рассматриваемая случайная величина (дляn=6) представлена в графической форме. Случайная величина, распределенная по дискретному равномерному закону, является моделью событий с равновероятными исходами (см. пример с бросанием игральной кости)

.

Случайная величина, принимающая два значения: 0 и 1 с вероятностями q=1-р и р, соответственно(0<р<1), называется случайной величиной, распределенной по закону Бернулли спараметром p. Случайная величина, распределенная по закону Бернулли - это удачная модель для описания многих конкретных испытаний, имеющих два исхода (наиболее известный пример - бросание правильной монеты; здесь p=q=1/2), в том числе и в биологии: присутствие или отсутствие некоторого признака: пол родившегося цыпленка, цвет цветка и т. д..

Случайная величина , принимающая п+1 значение 0, 1, 2,..., п, с вероятностями

где i=0, 1, 2,..., n, q=1-р, 0<p<1, называется биноминально распределенной случайной величиной, а п и р - параметрами распределения.

На рис. 2.4 биномиальная случайная величина представлена в графической форме. Пример использования биномиальной случайной величины дан в 2.1.

Рис. 2.4. Распределение вероятностей биномиально

распределенной случайной величины для n=10 и p=0.2.

 

Заметим также, что случайная величина, распределенная по закону Бернулли, является частным случаем биномиальной случайной величины для n=1.

Случайная величина , принимающая счетное множество значений 0, 1, 2,..., с вероятностями

где i=0, 1, 2, ..., 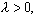называется случайной величиной, распределенной по закону Пуассона. Величина называется параметром распределения Пуассона.

На рис. 2.5 случайная величина, распределенная по закону Пуассона, представлена в графической форме. Случайная величина, распределенная по закону Пуассона, служит моделью эксперимента, связанного с определением численности бактерий в единице объема, или численности животных на единицу площади, и других подобных экспериментов.

Вопрос 5

Пусть некоторая случайная величина Х подвергается детерминированному преобразованию j, в результате которого получается величина У. Рассмотрим задачу определения числовых характеристик и закона распределения получаемой в результате преобразования случайной величины У.

Числовые характеристики функции случайного аргумента.

Рассмотрим случайную величину Y, зависящую функционально от случайной величины X с известным законом распределения F(x): Y=φ(X).

Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид:

Xi	x1	x2	…	xn
pi	p1	p2	…	pn

Определяем вероятности появления различных значений случайной величины У

φ(X)i	φ(x1)	φ(x2)	…	φ(xn)
pi	p1	p2	…	pn

 

Тогда математическое ожидание случайной величины Y определяется так:

(9.1)

Если случайная величина X непрерывна и имеет плотность распределения f(x), то заменяя в формуле (9.1) вероятности p_i элементом вероятностиf(x)dx, а сумму – интегралом, получаем:

. (9.2)

Для смешанной случайной величины выражение для математического ожидания преобразуется к виду:

(9.3)

Соотношения (9.1), (9.2) и (9.3) – общее понятие математического ожидания, позволяющее вычислить математическое ожидание для неслучайных функций случайного аргумента. Например, дисперсия случайной величины Y=φ(x) определяется так:

Величину M[φ(x)] рассчитываем в соответствии с (9.1)-(9.3). Для определения математического ожидания квадрата φ(х) воспользуемся следующими соотношениями:

. (9.4)

Таким образом, для нахождения числовых характеристик функции Y=φ(x) достаточно знать закон распределения ее аргумента.

Вопрос 6