Главная | Обратная связь

Тема №8 Формула Бернулли

Опыты a₁, a₂,… называются независимыми, если любая комбинация их исходов является совокупностью независимых событий.

В вероятностной схеме Бернулли рассматривается последовательность n независимых опытов a₁, a₂,…, a_n, в каждом из которых некоторое событие А может наступить с одной и той же вероятностью р = р(А). Условно это событие рассматривается как успех, а его ненаступление (событие ) – как неудача. Вероятность неудачи в каждом опыте равна: q = 1 – p .

Пусть для заданного целого числа k (0 £ k £ n) P_n(k) обозначает вероятность того, что в n опытах успех наступит ровно k раз. Имеет место формула Бернулли:

P_n(k) = p^k q^n-k. (1)

Вероятности P_n(k) (k = 0,1,…,n) называются биномиальными в силу того, что правая часть формулы (1) представляет собой общий член разложения бинома Ньютона:

. (2)

Так как p+q=1, то из формулы (2) следует, что сумма всех биномиальных вероятностей равна 1:

.

Пример 1. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,8 и не зависит от номера выстрела. Требуется найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.

Решение. В этом примере n = 5, р = 0,8 и k = 2; по формуле Бернулли находим: .

Пример 2. 2 равносильных шахматиста играют ряд партий, причем ничьи в счет не идут. Что более вероятно в счете: ( 1 : 1), ил (2 : 2), или (3 : 3) и т.д.?

Решение. Найдем по формуле Бернулли вероятность того, что в 2n результативных партиях один из шахматистов выиграет n партий, т.е. счет будет n : n. Принимая во внимание, что p = q = , имеем:

.

Преобразуем полученное выражение с целью найти связь между P_2n(n) и P_2n+2(n+1):

 

.

Из полученного соотношения

(3)

видно, что счет (n : n) более вероятен, чем (n + 1 : n + 1). Расчеты по формуле Бернулли показывают, что последовательности событий (1 : 1), (2 : 2), (3 : 3), (4 : 4), … соответствует последовательности вероятностей

, , , , …. .

 

То число успехов k₀, которому при заданном n соответствует максимальная биномиальная вероятность P_n(k₀), называется наиболее вероятным числом успехов.

Для нахождения наиболее вероятного числа успехов k₀ по заданным n и р можно воспользоваться неравенствами

np – q £ k₀ £ np + p (4)

или правилом: если число np + p не целое, то k₀ равно целой части этого числа

(k₀ = [np + p]); если же np + p целое, то k₀ имеет два значения и р.

Пример 3. Найдите наиболее вероятное число попаданий в мишень при 5 выстрелах, используя условие примера 1, и соответствующую этому числу вероятность.

Решение. Так как np + p = 5 × 0,8 = 4,8 не целое, то k₀ = [4,8] = 4; вероятность Р₅(4) находим по формуле Бернулли:

.

Пример 4. Найдите наиболее вероятное число выпаданий герба при 25 бросаниях монеты.

Решение. В этом примере n = 25, p = 0,5. Число np + p = 25 ×0,5+0,5=13 –целое, поэтому и .

Пусть Р_n (k₁ £ k £ k₂) – вероятность того, что в n опытах схемы Бернулли успех наступит от k₁ до k₂ раз (0 £ k₁ £ k £ n ). Тогда имеет место формула

Р_n (k₁ £ k £ k₂) = ; (5)

вероятность Р_n (1 £ k £ n) того, что в n опытах успех наступит хотя бы один раз, равна:

Р_n (1 £ k £ n)= 1 – qⁿ. (6)

 

Пример 5. Монета брошена 10 раз. Найдите вероятность того, что герб выпадет: а) от 4 до 6 раз; б) хотя бы один раз.

Решение. А) По формуле (5) при n = 10, k₁ = 4, k₂ = 6, p = q = 0,5 получим:

Р₁₀ (4 £ k £ 6) = Р₁₀ (4) + Р₁₀ (5) + Р₁₀ (6) = .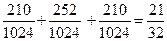

б) По формуле (6) Р₁₀ (1 £ k £ 10) = .

Пример 6. Какое минимальное число опытов достаточно провести, чтобы с вероятностью, не меньшей, чем a (0 < a < 1), можно было бы ожидать наступления успеха хотя бы один раз, если вероятность успеха в одном опыте равна р?

Решение. Потребуем, чтобы вероятность наступления успеха хотя бы один раз в n опытах (см. формулу (6)) была не меньше чем a:

1 – qⁿ ³ a, или 1 – (1 – р)ⁿ ³ a.

Решив полученное равенство относительно n, получаем неравенство

.

Отсюда заключаем, что минимальное число опытов n₀, удовлетворяющее условию примера, равно:

. (7)

В частности, если р = 0,02 и a = 0,98, то формула (7) дает n₀ = 80.

 

Пусть производится n независимых опытов, каждый из которых имеет m (m ³ 2) попарно несовместных и единственно возможных исходов А₁, А₂,…, А_m с вероятностями р₁= р(А),…,р_m = (A_m), одинаковыми во всех опытах (имеется в виду, что р₁+р₂+…+ р_m=1). Для произвольных целых неотрицательных чисел k₁, k₂,…,k_m (k₁+ k₂+…+k_m = n) обозначим через P_n (k₁, k₂,…,k_m) вероятность того, что в n опытах исход А₁ наступит k₁ раз, исход А₂ - k₂ раз и т.д., исход A_m - k_m раз. Тогда справедлива формула

P_n (k₁, k₂,…,k_m) = , (8)

которая является обобщением формулы Бернулли на случай, когда каждый из независимых опытов a₁, a₂,…, a_n имеет m исходов (m ³ 2).

Вероятности P_n (k₁, k₂,…,k_m), соответствующие всевозможным наборам целых неотрицательных чисел k₁, k₂,…,k_m с условием k₁+ k₂+…+k_m = n назовем полиномиальными, ввиду того что выражение, стоящее в правой части формулы (8), представляет собой общий член разложения (р₁+р₂+…+ р_m)ⁿ по полиномиальной формуле .

Вывод формулы (8) аналогичен выводу формулы Бернулли.

Пусть событие В означает: в n независимых опытах событие А_i наступит k₁ раз, событие А₂ - k₂ раз и т.д., событие A_m - k_m раз. Тогда P_n (k₁, k₂,…,k_m) = р(В). Каждый вариант реализации события В можно интерпретировать как строку длины n, составленную из символов А₁, А₂,…, А_m , в которой А_i повторяется k₁ раз, А₂ - k₂ раз и т.д., A_m - k_m раз. Количество N таких строк равно числу размещений состава (k₁, k₂,…,k_m), т.е.

;

вероятность же каждого варианта равна . Отсюда по правилу сложения вероятностей имеем (8).

 

Пример 7. Мишень состоит из 3 попарно непересекающихся зон. При одном выстреле по мишени вероятность попадания в первую зону для данного стрелка равна 0,5. Для второй и третьей зон эта вероятность равна соответственно 0,3 и 0,2. Стрелок произвел 6 выстрелов по мишени. Найдите вероятность того, что при этом окажется 3 попадания в первую зону, 2 попадания во вторую и одно попадание в третью зону.

Решение. В этом примере n = 6, k₁ = 3, k₂ = 2, k₃ = 1, p₁ = 0,5, p₂ = 0,3 и p₃ = 0,2. Подставляя эти данные в формулу (8), получаем искомую вероятность:

.