Главная | Обратная связь

Тема №11 Функция распределения случайной величины

 

На практике для задания случайных величин общего вида обычно используется функция распределения.

Вероятность того, что случайная величина х примет определенное значение х₀ , выражается через функцию распределения по формуле

р (х = х₀) = F(x₀ +0) – F(x₀). (3)

В частности, если в точке х = х₀ функция F(x) непрерывна, то

р (х = х₀) =0.

Случайная величина х с распределением р(А) называется дискретной, если на числовой прямой существует конечное или счетное множество W, такое, что р(W,) = 1.

Пусть W = {x₁, x₂,…} и p_i = p({x_i}) = p(x = x_i), i = 1,2,….Тогда для любого борелевского множества А вероятность р(А) определяется однозначно формулой

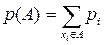. (4)

Положив в этой формуле А = {x_i / x_i < x}, x Î R, получим формулу для функции распределения F(x) дискретной случайной величины х:

F(x) = p(x < x) = . (5)

График функции F(x) представляет собой ступенчатую линию. Скачки функции F(x) в точках х = х₁, х₂ …(x₁<x₂<…) равны соответствующим вероятностям р₁, p₂, ….

Пример 1. Найдите функцию распределения

дискретной случайной величины х из примера 1§ 13.

Используя функцию распределения, вычислите

вероятности событий: х < 3, 1 £ x < 4, 1 £ x £ 3.

F(x)

0 х1 х2 х3 х4 х

Решение. Используя данные из таблицы,

полученной в § 13, и формулу (5), получим

функцию распределения:

 

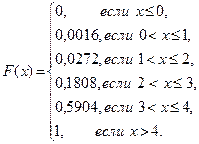
По формуле (1) Р(x < 3) = F(3) = 0,1808; по формуле (2)

р(1 £ x < 4) = F (4) – F(1) = 0,5904 – 0,0016 = 0,5888;

p (1 £ x £ 3) = p ( 1 £ x <3) + p(x = 3) = F(3) – F(1) + F(3+0) – F(3) =

= F(3+0) – F(1) = 0,5904 – 0,0016 = 0,5888.

Пример 2. Дана функция

Является ли функция F(x) функцией распределения некоторой случайной величины? В случае положительного ответа найдите . Построить график функции F(x).

Решение. Для того чтобы наперед заданная функция F(x) являлась функцией распределения некоторой случайной величины х, необходимо и достаточно выполнение следующих условий (характеристических свойств функции распределения):

1. F(x) – неубывающая функция.

2. , .

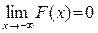3. При любом х Î R F(x – 0) = F(x).

Для заданной функции F(x) выполнение

этих условий очевидно. Значит,

F(x) – функция распределения.

Вероятность вычисляем по

формуле (2):

.

График функции F(x) представлен на рисунке 13.

Пример 3. Пусть F₁(x) и F₂(x) – функции распределения случайных величин х₁ и х₂ соответственно, а₁ и а₂ – неотрицательные числа, сумма которых равна 1.

Доказать, что F(x) = a₁F₁(x) + a₂F₂(x) является функцией распределения некоторой случайной величины х.

Решение. 1) Так как F₁(x) и F₂(x) – неубывающие функции и а₁ ³ 0, а₂ ³ 0, то a₁F₁(x) и a₂F₂(x) - неубывающие, следовательно, их сумма F(x) тоже неубывающая.

2) ;

.

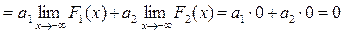3) При любом х Î R F(x - 0) = a₁F₁(x - 0) + a₂F₂(x - 0)= a₁F₁(x) + a₂F₂(x) = F(x).

Пример 4. Дана функция

Является ли F(x) функцией распределения случайной величины?

Решение. Легко заметить, что F(1) = 0,2 > 0,11 = F(1,1). Следовательно, F(x) не является неубывающей, а значит, не является функцией распределения случайной величины. Заметим, что остальные два свойства для данной функции справедливы.