Главная | Обратная связь

Случайные события и их вероятности

Пермский национальный исследовательский

Политехнический университет

Учебное пособие для выполнения практических и контрольных работ по "Математике"

"Теория вероятностей"

 

Пермь 2013

 

 

"Теория вероятностей": Учебное пособие для выполнения практических и контрольных работ по курсу "Математика", "Элементы высшей математики" для студентов всех специальностей среднего профессионального образования.

 

Разработал: преподаватель А.С. Ремизова

 

Учебное пособие представляет собой руководство к решению задач раздела "Теория вероятностей" курса "Математика" и "Элементы высшей математики" для студентов специальностей СПО на базе среднего (полного) общего образования.

Основное назначение пособия – помочь студенту самостоятельно, без помощи преподавателя изучить приемы решения основных задач, закрепить полученные навыки при выполнении контрольной работы и подготовиться к зачету по данному разделу.

Введение

 

Отличительной чертой современного общества является его высокая информативность, на основе которой можно достигнуть эффективного управления как отдельными объектами: предприятиями, фирмами, отраслями экономики, биологическими системами и организмами, так и различными процессами, протекающими в политической, общественной, социальной жизни. Чтобы достичь успеха в принятии наиболее правильного решения, не достаточно просто владеть полной информацией об объекте управления, необходимо хорошо ориентироваться в мире информации, использовать научные методы оценки случайностей и выявления взаимосвязей и активно действовать, опираясь на скрытые специфические закономерности. Искусство управления определяется принятием интегрированных решений, учитывающих разносторонние факторы, которые изменяются с какой-то долей случайности, неопределенности и закономерности развития различных событий.

Случайные факторы лежат в основе событий, происходящих в окружающей среде, в экономике, политике, в социальной и общественной жизни, они определяют течение любого процесса массового обслуживания, окружают нас повсюду. Например, срок бесперебойной службы купленного в магазине холодильника носит случайный характер, но можно выявить зависимость увеличения этого срока от фирмы-производителя или от качества комплектующих деталей. Случайными являются и изменения погоды, ураганы, тайфуны, землетрясения, катастрофы, банкротство фирм, однако многие из этих событий люди научились предугадывать с достаточно большой точностью. Фундаментом для научного подхода к поиску ответов на вопросы подобного рода является теория вероятностей. Вероятностные законы, теоремы и выводы являются теоретической основой для методовматематической статистики, эконометрики, прогнозирования.

Научно обоснованные выводы, прогнозы и методики планирования хозяйственной деятельности, базирующиеся на статистической обработке информации, предопределяют неразрывную связь фундаментальной теории и практики. Дисциплина «Теория вероятностей и математическая статистика» приобрела в настоящее время практический характер. Модели исследования закономерностей, разрабатываемые специалистами в разных областях науки, техники, экономики, используют методы стохастического (вероятностного) анализа изучаемых процессов. Внедрение современных информационных технологий позволяет применять эти методы для решения широкого круга задач.

Теория вероятностей возникла в середине XVII века в связи с задачами расчета шансов выигрыша игроков в азартных играх. Французский математик Паскаль впервые использовал классическое понятие вероятности. Однако только в двадцатом веке теория вероятностей превратилась в стройную математическую дисциплину, основанную на строгих математических доказательствах.

 

Случайные события и их вероятности

1. Случайные события

Теория вероятностей— это раздел математики изучающий закономерности массовых случайных событий.

Случайным называется событие, наступление которого нельзя гарантировать. Случайность того или иного события определяется множеством причин, которые существуют объективно, но учесть их все, а также степень их влияния на изучаемое событие, невозможно. К таким случайным событиям относятся: выпадание того или иного числа при бросании игральной кости, выигрыш в лотереи, коли­чество больных, записавшихся на прием к врачу и т.п.

И хотя в каждом конкретном случае трудно предсказать исход испытания, при достаточно большом числе наблюдений можно установить наличие некоторой закономерности. Подбрасывая монету, можно заметить, что число выпадания орла и решки примерно одинаково, а при бросании игральной кости различные грани также появляются, примерно одинаково. Это говорит о том, что случайным явлениям присущи свои закономерности, но они проявляются лишь при большом количестве испытаний. Правильность этого подтверждает закон больших чисел, который лежит в основе теории вероятностей.

Рассмотрим основные термины и понятия теории вероятностей.

Испытанием называется совокупность условий, при которых может произойти данное случайное событие.

Событие - это факт, который при осуществлении определенных условий может произойти или нет. События обозначают большими буквами латинского алфавита А, В, С...

Например,событие А - рождение мальчика, событие В – выигрыш в лотерее, событие С - выпадение цифры 4 при бросании игральной кости.

События бывают достоверные, невозможные и случайные.

Достоверное событие — это событие, которое в результате испытания непременно должно произойти.

Например,если на игральной кости на всех шести гранях. нанести цифру 1, тогда выпадение цифры 1, при бросании кости, есть событие достоверное.

Невозможное событие - это событие, которое в результате испытания не может произойти.

Например,в ранее рассмотренном примере — это выпадение любой цифры, кроме 1.

Случайное событие — это событие, которое при испытаниях может произойти или не произойти. Те или иные события реализуются с различной возможностью.

Например,завтра днем ожидается дождь. В этом примере наступление дня является испытанием, а выпадение дождя - случайное событие.

События называются несовместными, если в результате данного испытания появление одного из них исключает появление другого.

Например,при бросании монеты выпадение одновременно орла и решки есть события несовместные.

События называются совместными, если в результате данного испытания появление одного из них не исключает появление другого.

Например,при игре в карты появление валета и масти пик — события совместные.

События называются равновозможными, если нет оснований считать, что одно из них происходит чаше, чем другое!

Например,выпадение любой грани игрального кубика есть равновозможные события.

События образуют полную группу событий, если в результате испытания обязательно произойдет хотя бы одно из них и любые два из них несовместны.

Например,при 10 выстрелах в мишень возможно от 0 до 10 попаданий. При бросании игрального кубика может выпасть цифра от 1 до 6. Эти события образуют полную группу.

События, входящие в полную группу попарно несовместных и равновозможных событий, называются исходами, или элементарными событиями. Согласно определению достоверного события, можно считать, что событие, состоящее в появлении одного, неважно какого, из событий полной группы, есть событие достоверное.

Например,при бросании одного игрального кубика выпадает число меньше семи. Это пример достоверного события.

Частным случаем событий, образующих полную группу, являются противоположные события.

Два несовместных события А и (читается «не А») называются противоположными, если в результате испытания одно из них должно обязательно произойти.

Например,если стипендия начисляется только при получении на экзамене хороших и отличных оценок, то события «стипендия» и «неудовлетворительная или удовлетворительная оценка» — противоположные.

Событие А называется благоприятствующим событию В, если появление события А влечет за собой появление события В.

Например,при бросании игрального кубика появлению нечетного числа благоприятствуют события, связанные с выпадением чисел 1,3 и 5.

 

2. Операции над событиями

 

Операции над событиями аналогичны операциям над множествами.

Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.

Сумма событий может быть обозначена знаками «+», «È», «или».

На рисунке 1 представлена геометрическая интерпретация с помощью диаграмм Эйлера-Венна. Сумме событий А + В будет соответствовать вся заштрихованная область.

рис.1

Область пересечения событий А и В соответствует совместным событиям, которые могут произойти одновременно. Аналогично для событий А, В и С имеются совместные события А и В; А и С; В и С; А и В и С, которые могут про изойти одновременно.

Например,в урне находятся белые, красные и синие шары. Возможны следующие события: А — вынут белый шар; В — вынут красный шар; С — вынут синий шар. Событие В + С означает, что произошло событие — вынут цветной шар или вынут не белый шар.

Произведением нескольких событий называется событие которое состоит в совместном наступлении всех этих событий в результате испытания.

Произведение событий может быть обозначено знаками «х», «∩», «и».

Геометрическая интерпретация произведения событий представлена на рис. 2.

 

рис.2

 

Произведением событий А и В будет заштрихованная область пересечения площадей А и В. А для трех событий А и В и С - общая площадь, одновременно входящая во все три события.

Например,пусть из колоды карт наугад извлекается карта. Событие А - вынута карта пиковой масти; В - вынут валет. Тогда событие А×В означает событие — вынут валет пик.

Разностью двух событий А-В называется событие, состоящее из исходов, входящих в А, но не входящих в В.

На рис. 3 представлена иллюстрация разности событий с помощью диаграмм Эйлера-Венна.

рис.3

Разностью двух событий А-В является заштрихованная область А без той части, которая входит в событие В. Разность между произведением событий А и В и событием С будет совместная площадь события А и события В без совместной с нею площадью события С.

Например,пусть при бросании игрального кубика событие А - появление четных чисел (2,4,6), а событие В - чисел-кратных 3, т.е. (3, 6). Тогда событие А-В появление чисел (2,4).

 

 

3. Определение вероятности события

 

Случайные события реализуются с различной возможностью. Одни происходят чаще, другие - реже. Для количественной оценки возможностей реализации события вводится понятие вероятности события.

Вероятность события - это число, характеризующее степень возможности появления события при многократном повторении испытаний.

Вероятность обозначается буквой Р (от англ. probability - вероятность). Вероятность является одним из основных понятий теории вероятностей. Существует несколько определений этого понятия.

Классическое определение вероятности заключается в следующем. Если известны все возможные исходы испытания и нет оснований считать, что одно случайное событие появлялось бы чаще других, т.е. события равновозможны и несовместны, то имеется возможность аналитического определения вероятности события.

Вероятностью Р(А)события Аназывается отношение числа благоприятствующих исходов т к общему числу равновозможных несовместных исходов п:

(1)

Свойства вероятности:

1. Вероятность случайного события А находится между 0 и 1.

.

2. Вероятность достоверного события равна 1.

.

3. Вероятность невозможного события равна 0.

.

 

Пример 1.

Найти вероятность выпадения числа, кратного 3, при одном бросании игрального кубика.

Решение:

Событие А- выпадение числа, кратного 3. Этому событию благоприятствуют два исхода: числа 3 и 6, т.е. т = 2. Общее число исходов состоит в выпадении чисел: 1 , 2, 3, 4, 5, 6, т.е. п = 6. Очевидно, что эти события равновозможны и образуют полную группу. Тогда искомая вероятность, по определению, равна отношению числа благоприятствующих исходов к числу всех исходов.

.

 

Пример 2.

В урне 10 белых, 5 красных и 5 зеленых шаров. Найти вероятность того, что вынутый наугад шар будет цветным (не белым).

Решение:

Число исходов, благоприятствующих событию А, равно сумме красных и зеленых шаров: т = 10. Общее число равновозможных несовместных исходов равно общему числу шаров в урне: п = 20. Тогда:

.

 

При определении вероятности события, по ее классическому определению, требуется выполнение определенных условий. Эти условия заключаются в равновозможности и несовместности событий, входящих в полную группу событий, вероятность которых надо определить. На практике не всегда можно определить все возможные варианты исходов, а тем более обосновать их равновозможность. Поэтому при невозможности удовлетворения требованиям классического определения вероятности используют статистическую оценку вероятности события. При этом вводится понятие относительной частоты появления события А, равной отношению , где т — число испытаний, в которых произошло событие А; п - общее число испытаний.

Я. Бернулли доказал, что при неограниченном увеличении числа испытаний относительная частота события А будет сколь угодно мало отличать от вероятности события А: .

Это равенство справедливо при неизменности условий, при которых проводится эксперимент.

Справедливость теоремы Бернулли была доказана и в многочисленных опытах по сравнению вероятностей, вычисленных классическим и статистическим методами. Так, в опытах Пирсона, по определению вероятности выпадения «герба» при выполнении 12 000 бросков, статистическая вероятность была равна 0,5016, а при 24 000 бросков — 0,5005, что показывает приближение к значению вероятности 0,5 по мере увеличения числа опытов. Близость значений вероятности, определенных различными способами, указывают на объективность возможности наступления этого события.

 

 

4. Теорема сложения вероятностей

 

Зная вероятности одних событий, можно вычислить вероятности других, если они связаны между собой. Теорема сложения вероятностей позволяет определить вероятность появления одного из нескольких случайных событий.

Теорема. Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий:

Р(А+В) = Р(А) + Р(В). (2)

Доказательство. Пусть п - общее число равновозможных несовместных элементарных исходов; m₁ - число исходов благоприятствующих событию А; т₂ - число исходов, благоприятствующих событию В. Так как А и В несовместные события, то событию А+В будет благоприятствовать m₁+m₂ исходов. Тогда, согласно классическому определению вероятности:

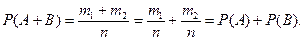
Расширяя это доказательство на п событий, можно доказать следующую теорему.

 

Теорема. Вероятность суммы конечного числа попарно несовместных событий А₁, А₂,..., А_п равна сумме вероятностей этих событий, т.е.

Р(А₁ + А₂ +…+А_п) = Р(А₁) + Р(А₂) +…+Р(А_п) (3)

Из этой теоремы можно вывести два следствия:

Следствие 1. Если события А₁ ,А₂,..., А_п образуют полную группу, то сумма их вероятностей равна единице, т.е. = Р(А₁) + Р(А₂) +…+Р(А_п) = 1. (4)

 

Следствие 2. Сумма вероятностей противоположных событий равна единице, т.е.

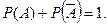
Доказательство. Противоположные события несовместны и образуют полную группу, а сумма вероятностей таких событий равна 1.

Пример 3.

Найти вероятность выпадения цифры 2 или 3 при бросании игральной кости.

Решение:

Событие А - выпадение цифры 2, вероятность этого события Р(А) = 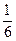. Событие В - выпадение цифры 3, вероятность этого события Р(В) = 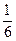. События несовместные, поэтому

Пример 4.

Получена партия одежды в количестве 40 штук. Из них 20 комплектов мужской одежды, 6 - женской и 14 - детской. Найти вероятность того, что взятая наугад одежда окажется не женской.

Решение:

Событие А - одежда мужская, вероятность

Событие В – одежда женская,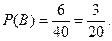

Событие С – одежда детская,

Тогда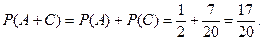

 

В том случае, если события А и В являются совместными, то справедлива следующая теорема.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, т. е.

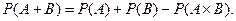( 5)

Доказательство. Пусть для полной группы событии, имеющих п исходов, т₁ исходов благоприятствуют событию А ,т₂ - событию В, а l исходов благоприятствуют как событию А , так и событию В, тогда

; ; .

Так как событие А + В состоит в том, что произошло событие А, либо событие В, либо событие А и В. Поэтому ему будет благоприятствовать m_l+m₂-l исходов. Следовательно,

Пример 5.

Вероятность попадания в мишень одного стрелка равна 0,65, а второго - 0,6. Определить вероятность поражения мишени при одновременных выстрелах двух стрелков.

Решение:

Так как при стрельбе возможно попадание в мишень двумя стрелками, то эти события совместные. Следовательно, Р(А + В) = Р(А) + Р(В) - Р(А×В) = 0,65 + 0,6 - 0,39 = 0,86.

5. Теорема умножения вероятностей

 

Событие А называется независимым от события В, если вероятность осуществления события А не зависит от того, произошло событие В или нет.

Например, при повторении бросания игральной кости вероятность выпадения цифры 1 (событие А) не зависит от появления или не появления цифры 1 при первом бросании кости (событие В).

Событие А называется зависимым от события В, если его вероятность меняется в зависимости от того, произошло событие В или нет.

Например,если в урне находятся черные и белые шары, то вероятность повторного появления черного шара (событие А) будет зависеть от того, какой шар вынули первый раз.

В случае зависимых событий А и В вводится понятие условной вероятности, под которой понимается вероятность события А при условии, что событие В произошло. Обозначается Р(А/В).

Пример 6.

В урне находится 10 шаров: 3 белых и 7 черных. Первым был вынут черный шар, найти вероятность того, что второй шар будет черным.

Решение:

Вероятность появления черного шара первый раз (событие В) равно Р(В) = 7/10; а вероятность появления его второй раз (событие А), при условии, что событие В произошло, равно Р(А/В) = 6/9, так как в урне осталось 9 шаров, из них 6 черных.

 

Рассмотрим закон умножения вероятностей для независимых событий.

Произведением двух событий А и В называют событие С = А×В, состоящее в совместном осуществлении этих событий.

Теорема. Вероятность произведения 2 независимых событий А и В равна произведению вероятностей этих событий:

Этот закон справедлив и для п независимых событий.

(6)

Пример 7.

В билете 3 раздела. Из 40 вопросов первого раздела студент знает 30 вопросов, из 30 вопросов второго - 15, из 30 вопросов третьего - 10. Определить вероятность правильного ответа студента по билету.

Решение:

Учитывая, что ответ на каждые разделы есть независимые события A₁,A₂ и А₃, а их вероятности соответственно равны:

Тогда вероятность правильного ответа на билет Р(В), можно найти по формуле (6).

Теорема. Вероятность произведения двух зависимых событий А и В равна произведению одного из них на условную вероятность второго, вычисленную при условии, что первое событие осуществилось.

P(AиB) = P(A×B) = P(A) • Р(В/А). (7)

Формула умножения вероятностей может быть обобщена на случай п событий A₁, A₂,..., A_n:

Причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие произошли.

 

Пример 8.

В группе из 20 человек 5 студентов не подготовили задание. Какова вероятность того, что два первых студента, вызванные наугад, будут не готовы к ответу.

Решение:

Вероятность того, что первый студент не готов к ответу Р(А) = 5/20, вероятность того, что и второй студент также не подготовлен, как и первый, Р(В/А) = 4/19, тогда для ответа на вопрос воспользуемся формулой:

P(AиB) = P(A×B) = P(A) • Р(В/А) =

 

События A₁, A₂,..., A_n называются независимыми в совокупности, если каждое из этих событий и событие, равное произведению любого числа остальных событий, независимы.

Теорема, Вероятность появления хотя бы одного из событий A₁, A₂,..., A_n независимых в совокупности, равна разности между единицей и произведением вероятностей проти­воположных событий т.е.

Р(А₁+А₂+...+А_п)= . (8)

Пример 9.

В трех театральных кассах продаются билеты. Вероятность наличия билетов за час до начала спектакля в первом театре равна 0,7, в кассе второго - 0,3, а в кассе третьего - 0,5. Какова вероятность того, что за час до начала спектакля имеется возможность купить билет хотя бы в одной кассе.

Решение:

Событие А - возможность купить билеты хотя бы в одной кассе. Тогда противоположное событие обозначим . Оно наступит тогда, когда наступит событие . Тогда

Пример 10.

Вероятность попадания в цель при стрельбе из трех орудий такова: Р₁ = 0,75; Р₂ = 0,8; Р₃ = 0,85. Какова вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий?

Решение:

Пример 11.

Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго - 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один стрелок.

Решение:

Вероятность того, что в мишень попадает первый стрелок и не попадает второй, равна:

Вероятность того, что попадет второй стрелок в мишень и не попадет первый, равна:

Вероятность того, что в мишень попадет только один стрелок, равна сумме этих вероятностей:

6. Формула полной вероятности. Формула Байеса

 

Следствием основных законов сложения и умножения вероятностей является формула полной вероятности.

Пусть требуется найти вероятность некоторого события В, которое может произойти вместе с одним из событий A₁, A₂,..., A_п, образующих полную группу несовместных событий. Так как события A₁, A₂,..., A_п образуют полную группу, то событие В может произойти только в комбинации с каким-либо из них:

В = А₁В + А₂В + ... +А_пВ.

Так как событие A₁, A₂,..., A_п несовместны, то и комбинации А₁В, А₂В, А_пВ несовместны.

Согласно закону сложения несовместных событий имеем:

Каждое из слагаемых является вероятностью произведения двух зависимых событий.

(9)

Теорема. Вероятность события В, которое может наступить только при условии появления одного из событий A₁, A₂,..., A_п, образующих полную группу попарно несовместных событий, равна сумме произведений вероятностей каждого из событий A₁, A₂,..., A_п на соответствующую условную вероятность события В.

Полученная формула называется формулой полной вероятности, а события A₁, A₂,..., A_п - гипотезами.

 

Пример 12.

На склад ежедневно поступают детали с трех предприятий. С первого - 30 деталей, со второго - 20 и с третьего - 40. Установлено, что 2, 4 и 5% продукции этих предприятий, соответственно, имеют дефекты. Найти вероятность того, что взятая наугад деталь будет дефектна.

Решение:

Обозначим: В - взятая наугад деталь дефектна; А₁ - деталь изготовлена на первом предприятии, А₂ - деталь изготовлена на втором предприятии, A₃ - деталь изготовлена на третьем предприятии. События A₁, A₂,и A₃ образуют полную группу несовместных событий и

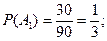
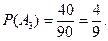
Условные вероятности события В равны:

Р(В/А₁) = 0,02; Р(В/А₂) = 0,04; Р(В/А₃) = 0,05.

Тогда

С формулой полной вероятности тесно связана формула Байеса, названная по имени английского математика Томаса Байеса (1702-1761). Формула Байеса позволяет переоценить вероятности гипотез после того, как в результате опыта произошло событие В.

Пусть имеется полная группа несовместных событий A₁, A₂,..., A_п. Вероятности этих событий до опыта (априорные) известны и равны соответственно Р(А₁), Р(А₂), … Р(А_п). В результате проведения опыта произошло событие В. Необходимо найти апостериорные (после опыта) вероятности событий A_j , т.е. следует определить условную вероятность Р(A_j / В)

Согласно закону умножения вероятностей имеем:

Тогда,

Отсюда,

Выражая Р(В) с помощью формулы полной вероятности, имеем:

(10)

 

Пример 13.

Имеются три урны: в первой из них 5 белых шаров и 4 черных; во второй - 3 белых и 6 черных; в третьей - 2 белых и 7 черных. Из выбранной наугад урны вынимают шар. Он оказался черным. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.

Решение:

Гипотезы: А₁ - выбор первой урны; А₂ - выбор второй урны; А₃ - выбор третьей урны. До опыта все гипотезы равновероятны:

Событие В - появление черного шара. Условные вероятности этого события равны:

Тогда по формуле Байеса имеем:

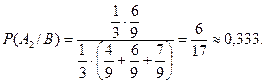
Таким образом, наиболее вероятным был выбор третьей урны.

 

 

КОНТРОЛЬНАЯ РАБОТА

Классическое определение вероятности

1. Из букв слова «вероятность» наугад выбирается одна буква. Какова вероятность того, что выбранная буква будет: А - согласной; В - гласной; С - буква «о»?

 

2. Набирая номер телефона, абонент забыл одну цифру и набрал ее наугад. Какова вероятность того, что набранная цифра правильная?

 

3. На странице книги имеется 2 500 букв. Буква «а» встречается 190 раз. Какова вероятность того, что случайно выбранная буква не есть буква «а»?

 

Теоремы сложения и умножения вероятностей

4. В магазин поступили телевизоры, 60% которых поставило первое предприятие, 25% - второе и 15% - третье. Какова вероятность того, что купленный телевизор изготовлен на первом или третьем предприятии?

 

5. В мастерской два мастера работают независимо друг от друга. Вероятность того, что в течение часа первый мотор не потребует внимание мастера, равна 0,9, для второго мотора эта вероятность равна 0,89. Найти вероятность того, что в течение часа ни один из моторов не потребует внимание мастера.

 

6. Предположим, что в некоторой семье имеется 2 ребенка. 1) Какова вероятность того, что оба ребенка - девочки? 2) Если известно, что, по крайней мере, один ребенок девочка, то какова вероятность того, что обе - девочки? 3) Если известно, что старший ребенок - девочка, то какова вероятность, что оба ребенка девочки?