 |
|
Свойства числовых рядов.
РЯДЫ
Числовой ряд:  , члены ряда:
, члены ряда: 
| числа |
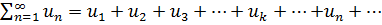

|

|
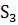
|

|

|

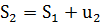
 …
…


|
Частичные суммы числового ряда образуют последовательность:
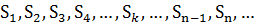
Ряд сходится, если существует конечный предел:  ; в противном случае – ряд расходится.
; в противном случае – ряд расходится.
| Классификация числовых рядов | |
| Знакоположительные | 
|
| Знакопеременные | 
|
| Знакочередующиеся | 
|
Необходимый признак сходимостиряда:
- если ряд 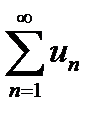 сходится, то
сходится, то 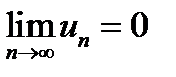 .
.
- если  , то ряд расходится.
, то ряд расходится.
Свойства числовых рядов.
1. Если сходится ряд 
| отбрасываются |
| n-остаток числового ряда |
то сходится и ряд  , полученный отбрасыванием (или приписыванием) первых n членов ряда:
, полученный отбрасыванием (или приписыванием) первых n членов ряда:  .
.
Чтобы ряд 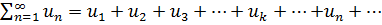 сходился необходимо и достаточно, чтобы
сходился необходимо и достаточно, чтобы  (из сходимости остатка следует сходимость исходного ряда).
(из сходимости остатка следует сходимость исходного ряда).
2. Если сходится ряд  , то сходится и ряд
, то сходится и ряд  ,
,
3. Если сходятся ряды


то сходится и ряд

Достаточные признаки сходимости ряда:
I признак сравнения: пусть даны два ряда 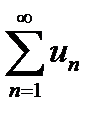 и
и 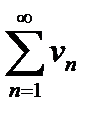 , причём
, причём  , тогда:
, тогда:
1) если ряд 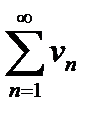 - сходится, то и ряд
- сходится, то и ряд 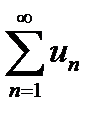 - сходится;
- сходится;
2) если ряд  - расходится, то и ряд
- расходится, то и ряд  - расходится.
- расходится.
| сходится расходится |
| Сходится расходится |

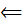


II признак сравнения: если существует конечный предел 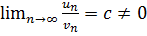 , то ряды
, то ряды 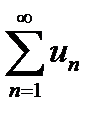 и
и 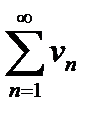 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
| Эталонные ряды (используемые для сравнения) | ||
| геометрическая прогрессия | 
| 
|

| ||
| обобщённый гармонический ряд | 
| 
|

| ||
| гармонический ряд | 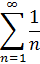
| расходится |
 eсли общий член ряда – рациональная дробь eсли общий член ряда – рациональная дробь 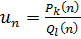 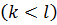 , то исследовать этот ряд на сходимость можно сравнением с рядом , то исследовать этот ряд на сходимость можно сравнением с рядом 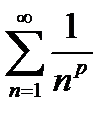 , где , где 
|
| Достаточные признаки сходимости для числовых рядов с положительными членами | |||
| Название признака | Признак Даламбера: | Радикальный признак Коши: | |
| Вывод о сходимости числового ряда | Если для ряда 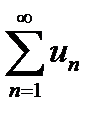 , существует , существует 
| Если для ряда 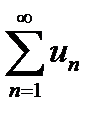 , существует , существует 
| |
| Ряд сходится | 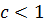
| ||
| Невозможно сделать вывод о сходимости ряда | 
| ||
| Ряд расходится | 
| ||
| Эффективное применение | общий член ряда содержит множитель  или или 
| общий член ряда содержит выражение в степени  или или 
| |
Интегральный признак Коши: пусть дан ряд 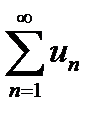 , где , где  . Тогда если . Тогда если  при при  непрерывная положительная и монотонно убывающая функции и непрерывная положительная и монотонно убывающая функции и  , то ряд сходится, если , то ряд сходится, если  , то расходится. , то расходится.
| |||
Знакопеременные ряды  сходится, если сходится ряд
сходится, если сходится ряд  , составленный из абсолютных величин его членов. Знакопеременный ряд в этом случае называют абсолютно сходящимся. Если же знакопеременный ряд сходится, а ряд
, составленный из абсолютных величин его членов. Знакопеременный ряд в этом случае называют абсолютно сходящимся. Если же знакопеременный ряд сходится, а ряд  расходится, то его называют условно сходящимся.
расходится, то его называют условно сходящимся.
Достаточный признак сходимостидлязнакочередующихсярядов - признак Лейбница:
- признак Лейбница:
Если для знакочередующегося ряда  выполнены условия:
выполнены условия:

то ряд сходится, если одно из условий не выполняется, то ряд расходится.
Условие  выполнено, если:
выполнено, если:
1. 
2. 
3. пусть  такая, что
такая, что  :
: 
Функциональный ряд: 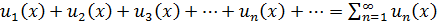
| функции |
Степенной ряд: 

Областью сходимости степенного ряда является круг с центром в точке  , радиус которого может быть определён применением либо признака Даламбера, либо признака Коши:
, радиус которого может быть определён применением либо признака Даламбера, либо признака Коши:
 или
или 
Для любого степенного ряда 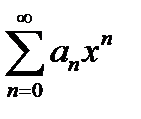 существует число
существует число 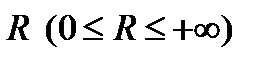 называемое радиусом сходимости ряда, которое обладает свойствами:
называемое радиусом сходимости ряда, которое обладает свойствами:
- при любом х, удовлетворяющему неравенству  , ряд сходится,
, ряд сходится,
- при любом х, удовлетворяющему неравенству  , ряд расходится.
, ряд расходится.
Промежуток 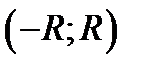 называется интервалом сходимости ряда.
называется интервалом сходимости ряда.
Вопрос о сходимости ряда на концах интервала, т.е. при  исследуется отдельно.
исследуется отдельно.
Для определения радиуса сходимости можно использовать формулы:
 или
или 
- если  , то ряд сходится в единственной точке
, то ряд сходится в единственной точке 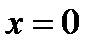
- если 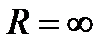 , то ряд сходится на всей числовой прямой
, то ряд сходится на всей числовой прямой