 |
|
Методы применения определенного интеграла
ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Замена переменной в определенном интеграле
Пусть для вычисления определенного интеграла
сделана подстановка x=φ(t).
Теорема 1.Если:
1) φ(t), φʹ(t) 
С[α;β] (t [α;β]);
2) D( φ)= [α;β], E(φ) = [a;b];
(D( φ) – область определения; E(φ) – область значений)
3) φ(α)=a, φ(β)=b,
то
. (1)
Док.▼ Пусть F(x) – есть первообразная для f(x) на [a;b]. Тогда
.
Поскольку
(F(φ(t)))ʹ = f(φ(t))·φʹ(t),
то F(φ(t)) является первообразной для f(φ(t))·φʹ(t), t [α;β].
По формуле Ньютона-Лейбница
.
▲
Выражение (1) называется формулой замены переменной в определенном интеграле.
Замечания.
1. При вычислении определенного интеграла методом замены переменной возвращаться к старой переменной не требуется.
2. Наряду с подстановкой x=φ(t) применяется также подстановка t=ψ(x).
Пример 1.Вычислить
Решение▼
.
▲
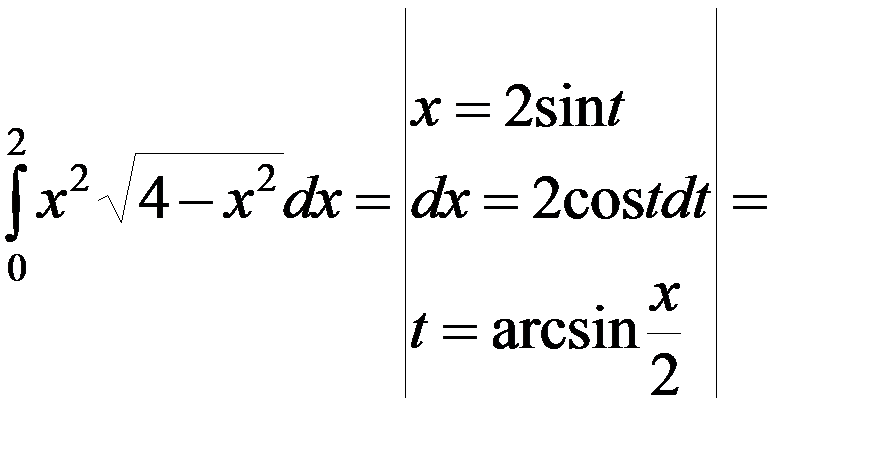
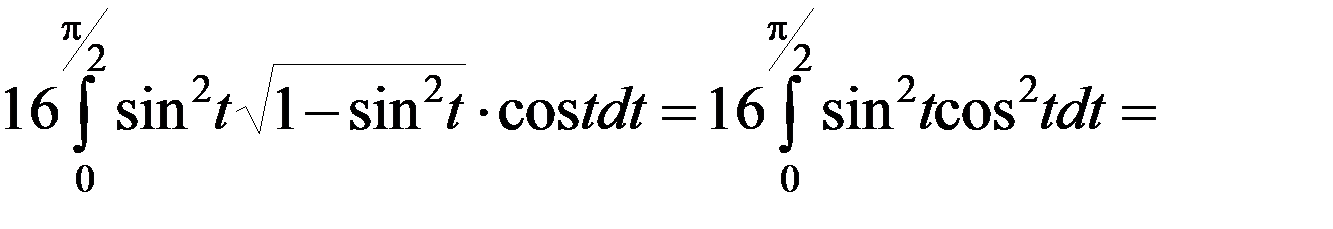
Интегрирование по частям
Теорема 2.Если u(x), v(x):uʹ(x), vʹ(x) С[a;b], то
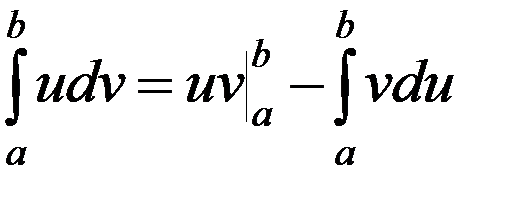. (2)
Док.▼ На отрезке [a;b] справедливо равенство
(uv)ʹ =uʹv + uvʹ.
Следовательно, функция uv есть первообразная для uʹv + uvʹ.
По формуле Ньютона-Лейбница
.
Следовательно
.
▲
Пример 1.Вычислить
Решение▼
.
▲
5.3. Интегрирование четных и нечетных функций в симметричных пределах
Пусть f(x) С[–a; a] ([–a; a] – отрезок, симметричный относительно точки x =0).
Тогда
Например,
, 
.
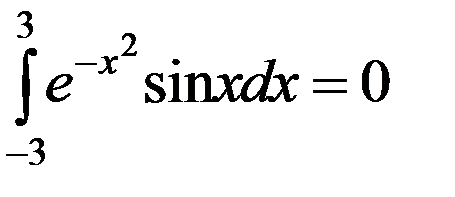ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Методы применения определенного интеграла
Пусть требуется найти значение какой-либо геометрической или физической величины А(площадь фигуры, объем тела, давления жидкости на вертикальную пластину и.т.д.).
А = А(х), х 
[a; b].
Предполагается, что величина А аддитивна:
,
где Аi=А(х), х [хi–1; хi];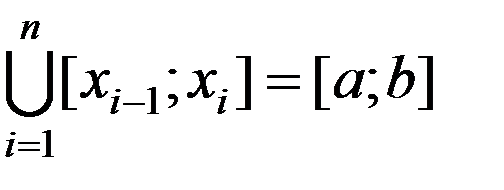 
.
Для нахождения величины А применяются два метода – метод интегральных сумм и метод дифференциалов.
1. Метод интегральных сумм.
а). Отрезок [a; b] разбивается на n частей [хi–1; хi],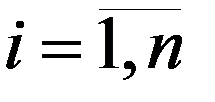 
:
.
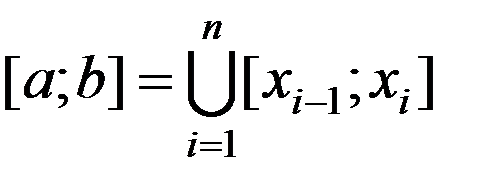При этом величина А разобьется на n элементарных слагаемых ∆Аi, 
:
А = ∆А1+ ∆А2+…+∆Аn.
б). Каждое элементарное слагаемое представляется в виде произведения некоторой функции(определяется из условия задачи), вычисленной в произвольной точке отрезка [хi–1; хi] на его длину:
∆Аi≈ f(ci)∆xi.
Приближенное значение величины А есть интегральная сумма:
.
Точное значение величиныА:
.
Таким образом, метод интегральных сумм основан на представлении интеграла как суммы бесконечно большого числа бесконечно малых слагаемых.
Данный метод применен для выяснения геометрического и физического смысла определенного интеграла.
2. Метод дифференциалов.
а). На отрезке [a; b] выбирается произвольное значение х и рассматривается переменный отрезок [a; х]. В данном случае
А = А(х), х 
[a; b]. (1)
б). Находится главная часть приращения ∆А при ∆х =dx, т.е. дифференциал dА функции (1):
dА= f(x)dx, (2)
где f(x) – функция, определяемая условием задачи.
в). Величина А находится путем интегрирования выражения (2):
.
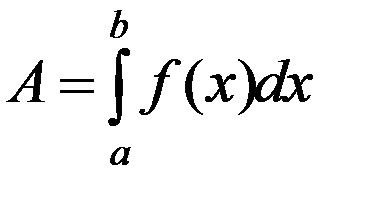Таким образом, основная идея метода дифференциалов состоит в составлении дифференциала искомой величиныАи нахождении ее значения путем интегрирования данного дифференциала.