 |
|
Двойственность в задачах линейного программирования. Двойственная задача линейного программирования.
Каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной, или прямой. Их связь - решение одной из них может быть получено непосредственно из решения другой.
Переменные двойственной задачи Yt 
называются объективно обусловленными оценками, или двойственными оценками, или «ценами» ресурсов, или теневыми ценами.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
1) целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид (<=), в задаче на минимум — вид (>=);
2) матрица А, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица AT двойственной задаче получаются друг из друга транспонированием;
3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи — числу переменных в исходной;
4) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной;
5) каждому ограничению одной задачи соответствует переменная другой задачи, номер переменной совпадает с номером ограничения. При этом ограничению, записанному в виде неравенства <=, соответствует переменная, связанная условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Модель исходной (прямой) задачи в общем виде может быть записана следующим образом: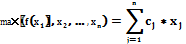 
Xj >=0 j=1,2,…n,
а модель двойственной задачи
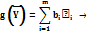min,
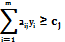
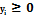
Две приведенные задачи образуют пару симметричных двойственных задач. Основные утверждения о взаимно двойственных задачах содержатся в двух следующих теоремаx.
Первая теорема двойственности
Для взаимно двойственных задач имеет место один из взаимоисключающих случаев.
1.В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают
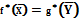
2.В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.
3.В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым.
4.Обе из рассматриваемых задач имеют пустые допустимые множества.
Вторая теорема двойственности (теорема о дополняющей нежесткости)
Пусть -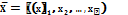 
допустимое решение прямой задачи, a 
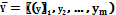-допустимое решение двойственной задачи. Для того чтобы они были оптимальными решениями соответственно прямой и двойственной задач, необходимо и достаточно, чтобы выполнялись следующие соотношения: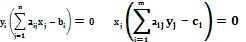 
Данные условия позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.
Теорема об оценках
Значения переменных yi в оптималъном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений (неравенств) прямой задачи на величину 