Главная | Обратная связь

Интегрирование простейших рациональных дробей

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ

Общие сведения о комплексных числах

• Комплексным числом называется выражение

z = x + iy,

где x 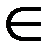R, y 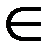R(x– вещественная часть, y– мнимая часть),i – мнимая единица, i² = –1.

Множество комплексных чисел

С={x + iy}.

• Если x =0, то число

z = iy

называется мнимым числом, если y=0, то число

z =x

отождествляется с вещественным числом. Следовательно

R С.

• Два комплексных числа

z₁ = x₁ + iy₁, z₂ = x₂ + iy₂

называются равными, если x₁ = x₂, y₁ = y₂.

Комплексное число равно нулю, если x = 0, y= 0. Понятие «больше» или «меньше» для комплексных чисел не вводится.

• Два комплексных числа

z = x – iy, z = x + iy

называются сопряженными.

Общие сведения о рациональных функциях

• Функциявида

P_n(x)=a₀xⁿ + a₁x^n–1+ a₂x^n–2+…+ a_n–1x + a_n, (1)

гдеn N, a_j =const, ,

называется алгебраическим полиномомn-й степени или целой рациональной функцией.

Корнем выражения (1) называется такое значение x₀ С, при котором P_n(x)=0.

Теорема 1. Если x₀ корень полинома (1), то полином делится без остатка на x –x₀, т.е.

P_n(x)= (x –x₀)P_n–1(x), (2)

где P_n–1(x) – полином степени (n–1).

^{_______________________________}

Теорема 2. (Основная теорема алгебры). Всякий полином n-й степени имеет хотя бы один корень, вещественный или комплексный.

^{_______________________________}

Теорема 3. Всякий полином n-й степени может быть представлен в виде

P_n(x)=a₀(x –x₁)(x –x₂)·…·(x –x_n), (3)

где x₁,x₂,… ,x_n– корни полинома;a₀ – коэффициент при xⁿ.

^{_______________________________}

Множители(x –x_i)называются линейными множителями.

Например

x³ –x² +4x – 4= (x – 1)(x – 2i)(x + 2i).

Проверкадля x = 2i:

(2i)³ – (2i)² +4·2i – 4 = 8i²i – 4i² + 8i – 4 =

= –8i + 4+ 8i – 4 = 0.

Если в разложении (3) какой-либо корень встретился k раз, то он называется корнем кратности k. Если корень встретился один раз (k = 1), он называется простым.

Разложение (3) можно представить в виде:

, (4)

где r – число различных корней; k₁ +k₂+…+k_r= n.

Теорема 4. Если два полинома тождественно равны друг другу, то коэффициенты одного полинома равны соответствующим коэффициентам другого.

^{_______________________________}

Например, если

ax³ + bx² +cx + d ≡ x³ – 3x² + 1,

то a=1, b= –3,c= 0, d=1.

Теорема 5. Если полином P_n(x) с вещественными коэффициентами имеет комплексный корень a+ ib, то он имеет и сопряженный корень a– ib.

^{_______________________________}

В разложение (3) комплексные корни входят сопряженными парами.

Перемножим линейные множители

(x–(a + ib))·(x –(a – ib))=(x – a)– ib))·(x – a)+ ib)) =

= (x – a)²– i²b² = (x – a)² + b² = x² –2ax +a²+ b² =

x²–px +q,

где p = –2a; q = a²+ b².

Таким образом, произведение линейных множителей с сопряженными корнями можно заменить квадратичным полиномом с вещественными коэффициентами.

С учетом вышеизложенного справедлива следующая теорема.

Теорема 6. Всякий полином с вещественными коэффициентами разлагается на линейные и квадратичные множители с вещественными коэффициентами, т.е.

,(5)

при этом k₁ + k₂+…+k_r+2(s₁ + s₂+…+s_m) = n.

^{_______________________________}

Примеры 1разложений (5):

1) x⁴ – 1 = (x– 1)(x+ 1)(x² + 1);

2) x³ – 16x = x(x² – 16) =x(x– 4)(x+ 4).

• Функция вида

называется дробно-рациональной, если P_m(x) и Q_n(x) полиномы степени m и n соответственно.

Рациональная дробь называется правильной, если m<n, в противном случае (m≥ n) - неправильной.

Всякую неправильную рациональную дробь можно путем деления числителя на знаменатель представить в виде суммы полинома и правильной рациональной дроби:

.

Например

- неправильная рациональная дробь.

Разделим числитель на знаменатель

Получили частное

L(x)=2x – 3

и остаток

R(x) = –1.

Следовательно

.

•Правильные дроби

( ) ,

( ) , k N\{1},

( ) ,p² – 4q<0,

( ) , k N\{1}, p² – 4q<0,

где A, a, M, N, p, q R, называются простейшими рациональными дробям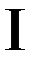и , , и типов.

Теорема 7. Всякую правильную рациональную дробь , знаменатель которой разложен на множители

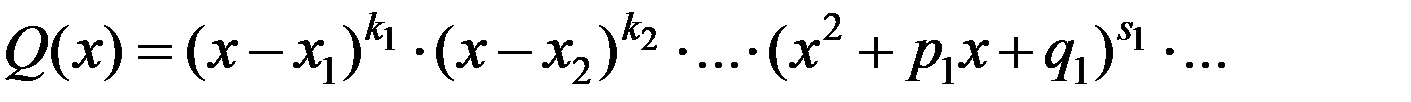
можно представить единственным образом в виде следующей суммы простейших дробей:

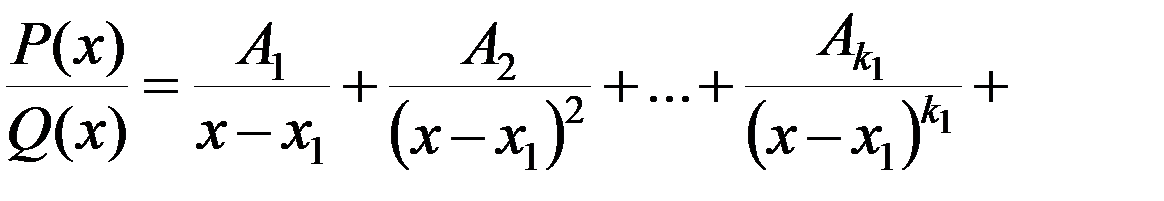
(6)

,

где A₁, A₂,…,B₁, B₂,…,C₁, D₁,…,M₁,…,N₁,… R.

^{_______________________________}

Примеры 2:

1. ;

2. ;

3.

.

Для нахождения неопределенных коэффициентов A₁, A₂,…,B₁, B₂,…,C₁, D₁,…,M₁,…,N₁,… в выражении (6) применяется метод сравнивания коэффициентов.

Существо метода:

1. Правая часть (6) приводится к общему знаменателю Q(x), в результате получается тождество

,

где S(x) – полином с неопределенными коэффициентами.

2. Так как в полученном тождестве знаменатели равны, то тождественно равны и числители, т.е.

P(x)=S(x). (7)

3. Приравнивая коэффициенты при одинаковых степенях х (по теореме 4 о тождестве полиномов) в обеих частях тождества (7), получим систему линейных уравнений, из которой определяются коэффициенты A₁, A₂,…,B₁,…

Пример 3.Представить дробь

в виде суммы простейших дробей.

Решение_▼ Согласно теореме 7

.

Следовательно

;

.

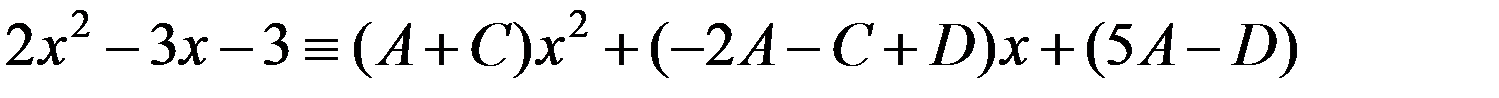Приравниваем коэффициенты при x², x¹, x⁰:

Решая систему, находим A = –1; C = 3; D = –2.

Таким образом

.

^▲

Интегрирование простейших рациональных дробей

1. .

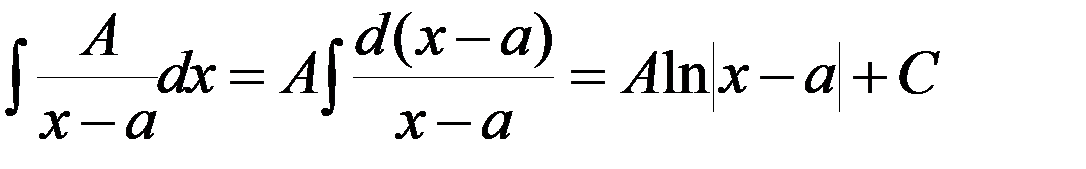2.

.

3. , p² – 4q<0.

В знаменателе выделяется полный квадрат и применяется метод замены переменной:

.

.

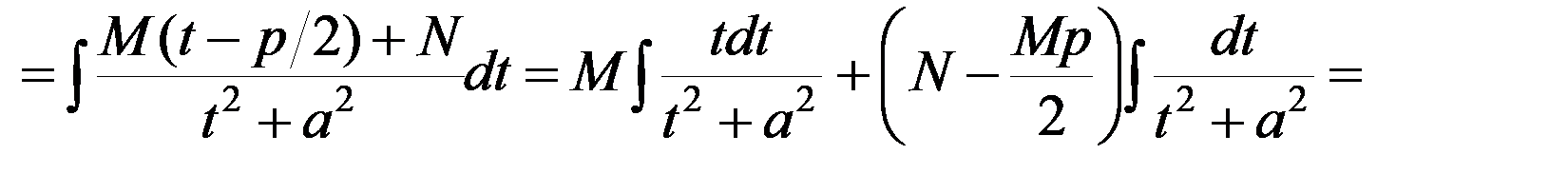
4. , k N\{1}, p² – 4q<0,

.

Первый интеграл

.

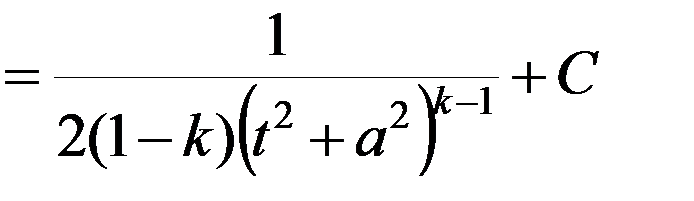Второй интеграл

,(8)

где .

Рассматриваем интеграл

.

Найденный интеграл подставляем в выражение (8):

,

т.е.

.

Полученная формула дает возможность найти интеграл J_k для любого натурального числа k>1.

Пример 4.Найти интеграл

.

Решение_▼ В данном случае a=1, k =3.

;

;

.

^▲