 |
|
Универсальная тригонометрическая подстановка
Интегрирование рациональных дробей
Общее правило интегрирования рациональных дробей.
1. Если дробь неправильная, то представить ее в виде суммы полинома и правильной дроби.
2. Разложить знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
3. Проинтегрировать полином и полученную сумму простейших рациональных дробей.
Пример 5.Найти интеграл
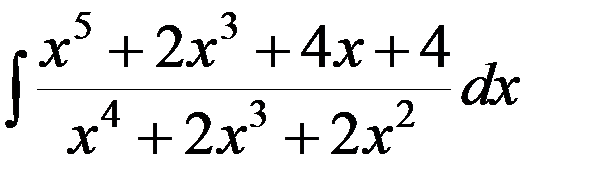 .
.
Решение▼ Неправильную дробь представляем в виде суммы полинома и правильной дроби:
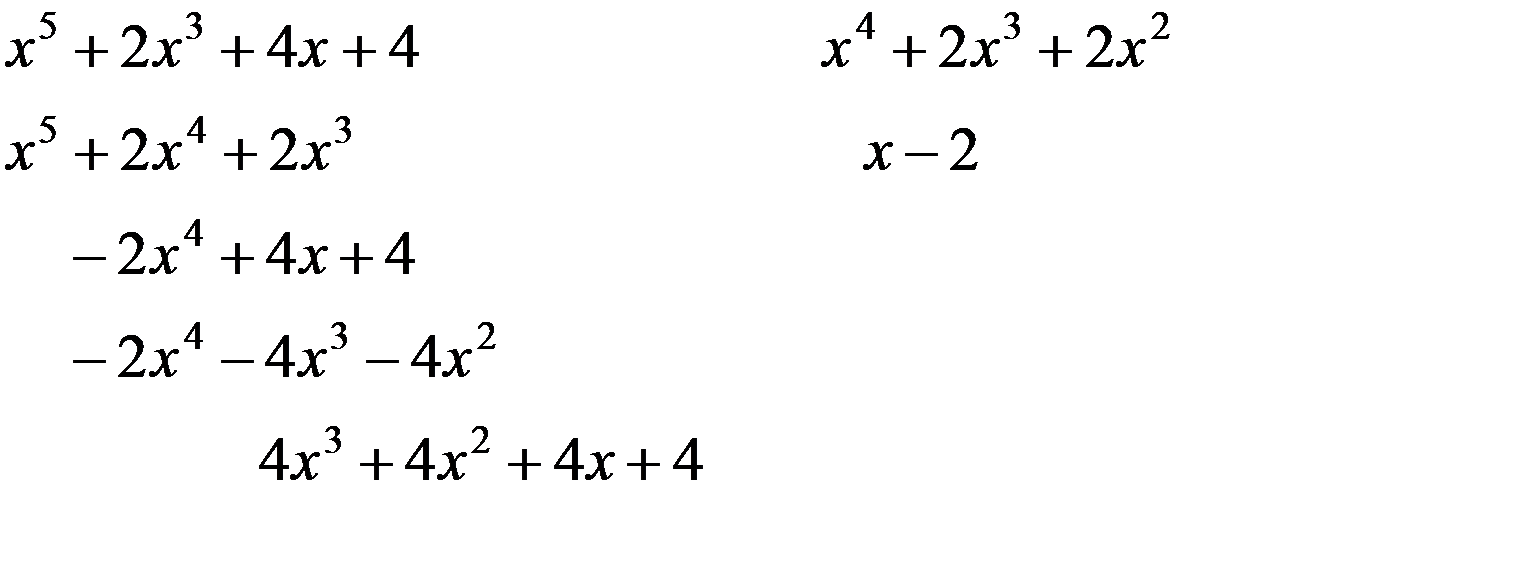
Получаем
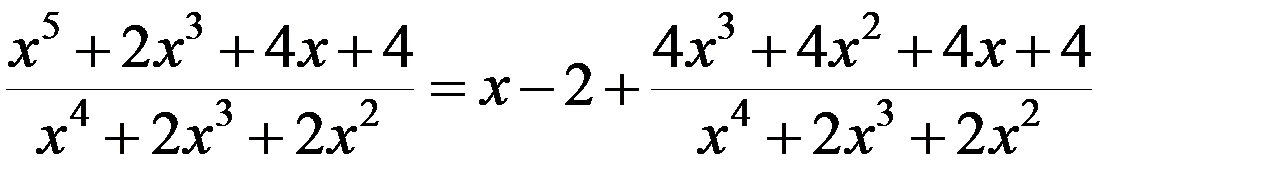 .
.
Разложим правильную рациональную дробь на простейшие дроби:
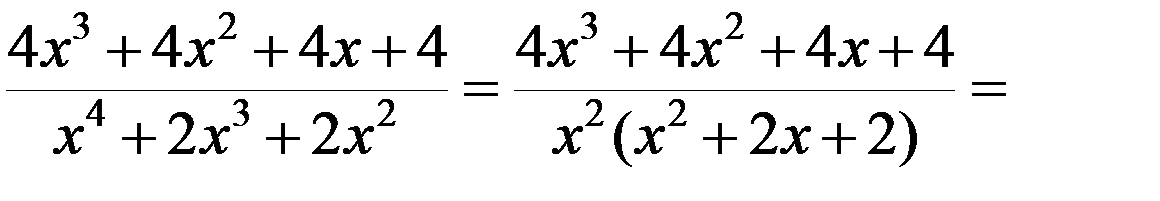
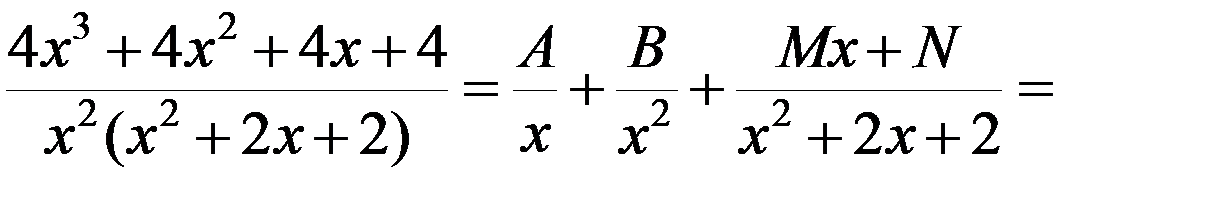
 .
.
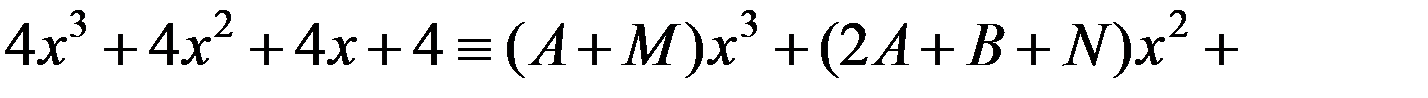
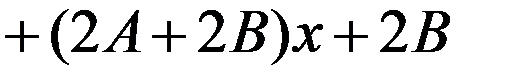 .
.
Получаем систему линейных уравнений:
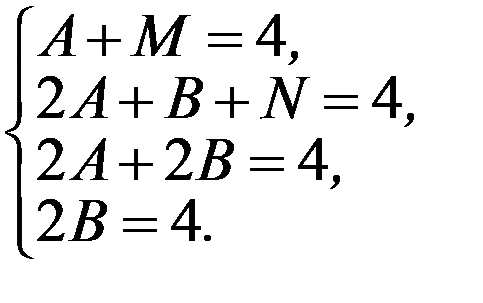
Находим: B = 2, A = 0, M = 4, N = 2.
Таким образом
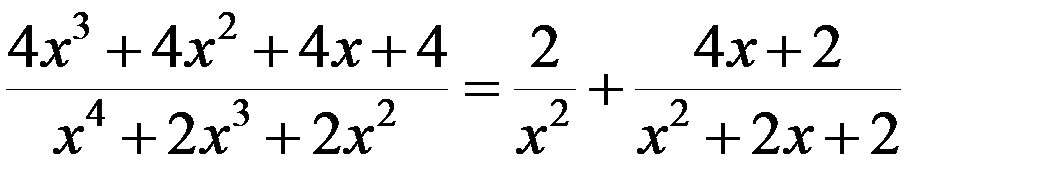
и
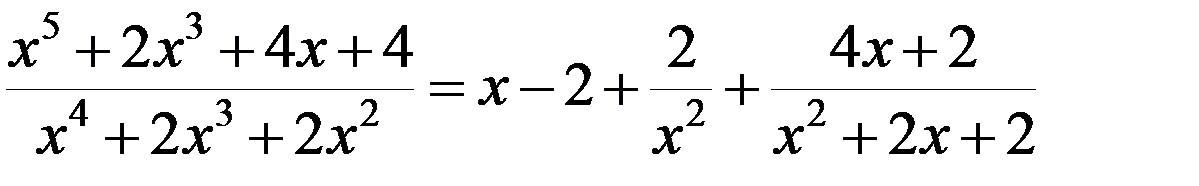 .
.
Производим интегрирование

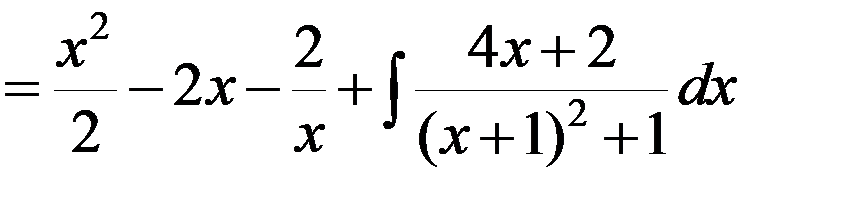 .
.
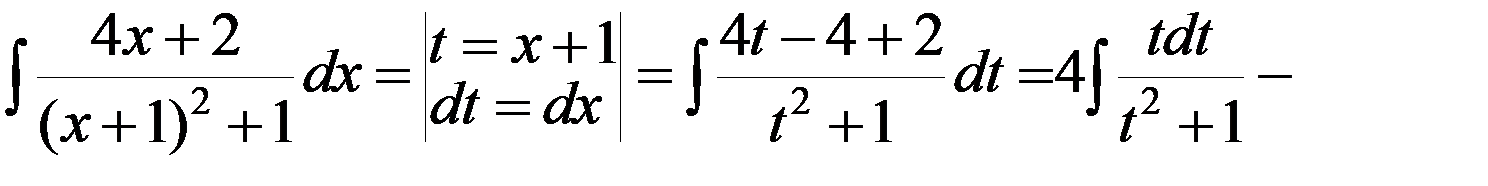

 .
.
Следовательно

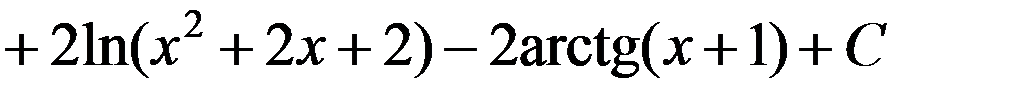 .
.
▲
Любая рациональная функция интегрируется в элементарных функциях.
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Универсальная тригонометрическая подстановка
Обозначим через
R(sinx; cosx)
функцию с переменными sinx и cosx, над которыми выполняются рациональные действия (сложение, вычитание, умножение, деление).
Нахождение неопределенных интегралов типа

осуществляется подстановкой
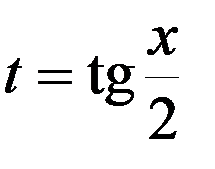 ,
,
которая называется универсальной.
Действительно
 ;
;
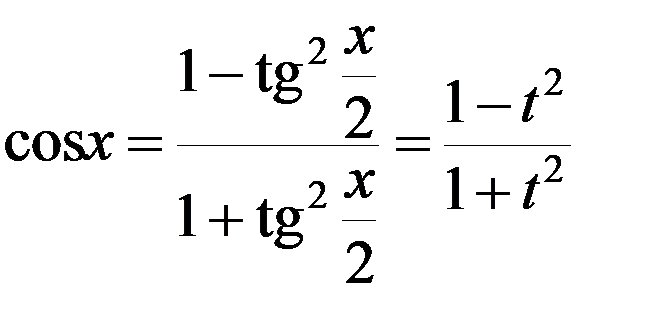 ;
;
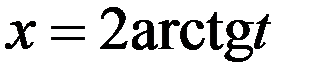 ;
; 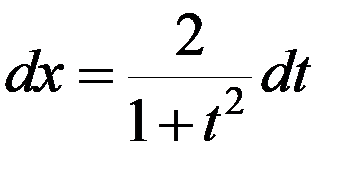 .
.
Поэтому
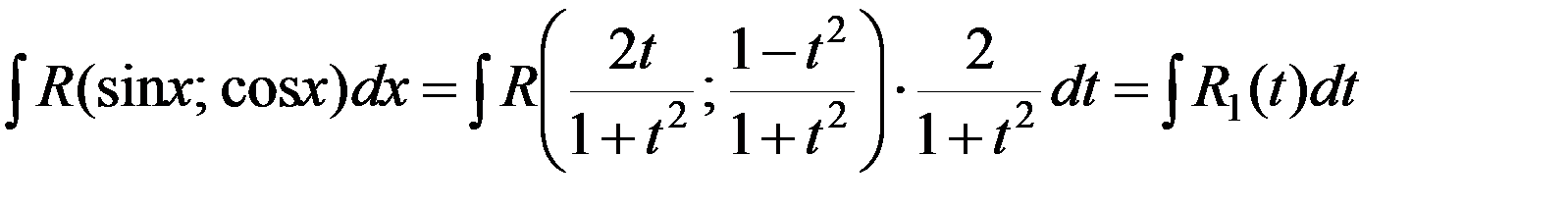 ,
,
где R1(t) – рациональная функция от t.
Другие подстановки:
1. Если функция R(sinx; cosx) – нечетная относительно sinx, т.е.
R(–sinx; cosx) = –R(sinx; cosx),
то используется подстановка
t = cosx.
2. Если функция R(sinx; cosx) – нечетная относительно cosx, т.е.
R(sinx; –cosx) = –R(sinx; cosx),
то используется подстановка
t = sinx.
3. Если функция R(sinx; cosx) – четная относительно sinx и cosx, т.е.
R(–sinx; –cosx) = R(sinx; cosx),
то используется
t = tgx.
Такая же подстановка применяется, если интеграл имеет вид
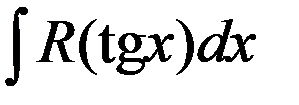 .
.
Пример 1.Найти интеграл
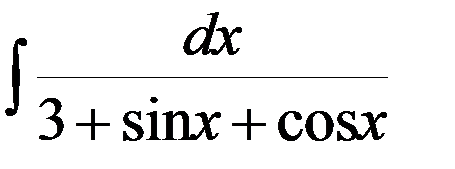 .
.
Решение▼
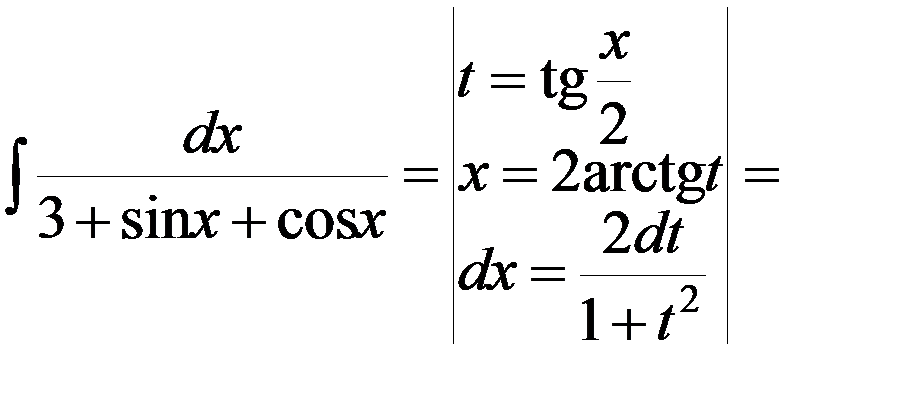
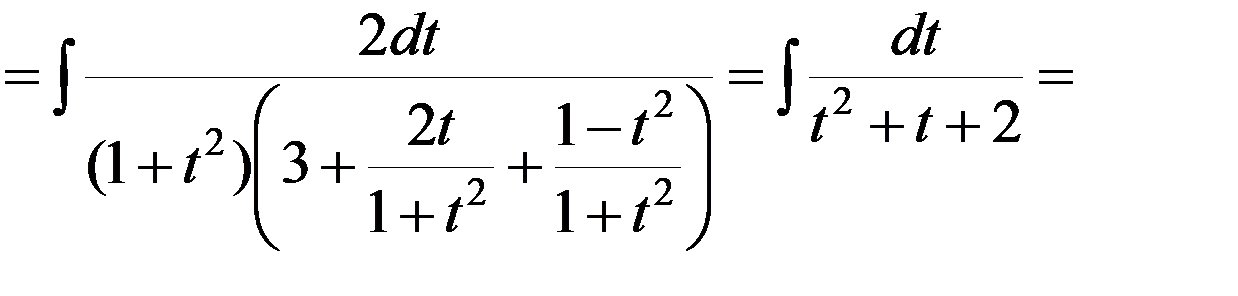

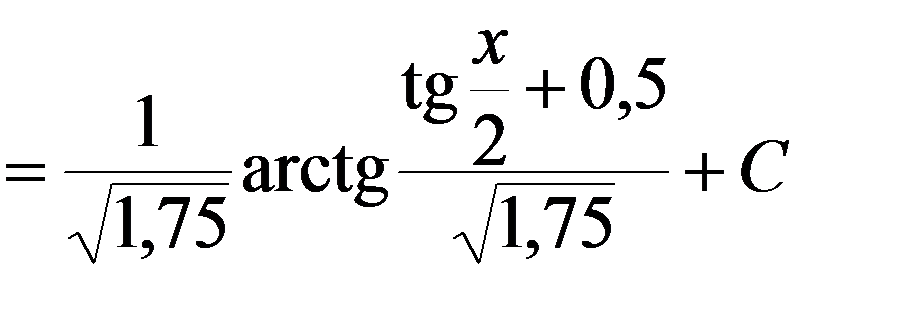 .
.
▲
Пример 2.Найти интеграл
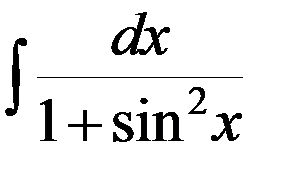 .
.
Решение▼
Подынтегральная функция – четная относительно sinx и cosx, так как
R(–sinx;–cosx)=  =R(sinx; cosx).
=R(sinx; cosx).
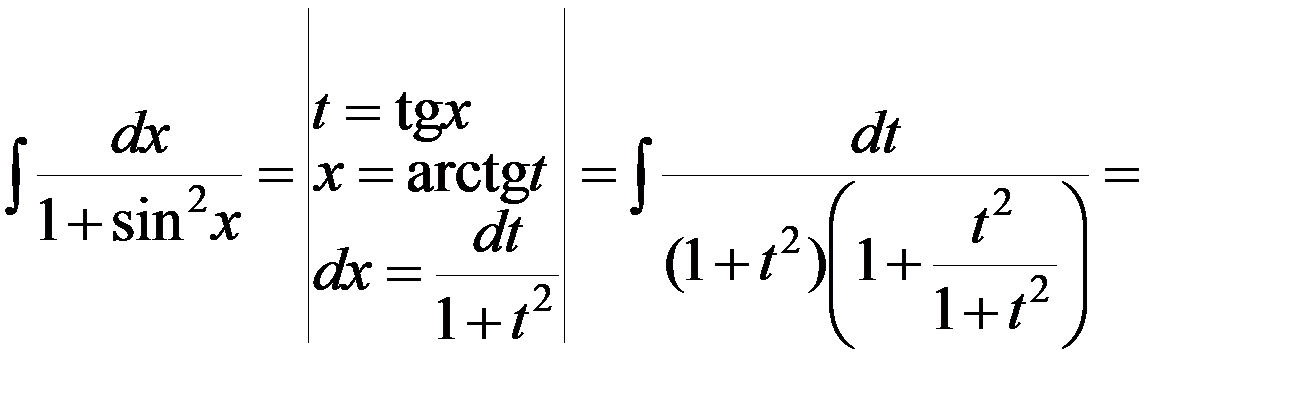
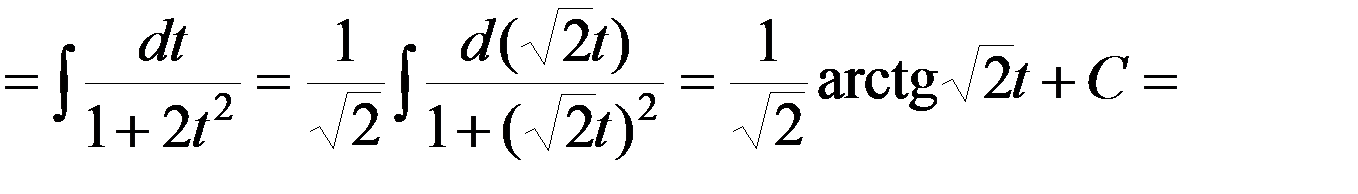
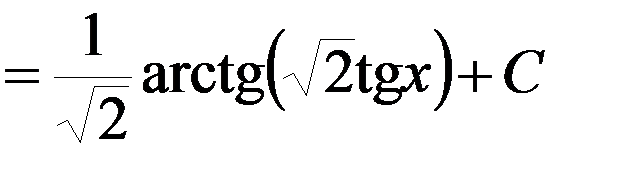 .
.
Учтено, что  .
.
▲
4.2. Интегралы типа 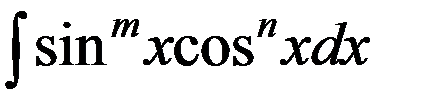
При интегрировании используются следующие приемы:
1. Подстановка sinx =t, если n=2k+1, k 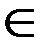 Z+.
Z+.
2. Подстановка cosx =t, если m=2k+1, k 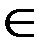 Z+.
Z+.
3. Формулы понижения порядка:
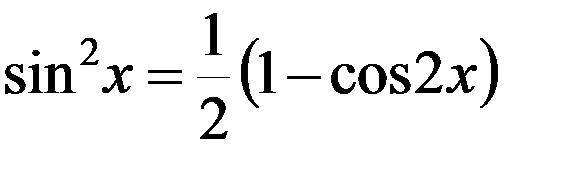 ,
,
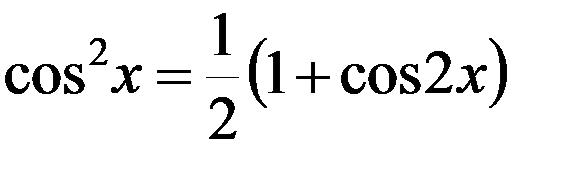 ,
,
 ,
,
если m=2k, n=2k, k 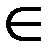 Z+.
Z+.
4. Подстановка tgx =t, если m +n =2k, k 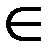 Z-.
Z-.
Пример 3.Найти интеграл
 .
.
Решение▼

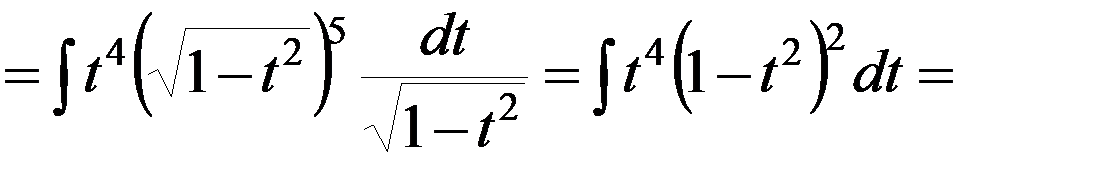
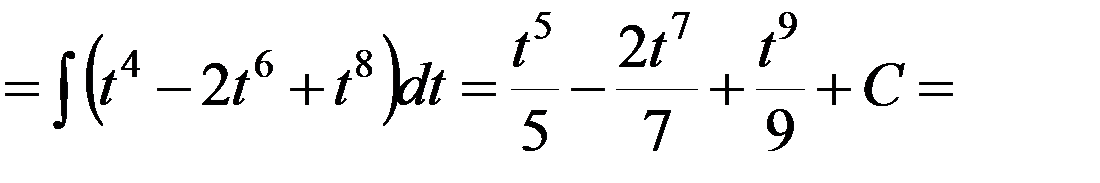
 .
.
▲
Пример 4.Найти интеграл
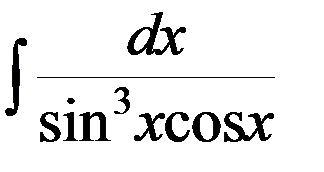 .
.
Решение▼m + n = –4.
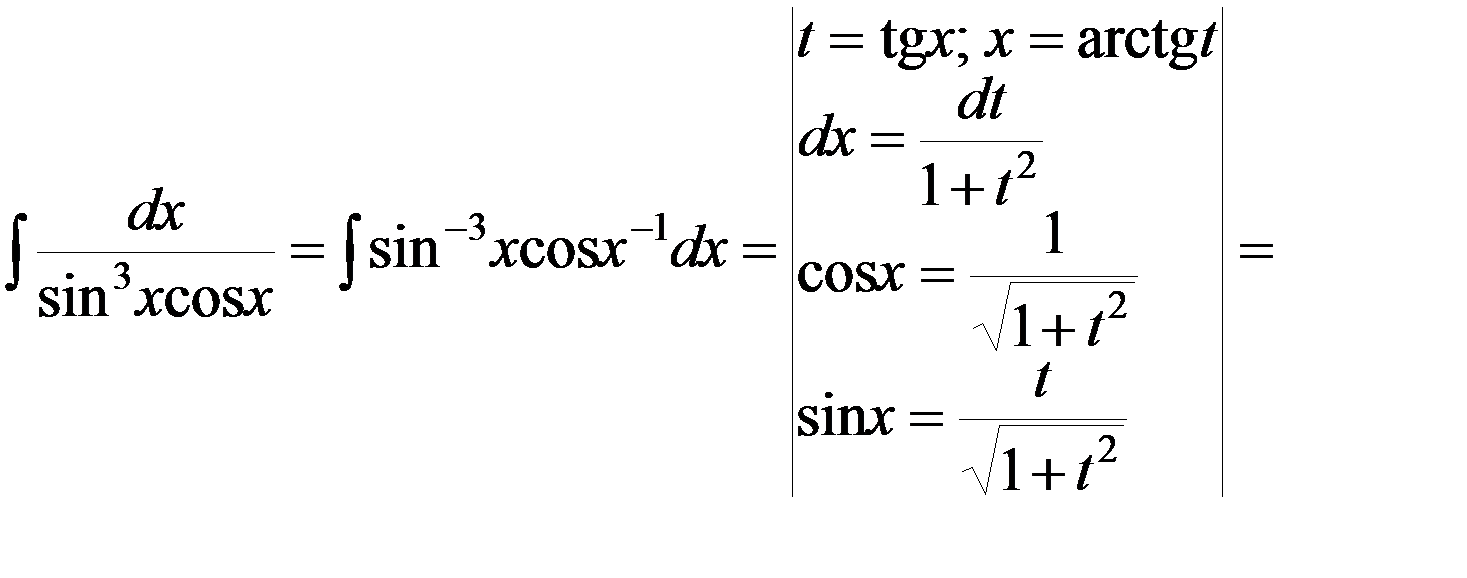
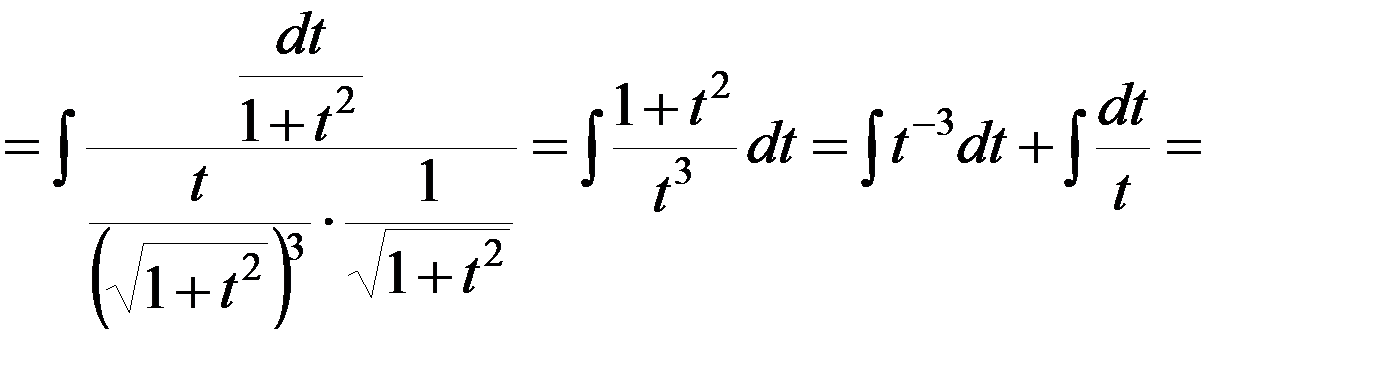
 .
.
▲