 |
|
Определение нормалей к поверхности
Остался нерешенным вопрос, каким образом в пиксельный шейдер передавать данные о нормали к поверхности. Точнее передавать их несложно, но откуда их брать? Дело в том, что данные нашей модели содержат лишь координаты вершин, нормалей там нет. Чтобы было более понятно посмотрим на рисунок части поверхности:
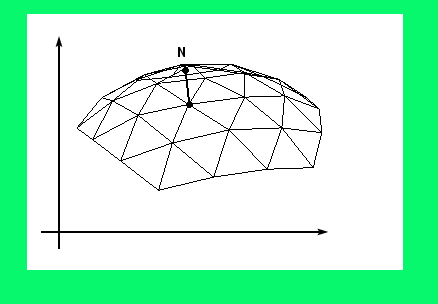
Наша задача для каждой вершины поверхности найти нормаль N. Видно, что каждая точка поверхности соединяется с шестью соседними. Эти соседние вершины соединяются треугольниками таким образом, что образуют сложную выпуклую структуру и провести к ней точно перпендикуляр несколько проблематично.
Для решения этой задачи зададимся вопросом: а насколько просто или сложно провести нормаль не к вершине, а к полигону, то есть к произвольному треугольнику поверхности. Решим эту задачу математически. Итак, имеется треугольник с набором вершин n1n2 и n3. Он образует плоскость. Необходимо определить перпендикуляр N к этой плоскости .

Решим задачу:

Таким образом, чтобы вычислить нормаль к полигону, нужно векторно умножить вектор n1n2 на вектор n1n3. Результатом такой операции получается вектор. Результирующий вектор перпендикулярен двум исходным. Чтобы окончательно решить задачу, остается только нормализовать нормали, так как полигоны могут быть различные по размеру и мы не хотим чтобы вектора нормалей тоже «скакали» по размеру. Приведенную выше формулу можно сразу перевести в код для нашей программы. Этот код мы будем использовать в приложении, а не в шейдере, так как в шейдере каждый раз рассчитывать нормали не имеет смысла. Мы можем один раз рассчитать их для нашей модели и затем использовать столько раз сколько понадобиться в шейдере.
| XMFLOAT3 n[3]; XMFLOAT3 polynormal; polynormal=XMVec3Cross(n[0]-n[1],n[0]-n[2]); polynormal=XMVec3Normalize(polynormal); |
Исходными данными является массив из трех точек n[]. Это координаты полигона. Выходящими данными является нормализованный вектор polynormal– искомая нормаль к полигону. Теперь вернемся к рисунку нашей поверхности X. Как вы думаете, будет ли нормаль из вершины поверхности смотреть в туже сторону что и нормали из центров полигонов? Ответ – безусловно. Кроме того, Если вычислить среднее направление всех соседних с вершиной нормалей к полигонам, мы и получим искомую нормаль к вершине.
Здесь и пригодится то, что мы предварительно нормализовали вектора нормалей – если бы они были разные по размеру, вычисление среднего вектора дало бы непредсказуемый результат.
Итак, окончательно имеем, что нормаль к каждой вершине равна среднему значению из нормалей всех прилегающих к вершине полигонов:

Хотя исходные данные для формулы несколько векторов N, вычисление среднего значения можно сделать также как и с обычными числами. Из урока 3 мы помним, что если вектор представить как одно число, то обнаружится много общего между числами и векторами. Таким образом, у векторов тоже определена операция вычисления среднего значения. Остается отметить, что прилегающих к произвольной вершине полигонов не всегда ровно 6, это видно из рисунка поверхности X, если обратить внимание на вершины по краям фигуры. Если количество прилегающих полигонов меньше, то мы просто в формулу вместо 6 ставим количество прилегающих к вершине полигонов.
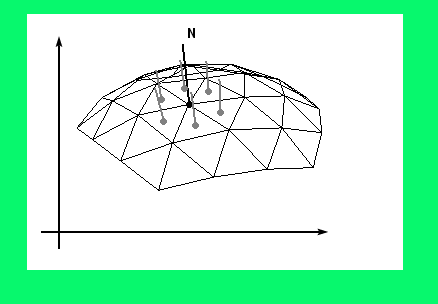
На рисунке показан результат который мы получили: Вы видите, что результирующая нормаль к вершине имеет направление среднее из нормалей всех прилегающих к ней полигонов. На рисунке нормаль к вершине имеет большую длину чем остальные, но это для наглядности, на самом деле длины одинаковые.