Главная | Обратная связь

Маршрут, ланцюг, цикл у неорієнтованому графі

Маршрутом у графі G=(V,E) між вершинами u та v графу G називається послідовність вершин даного графу виду u₁,…,u_n, де u₁=u, u_n=v, (u_i,u_i+1)ÎE, 1£i£n-1, nÎN⁺ (тобто кожні дві сусідні вершини послідовності суміжні). Маршрутом у графі G=(V,E) називається послідовність вершин даного графу виду u₁,…,u_n, де (u_i,u_i+1)ÎE, 1£i£n-1, nÎN⁺. Вершину маршруту, що не є першою чи останньою, назвемо внутрішньою вершиною. Якщо між вершинами u та v графу G існує маршрут u₁,…,u_n, будемо говорити, що вершини u та v з’єднані (сполучені) маршрутом, або маршрут u₁,…,u_n з’єднує вершини u та v, або вершина v досяжна з вершини u.

Маршрут u₁,…,u_n у графі G називається циклічним (або замкнутим), якщо u₁=u_n.

Довжиною маршруту u₁,…,u_n у графі G будемо називати число n-1, тобто число, що на одиницю менше кількості елементів у послідовності u₁,…,u_n. Маршрут, що складається з однієї вершини, називається тривіальним. Довжина тривіального маршруту дорівнює нулю.

Нехай, наприклад, задано граф G=({1,2,3,4,5},{(1,2),(2,3),(3,4),(4,5), (5,2),(5,3)}). Розглянемо таку послідовність вершин цього графу: 2,3,5,2,3. Перевіримо, чи суміжні кожні дві сусідні вершини цієї послідовності. Маємо: (2,3) – ребро графу G; (3,5), (5,2), (2,3) – також ребра графу G. Таким чином, послідовність вершин 2,3,5,2,3 є маршрутом між вершинами 2 та 3 у графі G. Довжина цього маршруту дорівнює чотирьом. Послідовність вершин графу G виду 2,5,4,3 також є маршрутом між вершинами 2 та 3 в G. Розглянемо іншу послідовність вершин даного графу: 1,3,5,4,2. Вона не є маршрутом у графі G, оскільки не кожні дві сусідні вершини цієї послідовності суміжні. Дійсно, вершини 1 та 3 – сусідні у даній послідовності, але вони не суміжні, оскільки у графі G немає ребра (1,3). Прикладом тривіального маршруту у графі G є послідовність 4. Приклади циклічних маршрутів у графі G: 1,2,3,2,1, а також 2,5,4,3,2.

Як видно з наведених прикладів, дві вершини графу можуть сполучатися кількома різними маршрутами. Зокрема, вершини 2 та 3 з’єднані маршрутом 2,3,5,2,3 та маршрутом 2,5,4,3.

Нехай G=(V,E) – граф. За кожним нетривіальним маршрутом виду u₁,u₂,u₃…,u_n-2,u_n-1,u_n у графі G визначається послідовність ребер виду (u₁,u₂),(u₂,u₃),…,(u_n-2,u_n-1),(u_n-1,u_n), у якій кожні два сусідні ребра суміжні. Наприклад, за маршрутом a,b,c,d у графі ({a,b,c,d},{(a,b),(a,d),(b,b),(b,c), (c,d)}) визначається послідовність суміжних ребер виду (a,b),(b,c),(c,d).

Маршрут u₁,…,u_n між вершинами u та v графу G називається ланцюгом між u та v, якщо у послідовності ребер, що визначається даним маршрутом, усі ребра попарно різні. Маршрут u₁,…,u_n у графі G називається ланцюгом, якщо у послідовності ребер, що визначається даним маршрутом, усі ребра попарно різні. Ланцюг u₁,…,u_n називається циклом, якщо u₁=u_n й n>1. Ланцюг u₁,…,u_n між вершинами u та v графу G називається простим, якщо усі його вершини, крім, можливо, першої та останньої, попарно різні. Ланцюг u₁,…,u_n у графі G називається простим, якщо усі його вершини, крім, можливо, першої та останньої, попарно різні. Простий ланцюг u₁,…,u_n називається простим циклом, якщо u₁=u_n й n>1. Граф без циклів назвемо ациклічним.

Наприклад, у графі G=({1,2,3,4,5},{(1,2),(2,3),(3,4),(4,5),(5,2),(5,3)}) маршрут 2,3,4,5,3 є ланцюгом між вершинами 2 та 3. Для перевірки побудуємо послідовність ребер, що визначається цим маршрутом. Маємо: (2,3), (3,4), (4,5), (5,3). Бачимо, що у цій послідовності усі ребра попарно різні. Даний ланцюг не є циклом, оскільки перша та остання вершини у ньому різні. Не є він також й простим ланцюгом (отже, не є простим циклом), адже вершина 3 входить у нього як внутрішня та як остання вершина. Розглянемо інший маршрут між вершинами 2 та 3 у графі G, а саме 2,5,4,3. Він є простим ланцюгом, оскільки, по-перше, у послідовності ребер (2,5), (5,4), (4,3), що визначається цим маршрутом, усі ребра попарно різні (тобто даний маршрут є ланцюгом), а, по-друге, вершини не повторюються. Маршрут 3,5,4,3 у графі G є циклом, а також простим циклом. Перевіримо це. Спочатку покажемо, що даний маршрут є циклом. Побудуємо послідовність ребер, що визначається цим маршрутом: (3,5),(5,4),(4,3). Бачимо, що усі ребра у послідовності попарно різні. Отже, даний маршрут є ланцюгом. Оскільки перша та остання вершини цього ланцюга однакові, він є циклом. Усі вершини цього циклу, крім першої та останньої, як бачимо, попарно різні. Таким чином, даний цикл є простим. Оскільки граф G має цикл, то він не є ациклічним. Прикладом ациклічного графу є граф ({1,2,3},{(3,1),(2,1)}).

Сформулюємо кілька тверджень, що безпосередньо випливають з наведених вище означень.

Твердження 1. Якщо у графі G існує маршрут між вершинами u та v, то у G існує маршрут між вершинами v та u.

Доведення. Нехай u₁,…,u_n – деякий маршрут між вершинами u та v у графі G. Розглянемо послідовність виду u_n,…,u₁, що утворюється, якщо записати вершини даного маршруту у зворотному порядку. Кожні дві сусідні вершини у цій послідовності суміжні, оскільки ті вершини, що були сусідніми у початковій послідовності (а, отже, й суміжними), залишаються сусідніми й у новій послідовності. Оскільки u₁=u, а u_n=v, то нова послідовність u_n,…,u₁ – маршрут між вершинами v та u у графі G. Твердження доведено.

Твердження 2. Нехай у графі G існує маршрут між вершинами u та v. Тоді у G існує простий ланцюг між вершинами u та v.

Доведення. Нехай u₁,…,u_n – деякий маршрут між вершинами u та v у графі G. Можливі два випадки: 1) даний маршрут є простим ланцюгом, 2) даний маршрут не є простим ланцюгом. У першому випадку сформульоване твердження правильне. Розглянемо другий випадок. Якщо цей маршрут не є простим ланцюгом, то існує принаймні одна вершина (назвемо її w), яка входить у послідовність u₁,…,u_n хоча б двічі, причому не лише як перша та остання. Тоді знайдуться такі числа i та j (1£i£n, 1£j£n), що u_i =w, u_j=w, причому принаймні одне з цих чисел більше 1 та менше n, й, крім того, між u_i та u_j немає входжень вершини w. Можливі такі три випадки: а) i=1, 1<j<n, б) 1<i<n, 1<j<n, в) 1<i<n, j=n. У випадку а) маємо: w=u_j=u₁=u, отже, якщо з послідовності u₁,…,u_n вилучити підпослідовність u₁,…,u_j-1, то послідовність, що залишиться (тобто u_j,…,u_n), буде маршрутом між вершинами u та v, але матиме менше входжень вершини w. У випадку б) маємо: вершини w та u_i+1 суміжні (адже w=u_i) й вершини w та u_j+1 також суміжні (адже w=u_j), отже, якщо з послідовності u₁,…,u_n вилучити підпослідовність u_i+1,…,u_j, то послідовність, що залишиться (тобто u₁,…,u_i,u_j+1…,u_n), буде маршрутом між вершинами u та v, але матиме менше входжень вершини w. У випадку в) маємо: w=u_i=u_n=v, отже, якщо з послідовності u₁,…,u_n вилучити підпослідовність u_i+1,…,u_n, то послідовність, що залишиться (тобто u₁,…,u_i), буде маршрутом між вершинами u та v (адже w=u_i=u_n=v), але матиме менше входжень вершини w. Оскільки початкова послідовність u₁,…,u_n скінченна, то виконавши описані вище перетворення скінченну кількість разів, матимемо маршрут між вершинами u та v, у якому усі вершини, крім, можливо, першої та останньої, попарно різні, тобто простий ланцюг між вершинами u та v. Твердження доведено.

Твердження 3. Нехай у графі G існує цикл. Тоді у G існує простий цикл.

Доведення. Нехай u₁,…,u_n – деякий цикл у графі G. Можливі два ви-падки: 1) даний цикл простий, 2) даний цикл не є простим. У першому ви-падку сформульоване твердження правильне. Розглянемо другий випадок. Якщо даний цикл не простий, то послідовність ребер (u₁,u₂),…,(u_n-1,u_n), що визначається послідовністю u₁,…,u_n, містить принаймні два однакові ребра, скажімо (u_i,u_i+1) та (u_j,u_j+1), i<j. Оскільки ребро неорієнтованого графу – це неупорядкована пара вершин, то з рівності ребер (u_i,u_i+1)=(u_j,u_j+1) випливають рівності u_i=u_j, u_i+1=u_j+1 або рівності u_i=u_j+1, u_i+1=u_j. Нехай u_i=u_j, u_i+1=u_j+1. Тоді вершини u_i та u_j+1 суміжні. Вилучивши з послідовності u₁,…,u_n підпослідовність u_i+1,…,u_j, маємо послідовність u₁,…u_i,u_j+1,…,u_n, яка є циклом у графі G (адже вершини u_i,u_j+1 суміжні), але такий цикл має менше пар однакових ребер, ніж початковий цикл. Нехай тепер u_i=u_j+1, u_i+1=u_j. Вилучимо з послідовності u₁,…,u_n підпослідовність u_i+1,…,u_j+1; маємо послідовність u₁,…u_i,u_j+2,…,u_n, яка є циклом у графі G. У даному випадку також зменшується кількість попарно однакових ребер порівняно з початковим циклом. Отже, виконавши описані перетворення скінченну кількість разів, матимемо цикл у графі G, що не містить попарно однакових ребер, тобто простий цикл. Твердження доведено.

Зауважимо, що коли між вершинами u та v у деякому графі існує нетривіальний маршрут, то множина маршрутів між цими вершинами нескінченна, але множина маршрутів певної заданої наперед довжини між даними двома вершинами графу скінченна. Для обчислення кількості маршрутів заданої довжини k між вершинами графу скінченного порядку використовується матриця, що є результатом піднесення матриці суміжності цього графу до k-го степеня.

Теорема 1. Нехай G=(V,E) – граф порядку n, V={v₁,…,v_n}, A_G – матриця суміжності графу G, v_i,v_j – вершини G. Тоді кількість маршрутів довжини k між вершинами v_i та v_j у графі G дорівнює числу, що знаходиться на перетині i-го рядка та j-го стовпчика k-го степеня матриці A_G.

Доведення здійснюється індукцією за числом k (kÎN⁺).

Позначимо k-й степінь матриці A_G через A_G^k, а число, що знаходиться на перетині i-го рядка та j-го стовпчика матриці A_G^k – через a_ij^(k). Розглянемо випадок k=1. Треба перевірити, чи дорівнює число a_ij⁽¹⁾ кількості маршрутів довжини 1 між i-ю та j-ю вершинами у графі G. Зауважимо, що A_G¹=A_G, отже, a_ij⁽¹⁾=a_ij. За означенням матриці суміжності, a_ij=1, якщо i-а й j-а вершини графу G суміжні, а a_ij=0, якщо ці вершини не суміжні. Але суміжність i-ї та j-ї вершин означає, що між ними існує маршрут довжини 1 у графі G, а несуміжність цих вершин означає, що маршруту довжини 1 між ними немає. Таким чином, для k=1 твердження теореми правильне.

Припустимо тепер, що твердження теореми правильне для довільного цілого додатного числа m, й покажемо, що тоді це твердження правильне й для числа m+1, тобто покажемо, що кількість маршрутів довжини m+1 між вершинами v_i та v_j у графі G дорівнює числу, що знаходиться на перетині i-го рядка та j-го стовпчика (m+1)-го степеня матриці A_G. За правилом обчислення матриці A_G^m+1 маємо: A_G^m+1=A_G^m´A_G. Тоді a_ij^(m+1)= 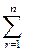a_ir^(m)´a_rj⁽¹⁾. Розглянемо окремий доданок цієї суми, тобто число a_ir^(m) ´ a_rj⁽¹⁾. За припущенням індукції a_ir^(m) є кількістю маршрутів довжини m між i-ю та r-ю вершинами у графі G. Оскільки a_rj⁽¹⁾=a_rj, то a_rj⁽¹⁾ приймає значення 1 або 0. Якщо a_rj⁽¹⁾=1, то це означає, що вершини r-а й j-а суміжні, й тоді кожен маршрут довжини m між i-ю та r-ю вершинами у графі G можна продовжити до такого маршруту довжини m+1 між i-ю та j-ю вершинами у графі G, що r-а вершина є у цьому маршруті перед-останньою. Кількість таких маршрутів дорівнює a_ir^(m)´a_rj⁽¹⁾=a_ir^(m)´1=a_ir^(m). Якщо a_rj⁽¹⁾=0, то вершини r-а й j-а несуміжні, а це означає, що жоден маршрут між i-ю та r-ю вершинами у графі G не можна продовжити до такого маршруту довжини m+1 між i-ю та j-ю вершинами у графі G, що r-а вершина є у цьому маршруті передостанньою, а a_ir^(m)´a_rj⁽¹⁾=a_ir^(m)´0=0. Кількість маршрутів довжини m+1 між i-ю та j-ю вершинами у графі G матимемо, якщо знатимемо для кожного числа r (1£r£n) кількість таких маршрутів довжини m+1 між i-ю та j-ю вершинами у графі G, що r-а вершина є у кожному з цих маршрутів передостанньою, а потім обчислимо 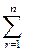a_ir^(m) ´ a_rj⁽¹⁾, тобто a_ij^(m+1). Отже, число a_ij^(m+1) є кількістю маршрутів довжини m+1 між i-ю та j-ю вершинами у графі G. Теорему доведено.

Розглянемо приклад. Знайдемо кількість маршрутів довжини три у графі G=({a,b,c,d},{(a,b),(a,c),(b,b),(b,c),(b,d),(c,d)}) між вершинами b та c. Граф G має порядок 4, отже, ми можемо занумерувати його вершини чис-лами 1, 2, 3, 4 й позначити їх таким чином: v₁=a, v₂=b, v₃=с, v₄=d. З урахуванням уведених позначень початкову задачу можна сформулювати так: знайти кількість маршрутів довжини три у графі G між 2-ю та 3-ю вер-шинами. За теоремою 1, шукана кількість маршрутів – це елемент а₂₃⁽³⁾ матриці А_G³ (А_G – матриця суміжності графу G). Маємо: а₂₃⁽³⁾=(а₂₁⁽²⁾´а₁₃⁽¹⁾)+ +(а₂₂⁽²⁾´а₂₃⁽¹⁾)+(а₂₃⁽²⁾´а₃₃⁽¹⁾)+(а₂₄⁽²⁾´а₄₃⁽¹⁾)=(а₂₁⁽²⁾´а₁₃)+(а₂₂⁽²⁾´а₂₃)+(а₂₃⁽²⁾´а₃₃)+ +(а₂₄⁽²⁾´а₄₃). (Нагадаємо, що a_ij – елемент матриці А_G й a_ij⁽¹⁾=a_ij, i,jÎ{1,2,3,4}). Знайдемо елементи а₁₃, а₂₃, а₃₃, а₄₃ матриці А_G. Маємо: а₁₃=1, оскільки вершини v₁ та v₃ суміжні (дійсно, v₁=a, v₃=c, а у графі є ребро (a,c)), a₂₃=1, оскільки суміжні вершини v₂ та v₃, тобто вершини b та c (бачимо, що у графі G є ребро (b,c)), а₃₃=0, адже v₃=с, а граф G не має петлі (с,с), а₄₃=1, оскільки вершини d та c суміжні (v₄=d, v₃=c, граф G має ребро (c,d)). Таким чином, а₂₃⁽³⁾=(а₂₁⁽²⁾´1)+(а₂₂⁽²⁾´1)+(а₂₃⁽²⁾´0)+(а₂₄⁽²⁾´1)= =а₂₁⁽²⁾+а₂₂⁽²⁾+а₂₄⁽²⁾. Нам залишилося знайти а₂₁⁽²⁾, а₂₂⁽²⁾, а₂₄⁽²⁾. Маємо:

а₂₁⁽²⁾=(а₂₁⁽¹⁾´а₁₁⁽¹⁾)+(а₂₂⁽¹⁾´а₂₁⁽¹⁾)+(а₂₃⁽¹⁾´а₃₁⁽¹⁾)+(а₂₄⁽¹⁾´а₄₁⁽¹⁾)=а₂₁´а₁₁ + а₂₂´а₂₁ + + а₂₃´а₃₁ + а₂₄´а₄₁ = 1´0 + 1´1 + 1´1 + 1´0 = 2;

а₂₂⁽²⁾=(а₂₁⁽¹⁾´а₁₂⁽¹⁾)+(а₂₂⁽¹⁾´а₂₂⁽¹⁾)+(а₂₃⁽¹⁾´а₃₂⁽¹⁾)+(а₂₄⁽¹⁾´а₄₂⁽¹⁾)=а₂₁´а₁₂ + а₂₂´а₂₂ + + а₂₃´а₃₂ + а₂₄´а₄₂ = 1´1 + 1´1 + 1´1 + 1´1 = 4;

а₂₄⁽²⁾=(а₂₁⁽¹⁾´а₁₄⁽¹⁾)+(а₂₂⁽¹⁾´а₂₄⁽¹⁾)+(а₂₃⁽¹⁾´а₃₄⁽¹⁾)+(а₂₄⁽¹⁾´а₄₄⁽¹⁾)=а₂₁´а₁₄ + а₂₂´а₂₄ + + а₂₃´а₃₄ + а₂₄´а₄₄ =1´0 + 1´1 + 1´1 + 1´0 = 2.

Таким чином, а₂₃⁽³⁾=2+4+2=8. Отже, існує 8 маршрутів довжини три у графі G між вершинами b та c.

 

Зв’язність графу

Граф G=(V,E) називається зв’язним, якщо для будь-якої пари вершин u та v графу G існує маршрут між u та v у графі G.

Зауваження. З даного означення випливає, що для перевірки зв’язності графу достатньо переконатися у тому, що для будь-яких різних вершин u та v у цьому графі існує маршрут між u та v (адже для будь-якої пари однакових вершин маршрут завжди існує: це тривіальний маршрут). До того ж, коли знайдено маршрут між вершинами u та v у графі G, то, як випливає з твердження 1, існує й маршрут між вершинами v та u у цьому графі.

Розглянемо приклади. Нехай задано граф G₀=({1,2,3,4},{(1,2),(2,3), (2,4)}). Перевіримо, чи є він зв’язним. Згідно із наведеним вище зауваженням потрібно розглянути такі пари вершин графу G₀: 1 й 2, 1 й 3, 1 й 4, 2 й 3, 2 й 4, 3 й 4 – та перевірити, чи сполучені якимось маршрутом у графі G₀ вершини кожної пари. Між вершинами 1 та 2 існує маршрут 1,2 (граф G₀ має ребро (1,2)), між вершинами 1 та 3 існує маршрут 1,2,3 (граф G₀ має ребра (1,2) та (2,3)), між вершинами 1 та 4 є маршрут 1,2,4 (граф G₀ має ребра (1,2) та (2,4)) між вершинами 2 та 3 існує маршрут 2,3 (граф G₀ має ребро (2,3)) між вершинами 2 та 4 існує маршрут 2,4 (граф G₀ має ребро (2,4)), між вершинами 3 та 4 існує маршрут 3,2,4 (граф G₀ має ребра (2,3) та (2,4)). Таким чином, граф G₀ зв’язний.

Граф G₁=({1,2,3,4},{(1,2),(1,3)}) не є зв’язним, адже не для кожної пари його вершин існує маршрут, що сполучає ці вершини. Зокрема, не існує маршруту між вершинами 1 й 4, оскільки вершина 4 ізольована (адже її степінь дорівнює нулю), тому не існує жодного нетривіального маршруту у графі G₁, що містить вершину 4, а, значить, й маршруту між вершинами 1 та 4.

Граф G₂=({1,2,3,4},{(1,2),(4,3)}) також незв’язний, оскільки у ньому немає маршруту між вершинами 2 та 3. З твердження 2 випливає, що якщо у графі немає простого ланцюга між вершинами u та v цього графу, то між u та v не існує й маршруту. Покажемо, що у G₂ немає простого ланцюга між вершинами 2 та 3. Для цього досить побудувати усі прості ланцюги у графі G₂, що починаються вершиною 2, й переконатися у тому, що серед них немає простого ланцюга, що завершується вершиною 3. Побудову будемо виконувати таким чином. Спочатку візьмемо простий ланцюг, що починається вершиною 2 й має найменшу можливу довжину. Це є ланцюг виду 2 (він має довжину 0). Потім розглянемо усі можливості продовжити цей ланцюг до простого ланцюга довжини 1. Це можна зробити, знайшовши усі вершини графу G₂, що суміжні з вершиною 2. Така вершина у даному графі лише одна (це вершина 1), отже, поки можна побудувати єдиний простий ланцюг (а саме ланцюг 2,1), що починається вершиною 2. Продовжити даний ланцюг до простого ланцюга більшої довжини ми не можемо, адже вершина 1 суміжна лише з вершиною 2, але послідовність 2,1,2 не є простим ланцюгом. Отже, ми побудували усі прості ланцюги у графі G₂, які починаються вершиною 2, й бачимо, що простого ланцюга між вершинами 2 та 3 у графі G₂ немає. Таким чином, показано, що граф G₂ незв’язний.

Нехай G – граф порядку n. Матрицею досяжності графу G (позначається D_G) називається квадратна матриця порядку n над множиною {0,1}, елемент d_ij якої дорівнює 1, якщо існує маршрут між i-ю та j-ю вершинами (1£i£n, 1£j£n) у даному графі, й дорівнює 0 у протилежному випадку, тобто коли жодного маршруту між цими вершинами у графі G немає.

Зауважимо, що з твердження 1 випливає симетричність матриці досяжності графу відносно головної діагоналі.

Побудуємо матриці досяжності графів G₀, G₁, G₂, що розглядалися вище. Позначимо ці матриці D₀, D₁, D₂ відповідно. Оскільки ми вже з’ясували, що граф G₀ є зв’язним, то його матриця досяжності D₀ містить лише одиниці; вона зображена на рис.4,а. У графі G₁ є ізольована вершина (вершина 4), тому елементи у четвертому рядку й четвертому стовпчику матриці досяжності D₁ цього графу дорівнюють нулю, крім діагонального елементу d₄₄. Оскільки вершини 1,2 суміжні, вершини 1,3 суміжні, а між вершинами 2 та 3 у графі G₁ існує маршрут 2,1,3, то решта елементів матриці D₁ – це одиниці. Матриця D₁ зображена на рис.4,б. У графі G₂ немає маршруту між такими парами вершин: 1,3; 1,4; 2,3; 2,4. Отже, лише елементи d₁₃, d₃₁, d₁₄, d₄₁, d₂₃, d₃₂, d₂₄, d₄₂ матриці досяжності D₂ графу G₂ дорівнюватимуть нулю, а решта елементів – одиниці. Матриця D₂ зображена на рис.4,в.

 

а)	б)	в)
	Рис. 4

 

Щойно ми будували матриці досяжності графів, безпосередньо перевіряючи для пар різних вершин графу наявність маршруту між ними. Але існує інший спосіб побудови матриці досяжності графу скінченного порядку. Цей спосіб ґрунтується на використанні матриці суміжності графу та двох бінарних операцій на множині {0,1} (позначаються Ù, Ú). Операція Ù визначається такими співвідношеннями: 0Ù0=0Ù1=1Ù0=0, 1Ù1=1. Операція Ú визначається співвідношеннями виду: 0Ú0=0, 1Ú0=0Ú1=1Ú1=1.

Визначимо тепер бінарні операції Ù, Ú (кон’юнкції та диз’юнкції) на множині квадратних матриць порядку n над множиною {0,1}. Нехай А, В такі матриці. Через АÙВ позначимо квадратну матрицю порядку n, елемент c_ij (1£i£n, 1£j£n) якої обчислюється таким чином:

c_ij = (a_i1Ùb_1j)Ú(a_i2Ùb_2j)Ú…Ú(a_inÙb_nj).

Через АÚВ позначимо квадратну матрицю порядку n, елемент m_ij (1£i£n, 1£j£n) якої обчислюється таким чином: m_ij = a_ijÚb_ij.

Розглянемо приклади. Нехай А= , В= . Обчислимо спочатку матрицю М=АÚВ. Маємо: m₁₁=a₁₁Úb₁₁=0Ú1=1, m₁₂=a₁₂Úb₁₂=1Ú1=1, m₂₁=a₂₁Úb₂₁=0Ú1=1, m₂₂=a₂₂Úb₂₂=1Ú0=1. Отже, M= . Тепер обчислимо матрицю С=АÙВ. Маємо: с₁₁=(a₁₁Ùb₁₁)Ú(a₁₂Ùb₂₁)=(0Ù1)Ú(1Ù1)=0Ú1=1,

c₁₂=(a₁₁Ùb₁₂)Ú(a₁₂Ùb₂₂)=(0Ù1)Ú(1Ù0)=0Ú0=0,

c₂₁=(a₂₁Ùb₁₁)Ú(a₂₂Ùb₂₁)=(0Ù1)Ú(1Ù1)=0Ú1=1,

c₂₂=(a₂₁Ùb₁₂)Ú(a₂₂Ùb₂₂)=(0Ù1)Ú(1Ù0)=0Ú0=0.

Таким чином, С= .

Нехай G – граф порядку n, A_G – матриця суміжності графу G. Визначимо матрицю A_G^(k) таким чином:

Твердження 4. Нехай G – граф порядку n. Маршрут довжини k (k³1) між i-ю та j-ю вершинами графу G існує тоді й тільки тоді, коли елемент a_ij^(k) матриці A_G^(k) дорівнює одиниці.

Доведення аналогічне доведенню теореми 1.

Твердження 5. Нехай G – граф порядку n, матриця D визначена та-ким чином: D=Е_nÚA_G⁽¹⁾ÚA_G⁽²⁾Ú…ÚA_G⁽ⁿ⁾ (тут Е_n – одинична матриця поряд-ку n). Тоді маршрут між i-ю та j-ю вершинами у графі G існує тоді й тільки тоді, коли елемент d_ij матриці D дорівнює одиниці.

Доведення. (Þ) Нехай між i-ю та j-ю вершинами (1£i£n, 1£j£n) у графі G існує маршрут. Якщо i=j, то d_ij=1, оскільки у матриці Е_n e_ij=1Ûi=j. Нехай i¹j. Тоді, згідно з твердженням 2, між цими вершинами у G існує простий ланцюг. Оскільки граф G має n вершин, то довжина будь-якого простого ланцюга у G (отже, й простого ланцюга між i-ю та j-ю вершинами графу G) не перевищує n. Тоді, за твердженням 4, існує таке ціле число k (1£k£n), що елемент a_ij^(k) матриці A_G^(k) дорівнює одиниці. Отже, й d_ij=1.

(Ü) Нехай d_ij=1 (1£i£n, 1£j£n). Покажемо, що між i-ю та j-ю верши-нами у графі G існує маршрут. Зауважимо, що при i=j між i-ю та j-ю вер-шинами у графі G існує тривіальний маршрут. Нехай i¹j. З умови d_ij=1 та з означення матриці D випливає, що для деякого цілого k (1£k£n) елемент a_ij^(k) матриці A_G^(k) дорівнює одиниці. А це означає, що між i-ю та j-ю вершинами у графі G існує маршрут довжини k, а, значить, дійсно існує маршрут між цими вершинами у G. Твердження доведено.

Наслідок. Матриця D збігається з матрицею досяжності графу G.

Граф H=(V₁,E₁) називається підграфом графу G=(V,E), якщо V₁ÍV, E₁ÍE. Граф H=(V₁,E₁) називається власним підграфом графу G=(V,E), якщо виконується одна з умов: 1) V₁ÌV, E₁ÍE, 2) V₁ÍV, E₁ÌE, 3) V₁ÌV, E₁ÌE.

З даного визначення випливає, що кожен граф має принаймні один підграф. (Дійсно, якщо G=(V,E) – граф, то, оскільки VÍV та EÍE, G є підграф G.) Якщо граф G має не один підграф, то усі підграфи графу G, крім самого G, є його власними підграфами. (Дійсно, для підграфу H=(V₁,E₁) графу G=(V,E), що не є його власним підграфом, має виконуватися умова V=V₁, E=E₁, але тоді H=G.)

Підграф H=(V₁,E₁) графу G=(V,E) називається кістяковим підграфом G, якщо V₁=V.

Розглянемо приклади. Граф G₁=({1,2,4},{(1,2)}) є підграфом графу G=({1,2,3,4},{(1,2),(1,3),(2,3),(3,4)}), оскільки множина вершин {1,2,4} графу G₁ є підмножиною множини вершин {1,2,3,4} графу G, а множина ребер графу G₁ є підмножиною множини ребер графу G (дійсно, {(1,2)}Í{(1,2),(1,3),(2,3),(3,4)}). Граф G₂=({1,2,3,4},{(1,2),(1,3),(3,4)}) та-кож є підграфом графу G. Дійсно, для множин вершин графів G₂ та G маємо: {1,2,3,4}={1,2,3,4}, отже, {1,2,3,4}Í{1,2,3,4}; для множин ребер графів G₂ та G маємо: {(1,2),(1,3),(3,4)}Í{(1,2),(1,3),(2,3),(3,4)}. Графи G₁ та G₂ є власними підграфами графу G. Граф G₂ є кістяковим підграфом графу G, а граф G₁ – ні. Граф G₃=({0,1,2,3},{(1,2),(1,3),(2,3)}) не є підгра-фом графу G, оскільки множина його вершин містить вершину 0, якої немає у множині вершин графу G, а тому не включається у множину вершин графу G.

Максимальним зв’язним підграфом графу G називається такий його зв’язний підграф, який не є власним підграфом жодного зв’язного підграфу графу G. Максимальний зв’язний підграф графу G будемо називати компонентом зв’язності графу G.

Нехай, наприклад, H=({a,b,c,d},{(a,d),(a,c)}); діаграма графу H подана на рис.5,a. Компонентами зв’язності H є такі його підграфи: H₁=({a,c,d},{(a,d),(a,c)}), H₂=({b},Æ) (рис.5,б,в). Обґрунтуємо це тверджен-ня. Для цього побудуємо усі зв’язні підграфи графу H та покажемо, що ні H₁, ні H₂ не є власним підграфом жодного з побудованих підграфів. Отже, зв’язними підграфами графу H (крім H₁ та H₂) є такі графи: H₃=({a},Æ), H₄=({c},Æ), H₅=({d},Æ), H₆=({a,d},{(a,d)}), H₇=({a,c},{(a,c)}). Бачимо, що граф H₁ не є підграфом (а, значить, й власним підграфом) жодного з графів H₂, H₃, H₄, H₅, H₆, H₇, оскільки множина вершин {a,c,d} не є підмножиною множини вершин жодного з цих графів. Граф H₂ також не є підграфом (а, значить, й власним підграфом) жодного з графів H₁, H₃, H₄, H₅, H₆, H₇, бо множина вершин {b} не є підмножиною множини вершин жодного з цих графів. Таким чином, H₁ та H₂ – компоненти зв’язності графу H. Покажемо тепер, що інших компонентів зв’язності граф H не має. Для цього достатньо переконатися у тому, що кожен зв’язний підграф H, крім, звичайно, H₁ та H₂, є власним підграфом деякого зв’язного підграфу графу H. Таку перевірку потрібно здійснити для графів H₃, H₄, H₅, H₆, H₇. Бачимо, що граф H₃ є власним підграфом зв’язного графу H₆, тому що для множин вершин та множин ребер цих графів маємо відповідно: {a}Ì{a,d}, ÆÌ{(a,d)}; аналогічним чином переконуємося, що H₅ є власним підграфом H₆, а H₄, H₆ та H₇ – власними підграфами H₁. Отже, граф H не має компонентів зв’язності, відмінних від H₁ та H₂.

 

а)	б)	в)
	Рис. 5

 

Зауважимо, що єдиним компонентом зв’язності будь-якого зв’язного графу G є сам граф G, оскільки будь-який зв’язний підграф графу G, відмінний від G, є власним підграфом графу G (тобто не є максимальним зв’язним підграфом графу G).

Теорема 2. Будь-який незв’язний граф єдиним чином подається у вигляді диз’юнктивного об’єднання усіх своїх компонентів зв’язності.

Доведення. Нехай G=(V,E) – незв’язний граф. Розглянемо бінарне відношення R на множині вершин V графу G:

uRv Û існує маршрут між u та v у графі G.

Дане відношення є рефлексивним (uRu для будь-якої вершини u графу G, оскільки існує тривіальний маршрут між u та u у G), симетричним (uRv Þ між u та v існує маршрут у графі G Þ між v та u існує маршрут у G Þ vRu), транзитивним (uRv,vRw Þ між u та v існує маршрут у G, скажімо, u₁,…,u_k, де u=u₁, v=u_k; між v та w існує маршрут у G, скажімо, v₁,…,v_m, де v=v₁, w=v_m Þ між u та w існує маршрут у G, а саме u₁,…u_k-1,v₁,…,v_m Þ uRw). Отже, R є відношенням еквівалентності на множині V. Тоді існує розбиття множини V на непорожні підмножини V₁,…,V_n,…, що визначається відношенням R. Зауважимо, що це розбиття містить більше однієї множини (якби це було не так, то усі вершини графу G потрапили б в одну множину V₁, а це означало б, що для будь-яких вершин u та v графу G існує маршрут між u та v, тобто граф G зв’язний). Для кожної множини V_i даного розбиття побудуємо граф G_i=(V_i,E_i), де E_i={(u,v)|u,vÎV_i, (u,v)ÎE}). Кожен такий граф G_i є підграфом графу G, адже V_iÍV, E_iÍЕ. Покажемо, що G=G₁È…ÈG_nÈ…. Для цього достатньо показати, що V=V₁È…ÈV_nÈ…, E=E₁È…ÈE_nÈ…. Доведемо першу рівність. Нехай uÎV. Тоді знайдеться деяка множина V_i розбиття множини V, що містить u. Отже, VÍV₁È…ÈV_nÈ…. Нехай uÎV₁È…ÈV_nÈ…. Тоді вершина u належить деякій множині V_i розбиття множини V, але, оскільки V_iÍV, то uÎV. Таким чином, V=V₁È…ÈV_nÈ…. Доведемо другу рівність. Нехай (u,v)ÎE. Це означає, що між u та v існує маршрут (довжини 1), а тоді u та v належать одному й тому самому класу розбиття V_i множини вершин V. За побудовою E_i, (u,v)ÎE_i, й тоді (u,v)ÎE₁È…ÈE_nÈ…. Таким чином, EÍE₁È…ÈE_nÈ…. Нехай тепер (u,v)ÎE₁È…ÈE_nÈ…. Тоді (u,v) є елементом деякої множини E_i, але оскільки E_iÍE, то (u,v)ÎE, отже, E₁È…ÈE_nÈ….ÍE. Таким чином, E=E₁È…ÈE_nÈ…. Отже, G=G₁È…ÈG_nÈ…. Оскільки V₁,…,V_n,…– розбиття множини V, то при i¹j множини V_i та V_j не мають спільних елементів. Ми довели, що граф G подається у вигляді диз’юнктивного об’єднання своїх підграфів. Кожен з цих графів є зв’язним за побудовою. Залишилося показати, що кожен підграф G_i цього об’єднання є компонентом зв’язності G. Припустимо супротивне. Тоді у об’єднанні G₁È…ÈG_nÈ… існує хоча б один граф (позначимо його G_i), що не є максимальним зв’язним підграфом графу G. Це означає, що існує такий зв’язний підграф G_х=(V_x,E_x) графу G, що V_iÌV_x або E_iÌE_х. У випадку V_iÌV_x у графі G існує така вершина x, що xÎV_x, хÏV_i, x досяжна з будь-якої вершини множини V_i. Але за побудовою V_і вершина х має належати V_i. Отже, маємо суперечність. Таким чином, наше припущення про те, що V_iÌV_x, неправильне, а тоді V_i=V_x. Розглянемо випадок E_iÌE_х. З даного строгого включення випливає, що у G існує ребро (y,z) таке, що (y,z)ÎE_х, а (y,z)ÏE_i. Оскільки V_i=V_x, то y,zÎV_i, й, за побудовою G_i, ребро (y,z) має належати E_i. Отже, E_i=E_х. Таким чином, G_i=G_х. Тоді G_i – максимальний зв’язний підграф графу G. Оскільки відношення R визначається графом G однозначно (це видно з побудови R), розбиття V₁,…,V_n,…, а також й компоненти зв’язності G_i,…,G_n… визначаються однозначно, то G дійсно єдиним чином подається у вигляді диз’юнктивного об’єднання усіх своїх компонентів зв’язності. Теорему доведено.

Теорема 3. Граф G=(V,E) зв’язний тоді й тільки тоді, коли G не можна подати у вигляді диз’юнктивного об’єднання двох його підграфів.

Доведення. (Þ) Нехай граф G зв’язний. Припустимо, що існує подання G у вигляді диз’юнктивного об’єднання двох його підграфів, тобто G=G₁ÈG₂, де G₁=(V₁,E₁), G₂=(V₂,E₂), причому V₁ÇV₂=Æ, V₁¹Æ, V₂¹Æ. Нехай uÎV₁, vÎV₂. Тоді, оскільки граф G зв’язний, між u та v існує нетривіальний маршрут, а, значить, й простий ланцюг. У цьому ланцюзі є ребро, один кінець якого належить V₁, а інший – V₂, але це неможливо, бо V₁ÇV₂=Æ. Отже, наше припущення неправильне, й зв’язний граф G не можна подати у вигляді диз’юнктивного об’єднання двох його підграфів.

(Ü) Нехай G=(V,E) – такий граф, який не можна подати у вигляді диз’юнктивного об’єднання двох його підграфів. Покажемо, що G зв’язний. Припустимо супротивне. Тоді у графі G є принаймні дві вершини (позначимо їх u та v), між якими немає маршруту. Визначимо такі підмножини множини V: V_u={w| існує маршрут між u та w у G}, V_v={w| існує маршрут між v та w у G}, V_x={w| wÏV_u, wÏV_v}. Множина V_u непорожня: вона містить принаймні вершину u й усі ті вершини, що досяжні з u (якщо такі вершини існують). Аналогічним чином побудована множина V_v також непорожня (vÎV_v); множина V_x може бути порожньою. З означення множин V_u, V_v, V_x випливає, що V_v Ç V_u=Æ, V_uÇV_x=Æ, V_v Ç V_x=Æ. Побудуємо графи G₁=(V_v,E₁), G₂=(V_uÈV_x,E₂), E₁={(v₁,v₂)| v₁,v₂ÎV_v, (v₁,v₂)ÎE}, E₂={(u₁,u₂)| u₁,u₂ÎV_uÈV_x, (u₁,u₂)ÎE}. Оскільки V_vÍV, E₁ÍE, V_uÈV_xÍV, E₂ÍE, то G₁, G₂ – підграфи графу G. Покажемо, що G=G₁ÈG₂. Для цього достатньо показати, що V=V_vÈV_uÈV_x, E=E₁ÈE₂. За побудовою множин V_v, V_u, V_x, V_vÈV_uÈV_xÍV. Нехай wÎV. Для вершини w можливі такі випадки: 1) w досяжна з v, й тоді vÎV_v; 2) w не досяжна з v, й тоді wÎV_u або wÎV_x. У кожному з цих випадків wÎV_vÈV_uÈV_x. Отже, VÍV_vÈV_uÈV_x. Таким чином, V=V_vÈV_uÈV_x. Зауважимо, що множини V_v, V_u, V_x утворюють розбиття множини V. За побудовою множин E₁, E₂, маємо E₁ÈE₂ÍE. Нехай (y,z)ÎE. Для вершини y можливі такі випадки: 1) yÎV_v, 2) yÏV_v. Якщо yÎV_v, то zÎV_v, адже z досяжна з y. Але тоді (y,z)ÎE₁. Якщо yÏV_v, то yÎV_u або yÎV_х. Якщо yÎV_u, то zÎV_u, але тоді (y,z)ÎE₂. Якщо yÎV_х, то z не може належати ні V_v, ні V_u, отже, zÎV_х, але тоді (y,z)ÎE₂. Таким чином, (y,z)ÎE₁ÈE₂, отже, EÍE₁ÈE₂. Ми довели, що E=E₁ÈE₂. Оскільки V_v Ç(V_uÈV_x)=Æ, то граф G подано у вигляді диз’юнктивного об’єднання двох його підграфів. Отже, маємо суперечність, а це означає, що наше припущення про незв’язність G неправильне. Таким чином, G зв’язний. Теорему доведено.