 |
|
Оптическая фильтрация пространственных частот
ИССЛЕДОВАНИЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ В ОПТИКЕ
Цель работы: исследование дифракции и фильтрации изображения в когерентном свете, определение периода решетки (транспаранта).
оборудование: лабораторный оптический комплекс ЛКО-1Э сгазовым гелий-неоновым лазером; набор модулей: № 3 (проекционный микроскоп), № 5 (входная оптика), № 9 (кассета), № 6 (тонкая линза f= +100 мм), № 10(кассета в поворотном держателе); экран № 1 – калибровочная сетка 1,00 мм, экран № 18 – круглое отверстие, экраны № 23, 24 – щели d= 0,5 и d=1,0 мм, экраны № 31 и 32––решетки линейные d= 0,3 и d=0,6 мм (транспаранты), 34 и 35 ––решетки двумерные прямоугольная и косоугольная (транспаранты).
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Анализ сложного волнового поля во многих случаях целесообразно проводить, разлагая его на простейшие составляющие, например, представляя его в виде разложения по плоским волнам. При этом оказывается, что если мы рассматриваем поле, полученное после прохождения плоской монохроматической волны через предмет или транспарант (изображение предмета на фотоплёнке или стеклянной пластинке) с функцией пропускания t(x), то разложение по плоским волнам соответствует преобразованию Фурье от этой функции. Если за предметом поставить линзу, то каждая плоская волна сфокусируется в свою точку в задней фокальной плоскости линзы. Таким образом, картина, наблюдаемая в фокальной плоскости линзы, даёт нам представление о спектре плоских волн падающего на линзу волнового поля. Поэтому можно утверждать, что с помощью линзы в оптике осуществляется пространственное преобразование Фурье.
Оптическая фильтрация пространственных частот
Рассмотрим оптический метод, широко применяемый в автоматике для получения результатов сложных математических операций и для распознавания образов, что существенно в науке, технике и медицине.
В основе теории этого метода лежат преобразования Фурье, частным случаем которых является представление функций в виде рядов и интегралов Фурье. Напомним, что интегральное представление функции F(t) выражается в виде:
F(t)= 
f(()ei(td(, (1)
где
f(()=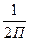
F(t) e-i(tdt, (2)
Функция f(() называется Фурье-образом или Фурье-преобразованием функции F (t). Еe смысл состоит в том, что произведение f(() выражает зависимость амплитуды в спектральном представлении функции F (t) от частоты в условиях непрерывного спектра частот.
Рассмотрим функцию двух переменных F (x,у). Эта функция может быть представлена на фотопластинке, экспонированной таким образом, что после проявления прозрачность в окрестности каждой точки пропорциональна значению функции в этой точке. В целях упрощения и большей ясности в последующем изложении положение точек на этой пластинке будет обозначаться буквой МО и функция будет записываться как F (MО). Допустим, что в некоторых местах пластинки имеются периодически повторяющиеся элементы изображения, например, прямолинейные отрезки (рис.1). Число таких элементов, приходящихся на единицу длины направления, вдоль которого происходит их повторение, называется пространственной частотой этих элементов. На рис. 1 представлены две таких частоты: (1= N1/l1 и (2= N2/l2, где N1и N2 — число элементов в периодических сериях.
На рис. 2 приведена схема двойной дифракции, посредством которой осуществляется метод оптической фильтрации. На рисунке показано взаимное расположение когерентного источника S, двух линз L1и L2, и трех плоскостей ПО, ПС,, ПИ , выполняющих главную роль в работе схемы. Сами же дифрагирующие лучи на рисунке не изображены. Положение точек в плоскости ПОбудем обозначать буквойМО , в плоскости ПС буквой (.
|
В плоскости ПОустанавливается фотопластинка с представленной на ней функцией F (М0). Она освещается сходящимся световым пучком, прошедшим через линзу L1. При прохождении через пластинку пучок рассеивается за счет дифракции на неоднородностях прозрачности пластинки, выражающих запись на ней функции F (MО). Математический анализ этой дифракции приводит к выводу, что дифрагированный пучок создает в плоскости ПС, проходящей через изображение источника S линзой L1, распределение амплитуд, описываемое функцией f((), пропорциональной интегралу:
f(() ( 
F (M0)е(i(МоdМо (3)
Сопоставив это с соотношением (2), видим, что f(() представляет собой Фурье-образ функции F (M0). Следовательно, каждой точке ( в плоскости Пс соответствует некоторое значение пространственной частоты и потому распределение амплитуд дифрагированного света в этой плоскости выражает спектральное представление функции F (МО) в условиях непрерывного спектра частот. Поэтому плоскость Пс называется спектральной плоскостью (Фурье-плоскостью), а плоскость По — плоскостью объекта.
Изображение одномерной амплитудной решётки и её спектр, формирующийся в плоскости Пс, показаны на рис. 3.
Рис 3. Одномерная амплитудная решётка (а) и её пространственный спектр (б) в виде дифракционной картины в плоскости Пс
В спектральной плоскости может располагаться фотопластинка, обработанная так, что на ней представлена некоторая функция Н((). Эта пластинка называется фильтром. Очевидно, что существует функция J(М0), по отношению к которой H (() является ее Фурье-образом. То есть, если в плоскости объекта ПО поместить фотопластинку, на которой представлена функция J (М), то дифрагированный свет создаст в плоскости Пс распределение амплитуд, сооттветсвующее функции фильтра H((). В методе оптической фильтрации особую роль выполняют фильтры, для которых функция H(() представляет распределение амплитуд в изображении точечного источника света, расположенного в центре плоскости ПО. Такая функция называется импульсной реакцией системы.
Таким образом, в спектральной плоскости Пс имеет место взаимное наложение спектрального распределения функции F(М0), выраженного Фурье-образом f(() и функции фильтра H((). В результате возникает объединенная спектральная функция (((), выражаемая как
((()=f(() H(() (4)
При прохождении через фильтр световой пучок вновь испытывает рассеяние за счет дифракции. После прохождения через линзу L2 дифрагированный пучок создает изображение (распределение амплитуд), которое может быть выражено некоторой функцией G (М). Оказывается, что эта функция является интегральным представлением Фурье типа (1), в котором роль спектральной функции выполняет произведение (4):
G (M) = f(() H(()е-i(МоdМо (5)
Это соотношение и лежит в основе метода оптической фильтрации. Функция G (М) в той или иной форме содержит информацию о математических операциях над совокупностью функций F (M) и J (M), Фурье-образы которых представлены в (5). Например, если Н (() представляет вышеупомянутую импульсную реакцию системы, то G (M) выражается следующим образом:
G (М) = F (Мo) J (М - М0) dM0.(6)
Интегралы вида (6) называются интегральными свертками функций, они играют важную роль в математике. Таким образом, метод оптической фильтрации, в частности, позволяет получать свертки функций. При этом функции не обязательно должны иметь аналитические выражения. Например, функция F(Mo) может быть задана таблицей или номограммой. Этоже соотношение (6) лежит в основе автоматического распознавания образов. Допустим, что в плоскости ПО последовательно помещаются пластинки, на каждой из которых представлены изображения множества различных объектов. Требуется установить, имеется ли на какой-либо пластинке изображение отыскиваемого объекта и в каком месте пластинки это изображение находится. С этой целью изготовляется специальный фильтр с чертами нужного объекта.
Теперь рассмотрим случай, когда на расположенной в плоскости объекта пластинке имеются наборы периодически повторяющихся по прозрачности элементов с соответствующими пространственными частотами (рис. 1). Очевидно, что каждому такому набору в спектральной плоскости соответствует точка, положение которой определяется частотой набора (. В принципиальном отношении дифракция света на периодическом наборе элементов подобна дифракции на решетке с синусоидальной пропускаемостью. Из условия максимума для дифракции на такой решетке следует, что чем меньше период решетки d=l/N и чем, стало быть, больше пространственная частота (=1/d, тем больше угол отклонения дифрагированного пучка. Отсюда следует, что чем больше частота периодического набора элементов на пластинке, тем больше точка, соответствующая этой частоте в спектральной плоскости, удалена от оси симметрии оптической системы. Причем направление, в котором сдвинута от оси эта точка, совпадает с направлением на пластинке, вдоль которого происходит периодическое повторение элементов. Для того, чтобы в плоскости ПИ получить изображение набора с пространственной частотой (, надо в плоскость ПС поместить фильтр в виде узкой прозрачной полоски, проходящей через точку ( и ориентированной вдоль направления повтора элементов. Если же в спектральную плоскость поместить фильтр в виде прозрачного круга, за пределами которого прозрачности нет, то будут пропущены только те частоты, точки которых лежат в пределах круга. В результате в плоскости ПИ будет получена картина, соответствующая объекту после исключения из него пространственных гармоник, частоты которых лежат за пределами фильтрующего круга. Другие виды фильтров исключат из изображения объекта другие наборы частот.
Рассмотрим обработку изображений с помощью простейших фильтров. В качестве одного из примеров использования низкочастотной фильтрации могут быть эксперименты Аббе (1873 г.) и Портера (1906 г.) – первые опыты по пространственной фильтрации изображений [1]. Используем транспарант в виде двумерной амплитудной решётки с прямоугольным профилем штриха (рис. 4, а). В плоскости фильтрации формируется пространственный двумерный спектр решётки в виде дифракционной картины в плоскости Пс, показанной на рис. 4, б.
Рис. 4 . Двумерная решетка (а) и ее пространственный спектр (б)
Если с помощью щели выделить только часть спектра, соответствующую одномерной решётке (см. рис. 3, а), то в плоскости Пс, на выходе оптического процессора (устройства, осуществляющего оптическое преобразование Фурье) получится изображение одномерной решётки (см. рис. 3, б). Важно отметить, что в этих условиях направление штрихов в изображении, перпендикулярном оси щели, зависит только от наклона оси щели, но не от направления штрихов в исходном транспаранте.
Вторым примером использования низкочастотного фильтра может служить метод исправления помех малого размера на изображении с крупными деталями. Мелкими помехами могут быть царапины, точки, «снег» на изображении или периодическая структура самого транспаранта, как в случае типографского способа его изготовления. Поскольку в этих случаях пространственный спектр шумов лежит в высокочастотной области, низкочастотный фильтр оказывается эффективным для их подавления, как показано на рис. 5.
Рис.5 . Отстройка от «снега» с помощью низкочастотного фильтра: а – объект с помехой, б – спектр объекта с помехой, в – низкочастотный фильтр, г – отфильтрованное изображение объекта.
Таким образом, с помощью линзы в оптике осуществляется пространственное преобразование Фурье: при освещении транспаранта плоской монохроматической волной картина, наблюдаемая в задней фокальной плоскости линзы, установленной за транспарантом, представляет собой фурье-образ функции пропускания транспаранта. Можно доказать, что если транспарант установлен в передней фокальной плоскости линзы, то в её задней фокальной плоскости восстанавливаются и амплитудные, и фазовые соотношения между плоскими волнами, и таким образом строго осуществляется комплексное фурье-преобразование.
Во многих практически важных случаях функция пропускания транспаранта чисто амплитудная, как, например, в случае решётки. Тогда для того, чтобы найти фурье-образ функции пропускания транспаранта, достаточно определить только пространственные частоты и соотношение между амплитудами плоских волн на выходе из транспаранта. Интересно заметить, что наблюдаемая визуально картина фраунгоферовой дифракции в задней фокальной плоскости линзы не зависит от расстояния между транспарантом и линзой, так как глаз не реагирует на фазу волны, а регистрирует только интенсивность (усреднённый по времени квадрат амплитуды поля). Условия наблюдения дифракции Фраунгофера можно выполнить и без применения линзы, если наблюдать дифракционную картину на достаточно удалённом экране. Таким образом, пространственное преобразование Фурье может осуществляться и в свободном пространстве при наблюдении дифракции Фраунгофера.