Главная | Обратная связь

Двойственность в линейном программировании

Двойственный симплекс-метод решения задач ЛП

 

С каждой задачей линейного программирования тесно связана другая задача, называемая двойственной; первоначальная задача называется исходной или прямой. Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой. Однако при определении симплекс–методом оптимального плана одной из задач автоматически находится решение и другой задачи.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

1) если целевая функция исходной задачи формулируется на максимум, то целевая функция двойственной задачи – на минимум, и наоборот. При этом в задаче на максимум во всех неравенствах в функциональных ограничениях используется знак « », а в задаче на минимум − знак « »;

2) матрицы коэффициентов при неизвестных в системах ограничений прямой и двойственной задач получаются друг из друга транспонированием;

3) число неизвестных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе у двойственной задачи – числу неизвестных в исходной;

4) коэффициенты при неизвестных в целевой функции двойственной задачи являются свободными членами в системе ограничений прямой задачи, а свободные члены в системе ограничений двойственной задачи есть коэффициенты целевой функции прямой задачи;

5) каждому ограничению прямой задачи соответствует неизвестная двойственной: номер неизвестной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства со знаком « », соответствует неизвестная, связанная условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая неизвестная двойственной задачи может принимать как положительные, так и отрицательные значения;

6) задача, двойственная двойственной, совпадает с исходной;

7) базисным неизвестным прямой задачи линейного программирования соответствуют свободные неизвестные двойственной, и наоборот.

Математические модели пары двойственных задач могут быть симметричными и несимметричными.

В несимметричных двойственных задачах система ограничений исходной задачи задаётся в виде равенств, в двойственной – в виде неравенств, причём в последней неизвестные могут быть и отрицательными.

В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи, задаётся неравенствами, причём на двойственные неизвестные налагается условие неотрицательности.

Везде далее будем рассматривать только симметричные взаимо-двойственные задачи линейного программирования.

Запишем пару симметричных взаимодвойственных задач линейного программирования в соответствии с перечисленными выше правилами (табл. 9.1).

Таблица 9.1

Прямая задача линейного программирования	Двойственная задача линейного программирования

 

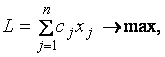
Основные утверждения о взаимодвойственных задачах линейного программирования содержатся в следующих теоремах.

Первая теорема двойственности. Для пары взаимодвойственных задач линейного программирования имеет место один из следующих взаимоисключающих случаев:

1. В прямой и двойственной задачах линейного программирования имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:

2. В прямой задаче линейного программирования множество допустимых решений не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи линейного программирования будет пустое множество допустимых решений.

3. В двойственной задаче линейного программирования множество допустимых решений не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи линейного программирования множество допустимых решений оказывается пустым.

4. Обе задачи из пары взаимодвойственных задач линейного программирования имеют пустые множества допустимых решений.

Вторая теорема двойственности (принцип дополняющей нежёсткости). Пусть допустимое решение прямой задачи линейного программирования, а допустимое решение двойственной задачи линейного программирования. Для того чтобы эти решения были оптимальными решениями соответствующих взаимодвойственных задач линейного программирования, необходимо и достаточно того, чтобы выполнялись следующие равенства:

(9.1)

(9.2)

Замечание.

Условия (9.1) и (9.2) позволяют, зная оптимальное решение одной из взаимодвойственных задач линейного программирования, найти оптимальное решение другой задачи.

Для решения взаимодвойственных задач линейного программирования используется двойственный симплекс-метод, один из способов реализации которого рассмотрим на следующем примере.

Пример.Найти оптимальное решение стандартной задачи минимизации для целевой функции

с ограничениями

при условиях неотрицательности

 

 

Составить двойственную задачу и записать её оптимальное решение.

Решение.Составим задачу, двойственную данной, пользуясь сформулированными выше правилами (или табл. 9.1).

Поскольку прямая задача линейного программирования − задача минимизации, то двойственная задача − это задача максимизации; её целевая функция имеет вид:

 

система ограничений записывается в виде

 

 

а неизвестные удовлетворяют условиям неотрицательности:

 

 

Приведём прямую и двойственную задачи линейного программирования к каноническому виду, вводя дополнительно в их системы ограничений неотрицательные балансовые неизвестные (в прямую задачу):

 

 

и (в двойственную задачу):

 

 

В прямой и двойственной задачах базис усматривается сразу:

− для задачи минимизации:

− для задачи максимизации: .

Следует отметить, что задача минимизации не имеет предпочтительного вида в базисе

Установим соответствие неизвестных прямой и двойственной задач линейного программирования. Для этого воспользуемся тем фактом, в соответствии с которым базисным неизвестным прямой задачи соответствуют свободные неизвестные двойственной, а свободным неизвестным прямой задачи – базисные неизвестные двойственной. Для данной задачи это соответствие изображено на рис. 9.1.

Поскольку задача максимизации в базисе имеет предпочтительный вид, составим для неё начальную симплекс-таблицу (табл. 9.2), добавив дополнительную строку неизвестных задачи максимизации, учитывая установленное соответствие неизвестных.