 |
|
Алгоритм шифрования данных IDEA.
Алгоритм IDEA (International Data Encryption Algorithm) является блочным шифром. Он оперирует 64-битовыми блоками открытого текста. Несомненным достоинством алгоритма IDEA является то, что его ключ имеет длину 128 бит. Один и тот же алгоритм используется и для шифрования, и для расшифрования. Первая версия алгоритма IDEA была предложена в 1990 г., ее авторы – Х.Лей и Дж.Мэсси. Как и большинство других блочных шифров, алгоритм IDEA использует при шифровании процессы смешивания и рассеивания, причем все процессы легко реализуются аппаратными и программными средствами.
В алгоритме IDEA используются следующие математические операции:
1) поразрядное сложение по модулю 2 (операция "исключающее ИЛИ"); операция обозначается как (+)
2) сложение беззнаковых целых по модулю 2^16 (модуль 65536); операция обозначается как |+
3) умножение целых по модулю (2^16+1) (модуль 65537), рассматриваемых как беззнаковые целые, за исключением того, что блок из 16 нулей рассматривается как 2^16; операция обозначается как (.)
Все операции выполняются над 16-битовыми субблоками.
Следующие три операции несовместимы в том смысле, что:
1) никакая пара из этих трех операций не удовлетворяет ассоциативному закону,
например a |+| (b (+) c) != (a |+| b) (+) c
2) никакая пара из этих трех операций не удовлетворяет дистрибутивному закону,
например a (.) (b |+| c) != (a |+| b) (.) (a |+| c)
Комбинирование этих трех операций обеспечивает комплексное преобразование входа, существенно затрудняя криптоанализ IDEA по сравнению с DES, который базируется исключительно на операции "исключающее ИЛИ".
Общая схема алгоритма IDEA приведена на рисунке
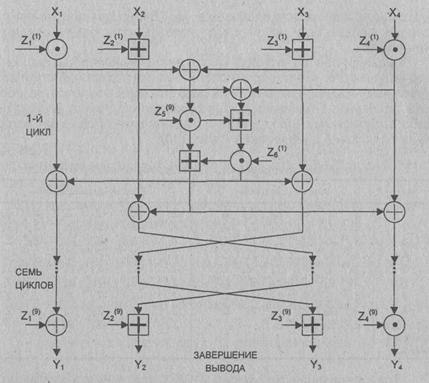
64-битовый блок данных делится на четыре 16-битовых субблока. Эти четыре субблока становятся входом в первый цикл алгоритма. Всего выполняется восемь циклов. Между циклами второй и третий субблоки меняются местами. В каждом
цикле имеет место следующая последовательность операций:
(1) (.) – умножение субблока Х1 и первого подключа.
(2) |+| – сложение субблока Х2 и второго подключа.
(3) |+| – сложение субблока Х3 и третьего подключа.
(4) (.) – умножение субблока Х4 и четвертого подключа.
(5) (+) – сложение результатов шагов (1) и (3).
(6) (+) – сложение результатов шагов (2) и (4).
(7) (.) – умножение результата шага (5) и пятого подключа.
(8) |+| – сложение результатов шагов (6) и (7).
(9) (.) – умножение результата шага (8) с шестым подключом.
(10) |+| – сложение результатов шагов (7) и (9).
(11) (+) – сложение результатов шагов (1) и (9).
(12) (+) – сложение результатов шагов (3) и (9).
(13) (+) – сложение результатов шагов (2) и (10).
(14) (+) – сложение результатов шагов (4) и (10).
Принято предположение, что нулевой субблок 2^16 – 1, а мультипликативная обратная величина равна 0. Вычисление некоторых мультипликативных обратных величин требует некоторых затрат, но это делается всего 1 раз для каждого ключа расшифрования. Выходом цикла являются четыре субблока, которые получают как результаты выполнения
шагов (11), (12), (13) и (14). В завершение цикла переставляют местами два внутренних субблока (за исключением последнего цикла), и в результате формируется вход для следующего цикла.
X1 X2 X3 X4
Z1(1) Z2(1) Z3(1) Z4(1)
Z5(9)
1-й
цикл
Z6(1)
13
Обозначения:
Xi – 16-битовый субблок открытого текста, i = 1…4
Yi – 16-битовый субблок шифртекста, i = 1…4
Zj(r) – 16-битовый подключ (субблок ключа), j = 1…6, r = 1…8
– поразрядное суммирование по модулю 2 16-битовых субблоков
16
– сложение по модулю 2 16-битовых целых
16
– умножение по модулю 2 16-битовых целых (с нулевым субблоком,
16
соответствующим 2 )
18.03.2013
В 1985г Кобниц и Миллер предложили использовать криптографические кривые(КК) для криптографии. В 1998г использование КК для решения криптографических задач, таких как цифровая подпись, было закреплено в различных стандартах. Основное достоинство эллиптических кривых заключается в том, что по сравнению с рассмотренными нами ранее системами, они имеют более высокую стойкость при равной трудоемкости. Это объясняется тем, что для вычисления обратных функций известны только алгоритмы с экспотенциальным ростом трудоемкости, тогда как для обычных методов предложены субъэкспотенциальные методы.
…
Математические основы(элементарная математика).
Общий вид кривой задается уравнением вида:
Y^2 + a1 * X * Y + a1 * Y = X^3 + a2 * X^2 + a2 *X + a0, где ai – некоторая константа.
Кривая третьего порядка E задается уравнением вида:
E: F^2 = X^3 + a*X + b. (1)
Необходимо решить кубическое уранение.
D = 4 * a^3 + 27 * b^2.
Если D<0, то имеется 3 различных действительных корня, если D=0 – 3 действительных корня(по крайней мере 2 корня равны), если D>0 – имеется 1 действительных корень и 2 мнимых.
КАРТИНКИ(стр 5 из ссылки)
При D=0 кривая называется сингулярной, так как в точке бета имеется 2 касательные. Потому при задании кривой с помощью параметров a и b, потребуем чтобы дискриминант не был равен 0.
D != 0 (2).
Пусть эллиптическая кривая E задана уравнением F^2 = X^3 + a*X + b (1) с ограничением D != 0 (2) на его коэффициенты. Определим операцию композиции(сложения) точек на кривой. Берем 2 любые точки P(x1, y1) и Q(x2, y2) @ E. Эта прямая пересечет эллиптическую кривую в третьей точке R’. Третья точка обязательно существует, потому что мы имеем кубическое уравнение, которое получается после подстановки в уравнение прямой формулы 1. Соответственно R’ существует. Определим теперь точку R(x3, y3). Получим ее из точки R’ путем изменения знака. Данную операцию P + Q назовем композицией точек.
Пусть точка P@E имеет координаты (x, y), тогда точку с координатами (x, -y) будем обозначать -P. Проведем прямую –PP, которая пересечет эллиптическую кривую в бесконечно удаленной ночке О.
O = P +(композиция) (-P). P + O = O + P = P.
Представим себе ситуацию, в которой точка Q сближается с точкой P и сливается в одну точку, т.е. P=Q=(x1, y1).
…
Хуй пойми что за поебень
Подставим в уравнение эллиптической кривой, получим
(y1 + k * (x – x1))^2 = x^3 + a * x + b
x^3 – k^2 * x^2
Сумма корней кубического уравнения равна противоположному коэффициенту при x^2, т.е. k^2.
x1 + x2 + x3 = k^2
x3 = x1 + x2 – k^2
Подставив … найдем ординату точки R’. Изменив знак, получим y3 = (x1 – x3)
…
Рассмотрим когда P = Q и результирующая равна композиции точки P, т.е. ее удвоению.
Получаем 2yy’ = 3 * x^2 + a. Угловой коэффициент касательной равен значению производной в точке P. Дальнейшие рассуждения аналогичны ранее рассмотренным. Координаты точки R определяются по тем же формулам. Используя полученные формулы для вычисления композиции и принятые соглашения о точке в бесконечности, можно доказать следующее свойство точек на эллиптической кривой:
1) P + Q = Q + P, для всех точке P и Q @ E.
2) P + Q + S = P + Q + S, для всех точек P, Q, S @ E.
3) Существует нулевой элемент O, такой что P + O = O + P = P, для всех P @ E.
4) Для каждой точки для всех P @ E существует точка -P @ E, такая что P + (-P) = O.
Перечисленные свойства точек совпадают со свойствами целых чисел при использовании операции сложения, поэтому композицию точек иногда называют сложением, а операцию [2] P называют удвоением точки P.
По аналогии со сложением можем рассматривать операцию [m] P = P + P + … + P(m раз).
Для того чтобы использовать для криптографии эллиптические кривые… используют только операции сложения, вычитания, умножения, деления чисел. Это значит, что все приведенные выше тождества будут иметь место, если мы будем выполнять вычисления с целыми числами по модулю простого числа p. В этом случае сложение и умножение выполняются по модулю числа p. Разность u - v вычисляется как u + ( p – v) mod p. Деление u/v выполняется как u * k^v mod p.
В результате мы получим эллиптическую кривую следующего вида:
E: y^2 = x^2 + a * X + b (mod p)