 |
|
Радикальна ознака Коші
Нехай для позитивного ряду  (an ≥ 0) існує границя
(an ≥ 0) існує границя 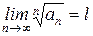 .
.
Тоді справедливі наступні твердження:
а) якщо, l < 1 те цей ряд збігається;
б) якщо, l > 1 те цей ряд розбігається.
Приклад.Дослідити на збіжність ряд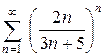 .
.
Розв‘язок. За радикальною ознакою Коші
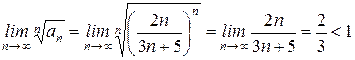 . Ряд збігається.
. Ряд збігається.
Інтегральна ознака Коші
Якщо члени позитивного ряду  можуть бути представлені як числові значення деякої безперервної монотонно спадною на проміжку [1,+∞) функції f(x) так, що
можуть бути представлені як числові значення деякої безперервної монотонно спадною на проміжку [1,+∞) функції f(x) так, що 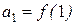 ,
, 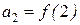 , …,
, …,  ,…, то ряд
,…, то ряд  і невласний інтеграл
і невласний інтеграл 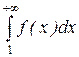 збігаються або розбігаються одночасно.
збігаються або розбігаються одночасно.
Приклади:
1.Дослідити на збіжність ряд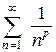 .
.
Розглянемо функцію  , для якої
, для якої  . За інтегральною
. За інтегральною
ознакою  =
=
=  .
.
2.Дослідити на збіжність ряд .
.
Розглянемо функцію  , для якої
, для якої 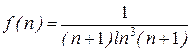 . За інтегральною ознакою
. За інтегральною ознакою

=  .
.
Знакозмінні ряди.Ряд  знакозмінний, якщо він містить нескінчен-ну множину позитивних і негативних елементів. Знакозмінний ряд
знакозмінний, якщо він містить нескінчен-ну множину позитивних і негативних елементів. Знакозмінний ряд  єабсолютно збіжним, якщо сходиться ряд
єабсолютно збіжним, якщо сходиться ряд  .
.
Достатня ознака збіжності знакозмінного ряду. Якщо збігається ряд  , складений з модулів членів ряду, то збігається і сам знакозмінний ряд
, складений з модулів членів ряду, то збігається і сам знакозмінний ряд  .
.
Знакопереміжним рядом називається ряд, для якого члени, які стоять поруч, мають різні знаки, тобто
 . (8.3)
. (8.3)
Достатня ознака збіжності знакопереміжного ряду (ознака Лейбніца) Якщо для знакопереміжного ряду :
:
1) послідовність абсолютних величин членів ряду монотонно спадає, тобто 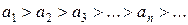 ;
;
2) загальний член ряду прямує до нуля  , то ряд збігається.
, то ряд збігається.
Функціональні ряди
Ряд називається функціональним, якщо його елементи є функціями, які визначені на одній множені Х
 (8.4)
(8.4)
Якщо при х = х0 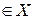 числовий ряд збігається, то точка х0 називається точкою збіжності; якщо ж ряд розбігається - точкою розбіжності функці-онального ряду.
числовий ряд збігається, то точка х0 називається точкою збіжності; якщо ж ряд розбігається - точкою розбіжності функці-онального ряду.
Степеневі ряди
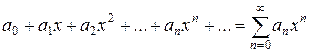 . (8.5)
. (8.5)
Області збіжності степеневого ряду (теорема Абеля).
1) Якщо степеневий ряд (8.5) збігається при x = x0 , то він збігається і притому абсолютно для усіх  ;
;
2) якщо степеневий ряд (9.3) розбігається при x = x1, то він
розбігається для усіх 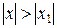 .
.
Інтервал і радіус збіжності степеневого ряду . Теорема Абеля ствер-дьжує, що якщо х0 - точка збіжності степеневого ряду, то в усіх точках, розташованих на інтервалі 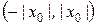 (рис 8.1а), цей ряд збігається абсолютно, а якщо х1 - точка розбіжності ряду, то в усіх точках, розташованих поза інтервалом
(рис 8.1а), цей ряд збігається абсолютно, а якщо х1 - точка розбіжності ряду, то в усіх точках, розташованих поза інтервалом 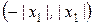 (рис. 8.1б), ряд розбігається.
(рис. 8.1б), ряд розбігається.

Рис. 8.1.
Інтервал 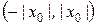 називають інтервалом збіжності степеневого ряду. Поклавши
називають інтервалом збіжності степеневого ряду. Поклавши  , інтервал збіжності можна записати у виді (- R, R). Число R називають радіусом збіжності степеневого ряду, тобто R > 0 - таке число, що при усіх |х| < R, ряд (8.5) абсолютно збігається, а при |х| > R розбігається.
, інтервал збіжності можна записати у виді (- R, R). Число R називають радіусом збіжності степеневого ряду, тобто R > 0 - таке число, що при усіх |х| < R, ряд (8.5) абсолютно збігається, а при |х| > R розбігається.
З ознаки збіжності Даламбера радіус збіжності степеневого ряду може бути визначений співвідношенням 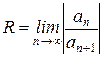 . (8.6)
. (8.6)
Приклади
1.Знайти область збіжності ряду 
Знаходимо радіус збіжності
 .
.
Отже, цей ряд збігається при будь-якому значенні х. Загальний член цього ряду прямує до нуля.

2.Знайти область збіжності ряду 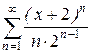
Знаходимо радіус збіжності  .
.
Отже, ряд сходиться при - 2 < x + 2 < 2, тобто при - 4 < х < 0. При х = - 4 маємо ряд 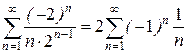 , який за ознакою Лейбніца збігається. При х = 0 маємо ряд, що розбігається
, який за ознакою Лейбніца збігається. При х = 0 маємо ряд, що розбігається 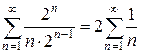 .
.
Отже, областю збіжності початкового ряду є - 4 ≤ х < 0.
3.Ряд 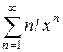 розбігається на усій числовій прямій, окрім точки х = 0, оскільки радіус збіжності
розбігається на усій числовій прямій, окрім точки х = 0, оскільки радіус збіжності  .
.
Розвинення функцій в степеневі ряди. Розвинення функції в степе-невий ряд Тейлора має вигляд

 (8.7)
(8.7)
Якщо у ряді Тейлора х0 = 0, то ряд називається рядом Маклорена, він має вигляд
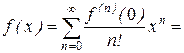
 (8.8)
(8.8)
Розвинення основних функцій в степеневі ряди:
 ,
,
 ,
,
 ,
,
 ,
,
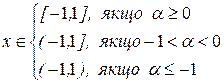 ,
,
 ,
,
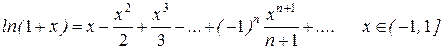 ,
,
 .
.
Ряди Фур'є. Якщо функція f(x) - періодична функція періоду 2p, неперервна на відрізку [-p; p] або вона має на цьому відрізку кінцеве число точок розриву першого роду тоді ця функція f(x) розкладається f(x) в тригонометричний ряд Фурье
 =
=  , (8.9)
, (8.9)
де 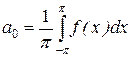 ,
, 
 ,
,
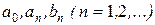 називаються коефіцієнтами коефіцієнтами Фур'є для функції f(x).
називаються коефіцієнтами коефіцієнтами Фур'є для функції f(x).
Приклад.Розкласти в ряд Фур'є періодичну функцію 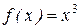 з періодом T = 2p на відрізку [-p; p].
з періодом T = 2p на відрізку [-p; p].
Задана функція є непарною, отже, коефіцієнти Фур'є шукаємо у виді:
 ,
,
де 


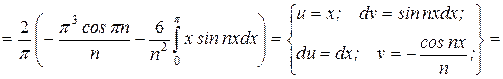

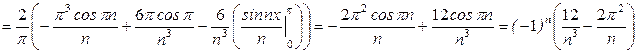
Отримуємо:  .
.
Завдання для самостійного розв‘язку
Знайти суму ряда
8.1. 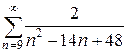 ; Відповідь: 8.2.
; Відповідь: 8.2. 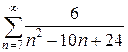 ; Відповідь:
; Відповідь:
8.3.  ; Відповідь: 8.4.
; Відповідь: 8.4. 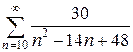 ; Відповідь:
; Відповідь:
8.5.  ; Відповідь: 8.6.
; Відповідь: 8.6. 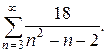 Відповідь:
Відповідь:
Дослідити на збіжність
8.7. 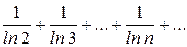 ;Відповідь: 8.8.
;Відповідь: 8.8.  ; Відповідь:
; Відповідь:
8.9.  ; Відповідь: 8.10.
; Відповідь: 8.10.  ; Відповідь:
; Відповідь:
8.11.  ; Відповідь: 8.12.
; Відповідь: 8.12. 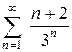 ; Відповідь:
; Відповідь:
8.13. 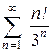 ; Відповідь: 8.14.
; Відповідь: 8.14. 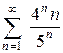 ; Відповідь:
; Відповідь:
8.15. 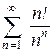 ; Відповідь: 8.16.
; Відповідь: 8.16.  . Відповідь:
. Відповідь:
8.17. 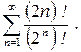 Відповідь: 8.18.
Відповідь: 8.18. 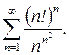 Відповідь:
Відповідь:
8.19. 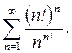 Відповідь: 8.20.
Відповідь: 8.20.  Відповідь:
Відповідь:
8.21.  Відповідь: 8.22.
Відповідь: 8.22.  Відповідь:
Відповідь:
Знайти область збіжності
8.23. 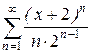 ; Відповідь: 8.24.
; Відповідь: 8.24. 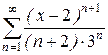 ; Відповідь:
; Відповідь:
8.25.  Відповідь: 8.26.
Відповідь: 8.26.  ; Відповідь:
; Відповідь:
8.27.  ; Відповідь: 8.28.
; Відповідь: 8.28. 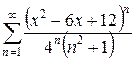 . Відповідь:
. Відповідь:
8.29. 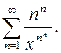 Відповідь: 8.30.
Відповідь: 8.30.  Відповідь:
Відповідь:
8.31.  Відповідь: 8.32.
Відповідь: 8.32.  Відповідь:
Відповідь:
8.33.  Відповідь: 8.34.
Відповідь: 8.34.  Відповідь:
Відповідь:
Розкласти функцію в ряд Маклорена
8.35. 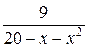 ; Відповідь:
; Відповідь:
8.36. 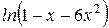 ; Відповідь:
; Відповідь:
8.37.  ; Відповідь:
; Відповідь:
8.38.  ; Відповідь:
; Відповідь:
8.39.  ; Відповідь:
; Відповідь:
8.40. 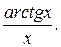 Відповідь:
Відповідь:
8.41.  Відповідь:
Відповідь:
8.42.  Відповідь:
Відповідь:
8.43.  Відповідь:
Відповідь:
8.44.  Відповідь:
Відповідь:
8.45.  Відповідь:
Відповідь:
8.46. 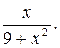 Відповідь:
Відповідь:
8.47.  Відповідь:
Відповідь:
8.48. 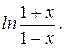 Відповідь:
Відповідь: