Главная | Обратная связь

Основные теоремы двойственности

Итак, согласно теории линейного программирования каждой задаче линейного программирования вида (3.1) - (3.3) соответствует двойственная ей задача линейного программирования вида (3.4) - (3.6). Теория двойственности в линейном программировании строится на нескольких теоремах.

Первая теорема двойственности. Если задача линейного программирования имеет конечный оптимум, то двойственная к ней также имеет конечный оптимум, и оптимальные значения линейных форм обеих задач совпадают, то есть

мax = min .

Вторая теорема двойственности (теорема о дополняющей нежесткости).Компоненты оптимального решения задачи линейного программирования равны абсолютным величинам коэффициентов при соответствующих переменных в выражении линейной формы двойственной ей задачи при достижении ею оптимума.

Пусть X = (х₁,х₂,...,х_n) — допустимое решение прямой задачи (3.1) - (3.3), а У = (у₁, у₂,…,у_m) — допустимое решение двойственной задачи (3.4) - (3.6). Для того чтобы они были оптимальными решениями соответствующих взаимодвойственных задач (3.1) - (3.3) и (3.4) - (3.6), необходимо и достаточно, чтобы выполнялись следующие соот­ношения:

; (3.7)

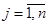; (3.8)

Иными словами, условия (3.7) и (3.8) позволяют, зная оптимальное решение одной из взаимодвойственных задач, найти оптимальное решение другой задачи.

Рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Теорема об оценках. Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений – неравенств прямой задачи на величину :

. (3.9)

Поясним смысл данной теоремы.

Пусть X = (х₁,х₂,...,х_n) – оптимальное решение прямой задачи, а У = (у₁, у₂,…,у_m) – оптимальное решение двойственной задачи. Оптимальные значения целевых функций и достигаются при подстановке компонент оптимального решения в их первоначальные выражения, т.е.

= с₁х₁ + … + c_jx_j + … + c_nx_n,

= b₁y₁ + … + b_iy_i + … b_my_m.

На основании первой теоремы двойственности можно записать

с₁х₁ + … + c_jx_j + … + c_nx_n = b₁y₁ + … + b_iy_i + … b_my_m.

Отсюда следует, что = b₁y₁ + … + b_iy_i + … b_my_m.

Если поставить вопрос о том, как изменится величина , если в исходной задаче увеличить свободный член b_i в i-м ограничении-неравенстве на величину Δ b_i, то получим следующее.

Величина , рассматриваемая теперь как функция переменных b_i получить приращение Δ . Частные производные этой функции по любому из этих аргументов имеют вид

.

Учитывая, что функция линейна, получим формулу (3.9), т.е.

.

Итак, решая задачу линейного программирования симплексным методом, мы одновременно решаем двойственную задачу. Значения переменных двойственной задачи y_i в оптимальном плане называют объективно обусловленными, или двойственными оценками.