 |
|
Свойства двойственных задач.
Двойственные задачи.
Ранее была рассмотрена задача оптимального производственного планирования. В приведенной модели 
–запас 
-го ресурса,
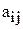– расход ресурса -го вида на единицу продукции 
-го вида,
– прибыль, получаемая при реализации единицы продукции -го вида.
Предположим, что некоторая организация решила закупить ресурсы предприятия и необходимо установить оптимальные цены на эти ресурсы 
. Покупающая организация заинтересована в том, чтобы затраты на все ресурсы 
в количествах 
были минимальными, т.е.
.
С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции 1-го вида расходуется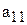 
единиц ресурса 1-го вида, 
единиц ресурса 2-го вида, и т.д. по цене соответственно . Поэтому для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции 1-го вида д.б. не менее ее цены 
, т.е.
.
Аналогично можно составить ограничения по каждому виду продукции.
В таблице приведены исходная и двойственная задачи.
Таблица 1
| Задача 1 (исходная) | Задача 2 (двойственная) |
| 
|
Цены ресурсов в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл этих названий состоит в том, что условные, «ненастоящие» цены. В отличие от «внешних» цен 
на продукцию, известных, как правило, до начала производства, цены ресурсов являются внутренними, ибо они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их называют оценками ресурсов.
Свойства двойственных задач.
1. В одной задаче ищут максимум, в другой – минимум.
2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
3. Каждая из задач задана в симметрическом виде, причем в задаче максимизации все неравенства вида « 
», а в задаче минимизации – все неравенства « 
».
4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных имеются в обеих задачах.
Пример 1. Составить задачу, двойственную к следующей задаче
Решение.
1. Приведем задачу к симметрическому виду. Для этого преобразуем систему ограничений
2. 
Составим расширенную матрицу системы
3. 
Транспонируем
4. Сформулируем двойственную задачу
Первая теорема двойственности.Если одна из двойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны:
или 
.
Если линейная функция одной из задач не ограничена, то условия другой задачи противоречивы.
Пусть даны две двойственные задачи (таблица 1). Для того, чтобы решить обе задачи симплексным методом необходимо привести их к каноническому виду. В систему ограничений задачи 1 вводим дополнительные переменные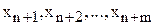 
, а в систему ограничений задачи 2 – 
.
Системы ограничений каждой из двойственных задач принимают вид:
Установим соответствие между первоначальными переменными одной из задач и дополнительными переменными другой.
| Переменные задачи 1 (исходной) | |
| первоначальные | дополнительные |
| 
|
| дополнительные | первоначальные |
| Переменные задачи 2 (двойственной) |
Теорема.Положительным (ненулевым) компонентам оптимального решения одной из двойственных задач соответствуют нулевые компоненты оптимального плана другой задачи, т.е. если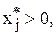 
то 
если 
то 
и аналогично, 
то 
если 
то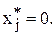 
Вторая теорема двойственности.Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.
Пример 2. Решить симплексным методом задачу
и найти оптимум и оптимальное решение двойственной задачи, используя теоремы двойственности.
Решение:
Приведем задачу к каноническому виду:
Введем искусственные переменные 
в первое и четвертое уравнения.
Получаем задачу в виде:
Составим симплексную таблицу
| БП | Св. чл. | Переменные | Оценочное отношение | |||||||
| x1 | x2 | x3 | x4 | x5 | х6 | х7 | х8 | |||
| х7 | -1 | -1 | 0,5 | |||||||
| x4 | -1 | ∞ | ||||||||
| x5 | -1 | |||||||||
| х8 | -1 | |||||||||
| Z | -2 | |||||||||
| M | 6М | -3М | М | М | М | М |
| БП | Св. чл. | Переменные | Оценочное отношение | |||||||
| x1 | x2 | x3 | x4 | x5 | х6 | х7 | х8 | |||
| х1 | 1/2 | -1/2 | -1/2 | - | ∞ | |||||
| x4 | 49/2 | 7/2 | -1/2 | - | ||||||
| x5 | 5/2 | -1/2 | 1/2 | - | ∞ | |||||
| х8 | 9/2 | 3/2 | 1/2 | -1 | - | |||||
| Z | -1/2 | -3/2 | 1/2 | - | ||||||
| M | 9/2М | -3/2М | -1/2М | М | - | М |
| БП | Св. чл. | Переменные | Оценочное отношение | |||||
| x1 | x2 | x3 | x4 | x5 | х6 | |||
| х1 | -1/3 | -1/3 | ∞ | |||||
| x4 | -5/3 | 7/3 | ||||||
| x5 | 2/3 | -1/3 | ∞ | |||||
| х2 | 1/3 | -2/3 | ∞ | |||||
| Z | -1 |
| БП | Св. чл. | Переменные | Оценочное отношение | |||||
| x1 | x2 | x3 | x4 | x5 | х6 | |||
| х1 | -4/7 | 1/7 | ||||||
| х6 | -5/7 | 3/7 | ||||||
| x5 | 3/7 | 1/7 | ||||||
| х2 | -1/7 | 2/7 | ||||||
| Z | 2/7 | 3/7 |
.
Из оценочной строки последней таблицы получаем
.
В этой задаче соотношение между переменными принимает вид
По первой теореме двойственности: 
.
По второй теореме двойственности:
Итак, в двойственной задаче 
.