 |
|
Описание экспериментальной установки
Трифилярный подвес представляет собой круглую платформу радиуса R, подвешенную на трех симметрично расположенных нитях одинаковой длины (рисунок 3). Наверху эти нити также симметрично прикреплены к диску несколько меньшего размера (радиуса r). Платформа может совершать крутильные колебания вокруг вертикальной оси OO′ , перпендикулярной к ее плоскости и проходящей через ее центр. Такое движение платформы приводит к изменению положения ее центра тяжести по высоте.

Рисунок 3 – Трифилярный подвес
Если платформа массы m, вращаясь в одном направлении, поднялась на высоту h , то приращение потенциальной энергии будет равно
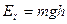 , (5)
, (5)
где g - ускорение свободного падения.
Вращаясь в другом направлении, платформа придет в положение равновесия (h=0) с кинетической энергией, равной
 , (6)
, (6)
где J - момент инерции платформы, ω0 - угловая скорость вращения платформы в момент прохождения ею положения равновесия.
Пренебрегая работой сил трения, на основании закона сохранения механической энергии имеем:
 , (7)
, (7)
Считая, что платформа совершает гармонические крутильные колебания, можно записать зависимость углового смещения j платформы от времени t в виде
 , (8)
, (8)
где j0 - угол максимального поворота платформы, т.е. амплитуда углового смещения;
T - период колебания;
 - циклическая частота колебания.
- циклическая частота колебания.
Т.к. угловая скорость ω является первой производной по времени от величины углового смещения, то
 . (9)
. (9)
В момент прохождения платформы через положение равновесия (t = 0;  ;
;  и т.д.) величина ω(t) будет максимальна и равна по модулю
и т.д.) величина ω(t) будет максимальна и равна по модулю
 . (10)
. (10)
Из выражений (7) и (10) следует, что
 . (11)
. (11)
Если l - длина нитей подвеса, R - расстояние от центра платформы до точек крепления нитей на ней, r - радиус верхнего диска (рисунок 3), то высота подъема платформы
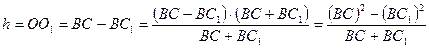 . (12)
. (12)
Так как  , то можно принять ВС + ВС1 = 2l, тогда (12) запишется в виде
, то можно принять ВС + ВС1 = 2l, тогда (12) запишется в виде
 . (13)
. (13)
Далее:
 (14)
(14)

Из  , тогда
, тогда
 . (15)
. (15)
Подставляя (14) и (15) в (13), получаем высоту подъема платформы
 . (16)
. (16)
При малых углах отклонения φ0 значение синуса угла  заменим просто значением
заменим просто значением  . Тогда (11) примет вид:
. Тогда (11) примет вид:  , откуда
, откуда
 (17)
(17)
По формуле (17) можно экспериментально определить момент инерции пустой платформы или платформы с телом, положенным на нее, так как все величины в правой части формулы непосредственно измеряются. Следует помнить, что m - это суммарная масса платформы и исследуемого тела, положенного на нее.
4. Порядок выполнения работы
1. Ознакомьтесь с параметрами системы, приведенными в таблице 2.
2. Необходимо сначала определить момент инерции J0 ненагруженной платформы. Для этого нужно сообщить прибору при помощи шнура небольшие отклонения, и измерить при помощи секундомера продолжительность некоторого числа n колебаний (n = 40 - 50). Занесите результат измерения в таблицу 2.
3. Повторите пункт 2 еще дважды.
4. Для определения момента инерции груза Jг необходимо определить момент инерции платформы вместе с грузом J=J0+Jг. Поместите груз в виде круглой пластины на платформу так, чтобы центры тяжести платформы и груза совпадали.
5. Сообщите прибору при помощи шнура небольшие отклонения, и измерьте при помощи секундомера продолжительность n колебаний. Занесите результат измерения в таблицу 3.
6. Повторите пункт 5 еще дважды.
7. Проведите опыт (пункты 4-6) для квадратной пластины.
5. Обработка результатов
1. Вычислите период колебаний ненагруженной платформы:  .
.
2. Определите среднее значение периода колебаний ненагруженной платформы.
3. По формуле (17) определите момент инерции ненагруженной платформы J0. Здесь T – средний период колебаний ненагруженной платформы, m=m0 – масса платформы.
4. Вычислите период колебаний нагруженной платформы (круглая пластина).
5. Определите среднее значение периода колебаний нагруженной платформы.
6. По формуле (17) определите момент инерции нагруженной платформы. Здесь T – средний период колебаний нагруженной платформы J, m=m0 +mг– масса платформы вместе с грузом.
7. Повторите пункты 4-6 для квадратной пластины.
8. Заполните таблицу 3 расчетных значений.
Таблица 2 - Параметры системы
| Наименование | Значение |
| Радиус платформы | R = 75 мм |
| Радиус верхнего диска | r = 40 мм |
| Длина нити | l= 1,125 м |
| Масса платформы | m0 = 110 г |
| Параметры груза в виде круглой пластины: | |
| Масса | mг= 693 г |
| Радиус | Rг = 50 мм |
| Параметры груза в виде квадратной пластины: | |
| Масса | mг= 674 г |
| Сторона квадрата | а = 95 мм |
Таблица 3 – Результаты измерений
| N опыта | n | t, с | tср, с | Тср, с | m, кг | J, кг×м2 | ||
| Ненагруженная платформа | 110.60 | 111.35 | 2.22 | 0.110 | J0=3.6-4 | |||
| 111.40 | ||||||||
| 112.05 | ||||||||
| Нагруженная платформа (круглая пластина) | 72.57 | 72.42 | 1.49 | 0.6928 | 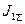 =0.28-4 =0.28-4
| |||
| 71.78 | ||||||||
| 73.32 | ||||||||
| Нагруженная платформа (квадратная пластина) | 82.20 | 82.12 | 1.64 | 0.674 |  =0.26-4 =0.26-4
| |||
| 80.41 | ||||||||
| 83.75 |
9. Вычислите момент инерции первого груза как разницу моментов инерции нагруженной и ненагруженной платформы:  .
.
10. Определите теоретическое значение момента инерции 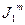 первого груза, представляя его в виде сплошного цилиндра (таблица 1).
первого груза, представляя его в виде сплошного цилиндра (таблица 1).
11. Сравните теоретическое и экспериментальное значения моментов инерции первого груза:  .
.
12. Вычислите момент инерции второго груза как разницу моментов инерции нагруженной и ненагруженной платформы:  .
.
13. Определите теоретическое значение момента инерции 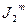 второго груза (таблица 1).
второго груза (таблица 1).
14. Сравните теоретическое и экспериментальное значения моментов инерции второго груза:  .
.
15. Заполните таблицу 4.
Таблица 4 – Моменты инерции тел
| Экспериментальное значение J, кг×м2 | Теоретический момент инерции  , кг×м2 , кг×м2
| δ, % | |
| Круглая пластина | |||
| Квадратная пластина |
6 Контрольные вопросы
1. Что называется моментом инерции вращающейся точки?
2. Момент инерции тела относительно неподвижной оси.
3. Угловая скорость и угловое ускорение.
4. Тангенциальная и нормальная составляющие ускорения.
5. Связь между линейными и угловыми величинами.
6. Решите приведенные ниже тестовые задания.
Задание 1
Диск равнозамедленно вращается вокруг оси как показано на рисунке. Укажите направление вектора тангенциального ускорения точки А на ободе диска.
| 
|
Задание 2
Материальная точка М движется по окружности со скоростью 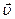 . На рисунке показан график зависимости проекции скорости . На рисунке показан график зависимости проекции скорости 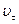 от времени ( от времени (  - единичный вектор положительного направления, - единичный вектор положительного направления, 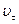 - проекция - проекция 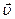 на это направление). При этом для нормального и тангенциального ускорения выполняется условие… на это направление). При этом для нормального и тангенциального ускорения выполняется условие…
| 
| |
o  <0, <0, 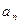 >0
o >0
o  >0, >0, 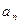 >0 >0
| o  =0, =0, 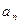 >0
o >0
o  =0, =0, 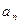 =0 =0
| |
Задание 3
Материальная точка движется по окружности согласно уравнению: 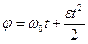 , рад. Здесь , рад. Здесь  , ,  . Чему равна угловая скорость точки через 3 с после начала движения?
(в рад/с) . Чему равна угловая скорость точки через 3 с после начала движения?
(в рад/с)
| |
| o 2 |
|
| o 3 |
|
Задание 4
Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей через его центр. Зависимость проекции угловой скорости от времени показана на графике. Тангенциальные ускорения точек на краю диска в моменты времени t1=2с и t2=7с…
| 
|
Задание 5
Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости 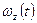 так, как показано на рисунке. Вектор угловой скорости так, как показано на рисунке. Вектор угловой скорости  и вектор углового ускорения и вектор углового ускорения  направлены в одну сторону в интервалы времени… направлены в одну сторону в интервалы времени…
| 
|
Задание 6
Шар и полый цилиндр (трубка), имеющие одинаковые радиусы, скатываются без проскальзывания с горки высотой h. Тогда верным утверждением относительно времени скатывания к основанию горки является следующее:
- быстрее скатится шар
- быстрее скатится полый цилиндр
- оба тела скатятся одновременно
Задание 6
Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости  . Под действием трения стержень остановился, при этом выделилось тепло . Под действием трения стержень остановился, при этом выделилось тепло  . Если стержень раскручен до угловой скорости . Если стержень раскручен до угловой скорости  , то при остановке стержня выделится тепло… , то при остановке стержня выделится тепло…
| 
|
Угловой скоростью  называется векторная величина, равная первой производной угла поворота тела по времени:
называется векторная величина, равная первой производной угла поворота тела по времени:  .
.
Угловым ускорениемe называется векторная величина, равная первой производной угловой скорости по времени:
Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории) и равна 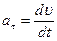 .
.
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории) и равна 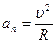
Таким образом, связь между линейными и угловыми величинами выражается следующими формулами:
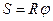 ,
, 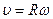 ,
, 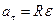 ,
, 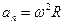 (3)
(3)
В случае равнопеременного движения точки по окружности (e =const)
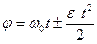 ,
, 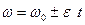 ,
,
где w0 — начальная угловая скорость.
S длина пути
R радиус окружности пройденного точкой по дуге
u линейная скорость
аt тангенциальное ускорение
аn нормальное ускорение
j угол поворота
ω угловая скорость
e угловое ускорение
Моментом инерции J материальной точки массой m относительно оси вращения называется величина, равная произведению массы точки на квадрат расстояния её до рассматриваемой оси:
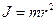 .
.



