 |
|
Обобщенный ряд Фурье
Произвольный сигнал s(t) может быть представлен рядом 
где Cn – коэффициенты, зависящие от вида s(t), а un – n-я функция выбранного базиса 
, причем базисные функции на интервале ортогональности должны обладать свойствами:
а) ортогональности 
, при 
, [a,b] – интервал ортогональности.
б) конечности энергии: 
. Величина этой энергии называется квадратом нормы:
.
Коэффициенты обобщенного ряда Фурье определяются по формуле:
.
Если набор базисных функций содержит комплексные функции, то свойства отображаются таким образом: 
- для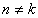 
; здесь 
- функция, комплексно сопряженная uk(t); 
, а комплексные коэффициенты ряда определяются соотношением:
.
Гармонический анализ периодических сигналов
При разложении периодического сигнала s(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут
или
Интервал ортогональности определяется нормой функции 
— среднее значение функции за период.
— основная формула для определения ряда Фурье
Модуль — четная функция, фаза — нечетная функция.
Тогда
Рассмотрим пару для к-го члена
— разложение ряда Фурье
Гармонический анализ непериодических сигналов
Пусть сигнал s(t) задан в виде некоторой функции, отличной от нуля в промежутке (t1,t2). Этот сигнал должен быть интегрируем.
Возьмем бесконечный отрезок времени Т, включающий в себя промежуток (t1,t2). Тогда 
. Спектр непериодического сигнала является сплошным. Заданный сигнал можно представить в виде ряда Фурье 
, где
На основании этого получим: 
Поскольку Т®µ, то сумму можно заменить интегрированием, а W1 на dW и nW1 на W. Таким образом мы прейдем к двойному интегралу Фурье
,
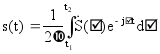где — спектральная плотность сигнала. Когда интервал (t1,t2) не уточнен интеграл имеет бесконечные пределы. Это есть обратное и прямое преобразование Фурье, соответственно.
Если сравнить выражения для огибающей сплошного спектра (модуль спектральной плотности) непериодического сигнала и огибающей линейчатого спектра периодического сигнала, то будет видно, что они совпадают по форме, но отличаются масштабом 
.
Следовательно, спектральная плотность S(W) обладает всеми основными свойствами комплексного ряда Фурье. Т. е. можно записать 
, где
, а 
.
Модуль спектральной плотности 
является нечетной функцией и его можно рассматривать как амплитудно-частотную характеристику. Аргумент 
— нечетная функция рассматриваемая как фазо-частотная характеристика.
На основании этого сигнал можно выразить следующим образом
Из четности модуля и нечетности фазы следует, что подынтегральная функция в первом случая является четной, а во втором — нечетной относительно W. следовательно второй интеграл равен нулю (нечетная функция в четных пределах) и окончательно 
Отметим, что при W=0 выражение для спектральной плотности равно площади под кривой s(t)
.
| Комплексная форма рядов Фурье |
Пусть функция f (x) определена в интервале [−π, π].
Применяя формулы Эйлера
можно записать ряд Фурье данной функции в комплексной форме:
Мы использовали здесь следующие обозначения:
Коэффициенты cn называются комплексными
коэффициентами Фурье. Они определяются формулами
Если нужно построить продолжение функции f (x),
имеюшей произвольный период 2L, то соответствующее
выражение в комплексной форме имеет вид:
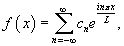где
Комплексная форма ряда Фурье алгебраически
проще и более симметрична. Поэтому, она часто
используется в физике и прикладных расчетах.
|