 |
|
Длина медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого углаBCA и делящий гипотенузу c, пополам. Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
 M - медиана
M - медиана
R - радиус описанной окружности
O - центр описанной окружности
с - гипотенуза
a,b - катеты
α - острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):
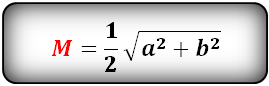
Формула длины через катет и острый угол, (M):

Найти длину медианы треугольника по формулам
Медиана - отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам. Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M - медиана, отрезок |AO|
c - сторона на которую ложится медиана
a , b - стороны треугольника
γ - угол CAB
Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Найти медиану=биссектрису=высоту равностороннего треугольника
Формула для вычисления высоты= биссектрисы= медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
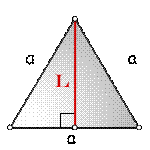
L - высота=биссектриса=медиана
a - стороны треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Длина биссектрисы равнобедренного треугольника
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.

L - высота=биссектриса=медиана
a - одинаковые стороны треугольника
b - основание
α - равные углы при основании
β - угол вершины
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):



Формула высоты, биссектрисы и медианы, через стороны, (L):
