Главная | Обратная связь

Знакопереміжні ряди. Ознака Лейбніца

Нехай задана послідовність додатних чисел

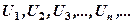, де

Ряд вигляду

(1)

називається знакопереміжним. Умови збіжності знакопереміжних рядів визначаються ознакою Лейбніца.

Теорема (Лейбніца). Нехай члени знакопереміжного ряду (1) монотонно спадають

,

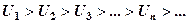тоді ряд буде збіжним, якщо границя його загального члена дорівнює нулю, тобто

.

Доведення. Розглянемо спочатку часткову суму парної кількості доданків

,

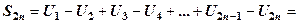
бо кожна дужка додатна за умовою теореми, крім того сума монотонно зростає.

Перепишемо в іншій формі

.

Тут теж кожна з різниць в дужках додатна, тому коли відкинути всі від’ємники, то отримаємо нерівність

.

Оскільки послідовність монотонно зростає і обмежена зверху, то вона має границю, тобто існує

,

Крім того .

Покажемо, що і непарні суми мають ту ж границю:

Отже ряд збігаються і при цьому .

Виділимо в ряді (1) часткову суму 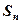, а решту ряду назвемо залишком, позначимо

Таким чином,

. (2)

Залишок теж є збіжним рядом, тому згідно доведеної теореми

Із формули (2) отримуємо

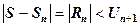
Отже, абсолютна похибка при наближенні суми знакопереміжного ряду частковою сумою 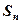не перевищує першого члена , з тих, що відкидаються в ряді (1), коли ряд замінюємо сумою .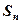

Приклад. Довести збіжність ряду

,

а також обчислити його суму з точністю до 0,1.

Розв’язок. Поскільки , то ряд збіжний. Далі, за умовою , а це буде виконуватися при 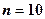, тобто 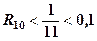. Значить

.

Приклади.

Дослідити на збіжність знакопереміжні ряди, користуючись ознакою Лейбніца.

1. .	2. .	3. .
4. 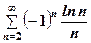.	5. .	6. .
7. .

Відповіді: 1. Збіжний. 2. Збіжний. 3. Розбіжний. 4. Збіжний.

5. Збіжний. 6. Розбіжний. 7. Збіжний.

Знакозмінні ряди. Абсолютна і умовна збіжність

 

Ряд

, (1)

серед членів якого можуть бути як додатні так і від’ємні називаються знакозамінним.

Оскільки ми вже досліджували збіжність додатних рядів, то розглянемо новий ряд із абсолютних величин ряду (1)

(2)

Теорема. Із збіжності ряду (2) випливає збіжність ряду (1).

Якщо збігається ряд (2), то про початковий ряд (1) говорять, що він абсолютно збіжний.

Якщо ж ряд (1) збіжний, а ряд (2) розбіжний, то про ряд (1) говорять, що він умовно збіжний, тобто збіжний за умови, що він містить, як додатні члени, так і від’ємні.

Сформульовану теорему можна виразити ще так: ізабсолютною збіжності випливає умовна збіжність. Обернене твердження в загальному не має місця.

Приклад 1. Ряд - збіжний за ознакою Лейбніца, але ряд із абсолютних величин є гармонічним рядом, розбіжним. Тому початковий ряд є збіжним умовно.

Приклад 2. Ряд , де - задане, є абсолютно збіжним, бо

,

а ряд 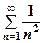, як ми раніше встановили, є збіжним.

Приклади. Встановити, які з рядів збігаються абсолютно, які умовно, які розбігаються.

1. 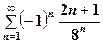.	2. .
3. .	4.
5. .	7. .
6. .

 

Відповіді: 1. Збігається абсолютно. 2. Збігається абсолютно.

3. Збігається умовно. 4. Збігається абсолютно.

5. Збігається абсолютно. 6. Розбігається. 7. Розбігається.

 

Степеневі ряди