Главная | Обратная связь

Деякі властивості, пов’язані з визначеними інегралами

V. Ряди Фур’є

Спочатку нагадаємо означення періодичності функції:

Означення. Функція називається періодичною, якщо існує таке число , від додавання (або віднімання) якого до значення функції не зміниться:

.

Найменше додатне число, яке має таку властивість, називається періодомі позначається буквою :

.

Із означення випливає, що графік періодичної функції повторюється через кожний проміжок довжини (див. рис. 1).

Рис. 1.

Відмітимо властивість визначеного інтеграла, яка пов’язана з періодичністю функції.

Теорема 1. Для всякої періодичної функції періода виконується рівність

, (1)

де - довільне число.

Для доведення використаємо властивість адитивності визначеного інтеграла:

. (2)

В третьому інтегралі зробимо заміну , ,

якщо , то , якщо , то . Отже,

.

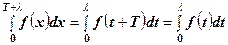Таким чином, останній доданок в правій частині (2) знищується з першим доданком, і тому справджується рівність (1).

Теорема 2. Нехай функція задана на відрізку і є парною , тоді

. (3)

Для доведення необхідно розглянути рівність

,

і в першому інтегралі зробити заміну .

Теорема 3. Нехай функція задана на відрізку і є непарною , тоді

. (4)

5. 2. Ряди Фур’є для періодичних функцій

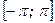Тригонометричний ряд для функції , заданій на відрізку , вигляду

(5)

називається рядом Фур’є, якщо його коефіцієнти, які називаються коефіцієнтами Фур’є для , обчислюються за формулами:

, (6)

, (7)

, (8)

де .

Якщо є - періодичною, то згідно з теоремою 1 із 5.1 у формулах (6)-(8) інтеграли можна брати у межах від 0 до . Вибір відповідних меж залежить від зручності інтегрування.

Умови, яким повинна задовольняти функція , щоб її ряд Фур‘є (5) був збіжним, визначаються відомою теоремою Діріхле.

Теорема(Діріхле). Якщо функція , задана на відрізку 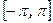задовольняє такі умови:

1) неперервна за винятком скінченого числа точок розриву I роду;

2) має скінчене число екстремумів, то ряд Фур’є функції є збіжним на всьому відрізку 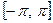, а сума цього ряду:

а) дорівнвє у всіх точках неперервності функції, які лежать усередині інтервала ;

б) дорівнює у всіх точках розриву;

в) дорівнює на кінцях проміжка.

Оскільки членами ряду (5) - - періодичні функції, то із збіжності ряду на відрізку 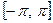випливає його збіжність для всіх . Отже, сума ряду є -періодичною функцією. Таким чином, для збіжності ряду Фур’є саме до функції необхідно вважати, що теж -періодична.

 

5. 3. Ряди Фур’є для парних і непарних -періодичних функцій

Якщо функція - -періодична і парна , то згідно з теоремою 2 із 5.1 формули (6) - (8) спрощуються, а саме,

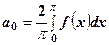, (9)

, (10)

,

де .

Ряд Фур’є для парної функції буде таким:

. (11).

Якщо ж функція - непарна , то відповідно до теореми 3 із 5.1

, (12)

і функція розкладається в ряд Фур’є по синусах:

. (13)

Приклад. Розкласти в ряд Фур’є функцію, яка на проміжку задається рівняння , і далі періодично поширена на всю вісь (див. рис. 2)

 

 

Рис. 2.

Розв’язання. Тут функція - непарна, тому за формулами (12) ,

.

Відповідно до формули (13) маємо:

.

Цей ряд збіжний до у всіх точках проміжка . Зокрема, якщо , то

.

Отже, за допомогою рядів Фур’є можна знаходити суми деяких числових рядів.

 

5. 4. Ряди Фур’є для -періодичних функцій

Якщо функція має період , тобто , то її ряд Фур’є має вигляд:

, (14)

де коефіцієнти Фур’є обчислюються за формулами:

, (15)

, (16)

, (17)

де .

У випадку парності отримаємо розклад по косинусах, тобто

, (18)

причому

(19)

 

, (20)

.

Якщо ж - непарна, то її ряд Фур’є містить синуси, тобто

, (21)

 

де , (22)

.

Зауважимо, що при , то всі формули (14) – (22) збігаються з формулами (5) – (13).

 

Приклад. Розкласти в ряд Фур’є періодичну функцію з періодом , яка на відрізку задається рівнянням

Розв’язання. Дана функція – парна (див. рис 3). Тому за формулою (19) маємо

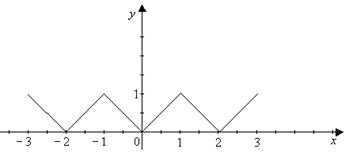Рис. 3.

.

Далі за формулою (20) знаходимо

Для парних , для -непарних , тобто

.

Отже,

.

Оскільки - неперервна для всіх , то ряд Фур’є збігається до для всякого .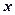

Зокрема, якщо , то отримаємо рівність

.

Звідси знаходимо суму числового ряду

.