Главная | Обратная связь

П.2 Общие свойства сходящихся рядов

Глава V: Числовые ряды

П. 1Определения и примеры

Нам уже приходилось сталкиваться с суммами, содержащими бесконечное число слагаемых. Например, бесконечные десятичные периодические дроби

,

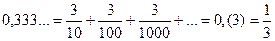бесконечно убывающая геометрическая прогрессия

.

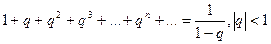Многие числа могут быть записаны в виде таких сумм, с помощью которых их приближенное значение вычисляется с нужной точностью.

Например,

,

,

,

.

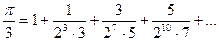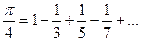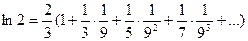Определение 1

Пусть - числовая последовательность. Тогда выражение вида 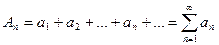называют числовым рядом. При этом называют общим членом ряда .

Замечание 1

Что понимать под суммой бесконечного числа слагаемых? Единого правила нет. Наиболее употребительна интерпретация Коши или суммирование по Коши

Определение 2

Конечная сумма 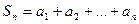первых членов ряда называется n-ой частичной суммой данного ряда.

Заметим, что изучение числовых рядов есть новая форма изучения числовых последовательностей, так как:

1) каждому данному ряду однозначно соответствует последовательность частичных сумм ;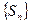

2) каждой данной последовательности 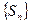однозначно соответствует ряд, для которого эта последовательность является последовательностью его частичных сумм (достаточно положить 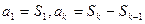при ).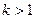

Определение 3:

Говорят, что ряд сходится, если сходится последовательность 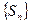его частичных сумм. Тогда число , если существует этот предел, называется суммой ряда .В противном случае, когда предел 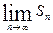не существует или последовательность 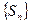является неограниченной, говорят, что ряд расходится.

Пример 1

Рассмотрим ряд:

.

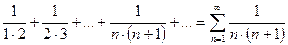Учитывая, что ,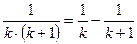

получим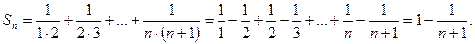

Тогда . Это означает, что исходный ряд сходится, и его сумма равна .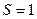

Пример 2

Рассмотрим ряд, составленный из членов геометрической прогрессии:

.

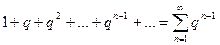Его частичная сумма при 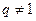имеет вид:

.

Очевидно, что при 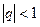последовательность 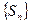сходится и имеет предел, равный . Тогда ряд сходится и имеет сумму 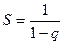. При последовательность 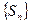неограниченна, следовательно, исходный ряд расходится.

Пример 3

Рассмотрим ряд: 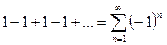. Поскольку последовательность его частичных сумм 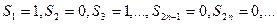не имеет предела, то ряд расходится.

Так как вопрос о сходимости ряда по определению эквивалентен вопросу о сходимости последовательности его частичных сумм, то необходимое и достаточное условие сходимости данного ряда вытекает из критерия Коши сходимости последовательности частичных сумм этого ряда (принцип согласованности).

Теорема 1 Критерий Коши

Для того, чтобы ряд сходился, необходимо и достаточно, чтобы:

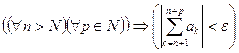, т.е. сколь угодно длинные куски сходящегося ряда могут быть сколь угодно малыми по модулю, если их взять достаточно далеко.

Доказательство:

Для доказательства этой теоремы достаточно заметить, что 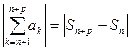и воспользоваться принципом согласованности.

Следствие 1 Необходимый признак сходимости ряда

Если ряд сходится, то .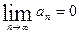

Доказательство:

Пусть ряд сходится. Тогда в силу критерия Коши .

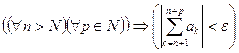Положим . Тогда . Если , то ( ( )) .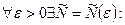

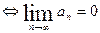Замечание 2

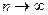Обратное утверждение, вообще говоря, неверно. Стремление к нулю -го члена ряда при является лишь необходимым условием сходимости ряда, т.е. это означает, что если при 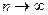не стремится к нулю, то ряд расходится.

 

Пример 4:

Рассмотрим ряд: 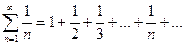, который называют гармоническим. Очевидно, что выполнено необходимое условие сходимости - . Покажем, что ряд сходится. Для этого воспользуемся критерием Коши. Докажем, что для 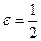не существует такого номера 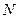, что при для любого натурального выполняется условие .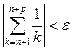

В самом деле, если взять 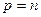, то для сколь угодно большого 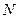: 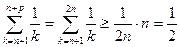. В силу критерия Коши ряд расходится.

 

п.2 Общие свойства сходящихся рядов

Определение 1

Любой ряд 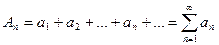можно представить в ви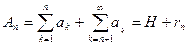де , где - главная часть ряда (голова), а - -й остаток ряда (хвост).

 

Теорема 1

Ряд ведет себя так же, как ведет себя его остаток.

 

Доказательство:

Пусть ряд сходится, т.е. . Тогда 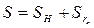, где 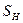- конечная сумма первых членов ряда. Переходя к пределу при фиксированном и , получим, что если ряд сходится, то и значение должно быть конечно, т.е. ряд сходится, и наоборот, если сходится, то значение 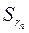конечное, т.е. и 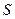конечное, т.е. ряд сходится. Если же значение 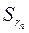не существует или ограниченно, то и должно быть таким же.

 

Теорема 2 Ассоциативность

Пусть ряд сходится. Тогда, не нарушая порядка следования его членов, их можно сгруппировать (произвольным образом расставить скобки) так, что ряд, составленный из групп, будет сходиться к той же сумме, что и исходный ряд.

 

Доказательство:

Сгруппируем члены ряда следующим образом

,

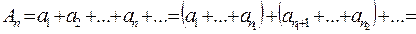
где , …. Составим последовательность частичных сумм , , 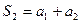…, , , 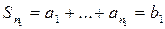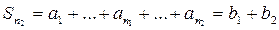…, которая является подпоследовательностью последовательности частичных сумм ряда .

Следует заметить, что для исследования числовых рядов на сходимость достаточно результатов теории числовых последовательностей. Однако эти методы громоздки и чрезвычайно неудобны. Поэтому изучим другие методы исследования сходимости числовых рядов. Для этого удобно рассмотреть отдельно знакопостоянные и знакопеременные ряды. Все признаки сходимости числовых рядов подразделяются на внутренние, когда для решения вопроса о сходимости не привлекаются другие ряды, и внешние, когда поведение исследуемого ряда сравнивается с поведением некоторого эталонного ряда. Рассмотрим их последовательно.