 |
|
П. 3 Ряды с положительными членами
Теорема 1 Критерий Больцано
Для того чтобы ряд 
сходился, необходимо и достаточно, чтобы последовательность 
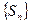его частичных сумм являлась сходящейся.
Доказательство:
Необходимость.
Пусть ряд сходится. Тогда по определению существует предел 
, т.е. последовательность 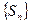является сходящейся. Следовательно, она ограничена.
Достаточность.
Пусть последовательность 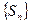ограничена. Так как 
, то последовательность 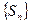монотонно возрастает. Тогда существует предел . Следовательно, ряд сходится.
Пример 1
Рассмотрим ряд: 
.
Тогда 
.
Заметим, что 
,
, … .
Таким образом, 
. Так как правая часть неравенства является суммой бесконечно убывающей геометрической прогрессии с 
, 
, то 
, т.е. последовательность 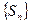ограничена. Тогда по критерию Больцано ряд сходится.
Определение 1
Пусть и 
- ряды с положительными членами. Если найдется номер 
такой, что 
, то ряд называют мажорантойряда , а ряд называют минорантойряда .
Теорема 2 Теорема о мажоранте
Пусть ряд является мажорантойряда . Тогда:
1) если ряд сходится, то сходится и ряд ;
2) если ряд расходится, то расходится и ряд .
Доказательство:
1. Пусть ряд сходится. Так как, начиная с некоторого номера , выполняется неравенст-
во: , то 
. По условию ряд 
сходится. Следовательно, последовательность 
его частичных сумм ограничена. Тогда ограниченной будет последовательность 
частичных сумм ряда 
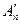, что означает его сходимость. Значит, сходится и ряд .
2. Пусть ряд расходится. Предположим противное, т.е. ряд сходится. Тогда из пункта 1 данной теоремы следует, что ряд сходится. Получили противоречие.
Следствие 2
Пусть и - ряды с положительными членами. Тогда, если существует конечный предел 
, то ряды сходятся или расходятся одновременно.
Доказательство:
Пусть существует конечный предел . Тогда найдется такой номер , начиная с которого выполняется неравенство 
, или 
. По теореме 5 из правой части неравенства и сходимости ряда следует сходимость ряда . Если же ряд расходится, то из левой части неравенства по теореме 5 следует расходимость ряда .
Пример 2
Рассмотрим ряд 
. Так как для любого 
выполняется неравенство 
, и ряд 
расходится 
, то исходный ряд по теореме 2 расходится.
Пример 3
Рассмотрим ряд 
. Так как ряд 
сходится 
, и 
, то по следствию из теоремы 2 исходный ряд сходится.
Теорема 3 Признак Даламбера
Пусть ряд с положительными членами. Тогда:
а) если 
, то ряд сходится;
б) если 
, то ряд сходится при 
и расходится при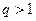 
.
Доказательство:
Пусть 
. Представим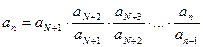 
. Тогда 
, . Так как ряд 
сходится, то сходится ряд (в силу теоремы 5 о мажоранте). Если 
, то 
. Так как 
, то ряд расходится, следующий член ряда не стремится к нулю. Пусть . Тогда найдется номер 
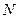, начиная с которого 
или 
. Если , то 
. Тогда в силу теоремы 5 о мажоранте ряд сходится. Если же 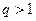, то 
. Тогда в силу той же теоремы ряд расходится.
Замечание 1
Важно, что 
. Например, для гармонического ряда 
, но ряд расходится, так как величина 
не является константой.
Пример 3
Рассмотрим ряд 
. Тогда
.
По признаку Даламбера исходный ряд расходится.
Пример 4
Рассмотрим ряд 
. Тогда 
. По признаку Даламбера исходный ряд сходится.
Теорема 4 Радикальный Признак Коши
Пусть ряд с положительными членами. Тогда:
а) если 
, то ряд сходится;
б) если 
, то ряд сходится при и расходится при .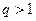
Доказательство:
Пусть 
. Тогда 
. Так как , то ряд 
сходится (это БУГП), то сходится ряд .
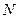Пусть . Тогда найдется номер , начиная с которого 
или 
.
Если , то 
, и ряд 
сходится. Тогда в силу теоремы о мажоранте сходится ряд .
Если 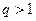, то 
. Тогда в силу теоремы о мажоранте расходится ряд .
Пример 5
Рассмотрим ряд: 
. Тогда 
.
По признаку Коши ряд сходится.
Пример 6:
Рассмотрим ряд: 
.
Тогда 
.
По признаку Коши ряд расходится.
Теорема 5 Теорема Дирихле
Если ряд сходится, то ряд , полученный из ряда перестановкой его членов (заново перенумерованный), тоже сходится и имеет ту же сумму.
Доказательство:
Пусть 
- 
-я частичная сумма ряда . Ее члены находятся в ряде под некоторыми номерами 
. Пусть 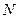- наибольшее число среди них и 
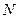- -я частичная сумма ряда . Очевидно, что 
, ( 
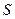- сумма ряда ) и так как произвольно, то ряд сходится и имеет сумму 
.
Теперь приведенные рассуждения можно провести еще раз, поменяв ряды и местами, и получить, что 
. Поэтому 
. ■
Замечание 1
Теперь можно составить алгоритм исследования знакопостоянного ряда на сходимость.