 |
|
п. 4 Знакопеременные ряды
Определение 1
Ряд 
называется знакопеременным, если каждый его член имеет произвольный знак.
Определение 2
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд 
, составленный из модулей его членов.
Определение 3
Ряд называют условно сходящимся, если сам ряд сходится, а ряд 
, составленный из модулей его членов, расходится.
Теорема 1
Если ряд сходится абсолютно, то он сходится.
Доказательство:
Пусть ряд сходится абсолютно. Тогда сходится ряд 
. Отсюда имеем, что ряд 
тоже сходится. Рассмотрим ряд 
. Заметим, что 
. Следовательно, по теореме о мажоранте ряд 
сходится. Но ряд 
. Значит, что сходится и ряд . ■
Теорема 2 Теорема Римана
Пусть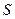 
- некоторое число 
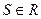и ряд 
- сходится условно. Тогда члены ряда можно представить так, что его сумма равна .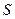
Доказательство:
Для доказательства теоремы используем следующую лемму.
Лемма
Пусть ряд является условно сходящимся. Тогда его можно представить в виде суммы двух рядов 
, где - ряд с неотрицательными членами, а 
- ряд с отрицательными членами, причем оба ряда расходятся.
{*Пусть . Рассмотрим ряд 
. По условию ряд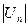 
- расходится, тогда хотя бы один из рядов ( или ) должен расходиться.
*}.
Пусть число 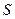- для определенности неотрицательное 
. По лемме его ( ) можно записать в виде: , где - ряд, составленный из неотрицательных членов ряда, а - ряд, составленный из отрицательных членов ряда.
По лемме ряды и - расходятся. Выберем из ряда подряд столько членов, чтобы их сумма превышала 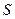и чтобы меньшее число таких членов не превышало 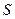, т.е. выберем число 
такое, что:
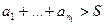
. Это можно сделать, так как ряд - расходится, т.е.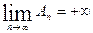 
.
Выберем число 
таким, что 
, 
. Это можно сделать, так как ряд - расходится, т.е. 
.
Выберем число 
таким, что 
, 
.
Выберем число 
таким, что … и т. д. Получим ряд: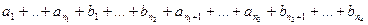 
.
Рассмотрим последовательность его частичных сумм: 
, 
, 
, …, 
, … 
, 
, … Причем отклонение от числа 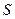каждой из частичных сумм не превышает ее последнего члена по модулю, т.е. можно записать следующее неравенство 
. По условию ряд сходится, т.е. его общий член стремится к нулю, а это значит, что 
. Если взять любую частичную сумму 
ряда , то всегда можно найти такой номер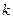 
, зависящий от 
, что 
, 
. По теореме о двух милиционерах получаем, что 
.
Пример 1
Рассмотрим ряд 
: 
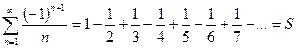. Сумму этого ряда можно ограничить так: 
.
,
, 
.
П. 5 Ряды Лейбница
Определение 1
Знакопеременный ряд вида 
, где 
- положительные члены ряда, называется знакочередующимся рядом.
Теорема 1 Признак Лейбница
Пусть знакопеременный ряд такой, что:
1) 
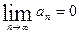(убывание);
2) 
(монотонность).
Тогда ряд сходится (условно или абсолютно).
Доказательство:
Рассмотрим знакочередующийся ряд : 
. Тогда последовательно-
сть его частичных сумм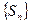 
такова, что 
. Так как по условию 2: 
, 
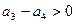, …, то последовательность 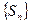монотонно возрастает. С другой стороны, 
. По условию 2 
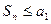, т.е. последовательность 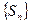ограничена сверху. Тогда существует предел частичных сумм ряда , что означает его сходимость. ■
Пример 1
Рассмотрим ряд: .
Проверим, выполняются ли условия теоремы Лейбница:
1) 
;
2) 
.
Тогда по признаку Лейбница исходный ряд сходится. Но ряд, составленный из модулей его членов, 
расходится. Значит, исходный ряд сходится условно.
Пример 2
Рассмотрим ряд: 
.
Заметим, что нарушается условие монотонности: 
. Значит, ряд расходится.
Следует отметить, что исходный ряд можно представить следующим образом: 
, причем ряд, заключенный в первой скобке, расходится, а во второй - сходится.
Следствие 1
Сумма остатка знакочередующегося ряда по модулю меньше его первого члена: 
.
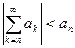Замечание 1
Данное следствие позволяет находить сумму знакочередующегося ряда с любой заданной точностью.