Главная | Обратная связь

Если выполнены оба условия, то ряд сходится.

Краткая справка о модуле приведена в методичке Горячие формулы школьного курса математики, но для удобства ещё раз:

Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду . Мысленно сотрём ластиком все знаки ипосмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначает одно и то же:

– Члены ряда без учёта знака убывают.
– Члены ряда убывают по модулю.
– Члены ряда убывают по абсолютной величине.
– Модуль общего члена ряда стремится к нулю: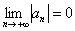

Конец справки

Теперь немного поговорим про монотонность. Монотонность – это скучное постоянство.

Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член рядапо модулю МЕНЬШЕ, чем предыдущий: . Для ряда выполнена строгая монотонность убывания, её можно расписать подробно:

А можно сказать короче: каждый следующий член ряда по модулю меньше, чем предыдущий: .

Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: . Рассмотрим ряд с факториалом: Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего: .

В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). При этом члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим.

Не нужно пугаться того, что я нагородил, практические примеры всё расставят по своим местам:

Пример 1

Исследовать ряд на сходимость

В общий член ряда входит множитель 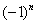, а значит, нужно использовать признак Лейбница

1) Проверка ряда на знакочередование. Обычно в этом пункте решения ряд расписывают подробно и выносят вердикт «Ряд является знакочередующимся».

2) Убывают ли члены ряда по модулю? Необходимо решить предел , который чаще всего является очень простым.

– члены ряда не убывают по модулю. К слову, отпала надобность в рассуждениях о монотонности убывания.

Вывод: ряд расходится.

Как разобраться, чему равно 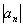? Очень просто. Как известно, модуль уничтожает минусы, поэтому для того, чтобы составить , нужно просто убрать с крыши проблесковый маячок. В данном случае общий член ряда . Тупо убираем «мигалку»: .

Пример 2

Исследовать ряд на сходимость

Используем признак Лейбница:

1)
Ряд является знакочередующимся.

2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: , таким образом, убывание монотонно.

Вывод: ряд сходится.

Всё бы было очень просто – но это еще не конец решения!

Если ряд сходится по признаку Лейбница, то также говорят, что ряд сходится условно.

Если сходится и ряд, составленный из модулей: 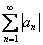, то говорят, что ряд сходится абсолютно.

Поэтому на повестке дня второй этапрешения типового задания – исследование знакочередующегося ряда на абсолютную сходимость.

Не виноватый я – такая уж теория числовых рядов =)

Исследуем наш ряд на абсолютную сходимость.
Составим ряд из модулей – опять просто убираем множитель, который обеспечивает знакочередование:
– расходится (гармонический ряд).

Таким образом, наш ряд не является абсолютно сходящимся.
Исследуемый ряд сходится только условно.

Заметьте, что в Примере №1 не нужно проводить исследование на абсолютную сходимость, поскольку еще на первом шаге сделан вывод о том, что ряд расходится.

Собираем ведёрки, лопатки, машинки и выходим из песочницы, чтобы смотреть на мир широко открытыми глазами из кабины моего экскаватора:

Пример 3

Исследовать ряд на сходимость

Используем признак Лейбница:

1)
Данный ряд является знакочередующимся.

2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: , значит, убывание монотонно.

Вывод: Ряд сходится.

Исследуем ряд на абсолютную сходимость:

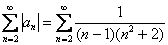
Анализируя начинку ряда, приходим к выводу, что здесь нужно использовать предельный признак сравнения. Скобки в знаменателе удобнее раскрыть:

Сравним данный ряд со сходящимся рядом . Используем предельный признак сравнения.

Получено конечное число, отличное от нуля, значит, ряд сходится вместе с рядом .

Исследуемый ряд сходится абсолютно.

Готово.

Пример 4

Исследовать ряд на сходимость

Пример 5

Исследовать ряд на сходимость

Это примеры для самостоятельного решения. Полное решение и образец оформления в конце урока.

Как видите, знакочередующиеся ряды – это просто и занудно! Но не спешите закрывать страницу, всего через пару экранов мы рассмотрим случай, который многих ставит в тупик. А пока еще пара примеров для тренировки и повторения.

Пример 6

Исследовать ряд на сходимость

Используем признак Лейбница.
1) Ряд является знакочередующимся.
2)

Члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.

Вывод: ряд сходится.

Обратите внимание, что я не расписал подробно члены ряда. Их всегда желательно расписывать, но от непреодолимой лени в «тяжелых» случаях можно ограничиться фразой «Ряд является знакочередующимся». Кстати, не нужно относиться к этому пункту формально,всегда проверяем (хотя бы мысленно) что ряд действительно знакочередуется. Беглый взгляд подводит, и ошибка допускается «на автомате». Помните об «обманках» 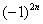, , 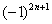, 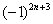если они есть, то от них нужно избавиться, получив «обычный» ряд с положительными членами.

Вторая тонкость касается фразы про монотонность, её я тоже максимально сократил. Так делать можно, и почти всегда вашу задачу зачтут. Скажу совсем нехорошую вещь – лично я часто вообще умалчиваю о монотонности, и такой номер проходит. Но будьте готовы всё расписать детально, вплоть до подробных цепочек неравенств (см. пример в начале урока). Кроме того, иногда монотонность бывает нестрогой, и за этим тоже нужно следить, чтобы заменить слово «меньше» на слово «не больше».

Исследуем ряд на абсолютную сходимость:

Очевидно, что нужно использовать радикальный признак Коши:

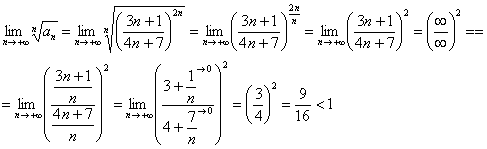
Таким образом, ряд сходится.

Исследуемый ряд сходится абсолютно.

Пример 7

Исследовать ряд на сходимость

Это пример для самостоятельного решения. Хммм… что-то я немного погорячился на счет простоты.

Нередко встречаются знакочередующиеся ряды, которые вызывают затруднения.

Пример 8

Исследовать ряд на сходимость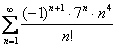

Используем признак Лейбница:
1) Ряд является знакочередующимся.

2)

Дело в том, что не существует стандартных обыденных приемов для решения подобных пределов. Куда стремится такой предел? К нулю, к бесконечности? Здесь важно, ЧТО на бесконечности растёт быстрее – числитель или знаменатель.

Примечание: понятие порядка роста функции подробно освещено в статье Методы решения пределов. У нас пределы последовательностей, но это не меняет сути.

Если числитель при растёт быстрее факториала, то . Если, на бесконечности факториал растёт быстрее числителя, то он, наоборот – «утянет» предел на ноль: . А может быть этот предел равен какому-нибудь отличному от нуля числу?

Попробуем записать несколько первых членов ряда:

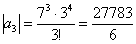
Создается стойкое впечатление, что , но где гарантия, что при очень больших «эн» факториал не «обгонит» числитель и не утащит предел на ноль?

Обратимся к теории математического анализа, для того она и существует:

Справка

– Факториал растёт быстрее, чем любая показательная последовательность, иными словами: или . Да хоть миллион в степени «эн», это не меняет дела. То есть, факториал более высокого порядка роста, чем любая показательная последовательность.

– Факториал растёт быстрее, чем любая степенная последовательность или многочлен, иными словам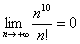и: или . Вместо 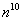можно подставить какой-нибудь многочлен тысячной степени, это опять же не изменит ситуацию – рано или поздно факториал всё равно «перегонит» и такой страшный многочлен. Факториал более высокого порядка роста, чем любая степенная последовательность.

– Факториал растёт быстрее, чем произведение любого количества показательных и степенных последовательностей (наш случай).

– Любая показательная последовательность растёт быстрее, чем любая степенная последовательность, например: , . Показательная последовательность более высокого порядка роста, чем любая степенная последовательность. Аналогично факториалу, показательная последовательность «перетягивает» произведение любого количества любых степенных последовательностей или многочленов: .

– А есть ли что-нибудь «круче» факториала? Есть! Степенно-показательная последовательность («эн» в степени «эн») растёт быстрее факториала. На практике встречается редко, но информация лишней не будет.

Конец справки

Таким образом, второй пункт исследования (вы еще об этом помните? =)) можно записать так:
2) , так как более высокого порядка роста, чем .
Члены ряда убывают по модулю, начиная с некоторого номера 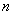, при этом, каждый следующий член ряда по модулю меньше, чем предыдущий, таким образом, убывание монотонно.

Вывод: ряд сходится.

Вот здесь как раз тот любопытный случай, когда члены ряда сначала растут по модулю, из-за чего у нас сложилось ошибочное первоначальное мнение о пределе. Но, начиная с некоторого номера «эн», факториал обгоняется числитель, и «хвост» ряда становится монотонно убывающим, что является принципиально важным для выполнения условия теоремы Лейбница. Чему конкретно равно данное «эн», выяснить достаточно трудно.

Исследуем ряд на абсолютную сходимость:

А тут уже работает старый добрый признак Даламбера:

Используем признак Даламбера:

Таким образом, ряд сходится.

Исследуемый ряд сходится абсолютно.

Разобранный пример можно решить другим способом.