Главная | Обратная связь

Арифметика чисел большой разрядности

 

Размерность обрабатываемых в вычислительных машинах чисел обычно ограничивается размерностью машинного слова. Типичная переменная целочисленного типа занимает в памяти машины 8, 16, 32 или 64 бит. Для многих криптографических алгоритмов требуются числа намного большего размера. Например, рекомендуемый размер открытого ключа для алгоритма RSA составляет 4 Кбит. Рассмотрим реализацию базовых арифметических операций над целыми числами большого размера. Для представления цифр больших чисел удобно использовать систему счисления с основанием b, равным 2^m, где m – размер машинного слова. Это наиболее компактный способ представления больших чисел, позволяющий хранить все цифры в массиве слов-переменных.

Алгоритм сложения

Алгоритм сложения неотрицательных чисел достаточно прост: цифры числа складываются, начиная с младших разрядов к старшим. Если зафиксировано переполнение (т. е. при сложении получена цифра, большая максимально возможной в данной системе счисления), то происходит перенос значения в следующий разряд. Рассмотрим реализацию сложения неотрицательных n‑разрядных целых чисел (u_n‑1, …, u₀)_b и (v_n‑1, …, v₀)_b по основанию b. Следующий алгоритм формирует их сумму (w_n, w_n‑1, …, w₀)_b, причем w_n Î {0, 1}:

ADD(u, v, n)

j := 0; k := 0;

while j < n

do w_j := u_j + v_j + k

if w_j ≥ b

then w_j := w_j – b

k := 1

else k := 0

j := j + 1

w_n := k

return (w_n, …, w₀)

Заметим, что при работе этого алгоритма всегда выполняются соотношения u_j + v_j + k ≤ (b – 1) + (b – 1) + 1 < 2b, так что размер результата суммирования не превышает log₂2b = b + 1 разрядов. Приведенный алгоритм может использоваться и для сложения отрицательных чисел. Для этого следует использовать их представление в дополнительном коде.

Алгоритм умножения

Умножение больших чисел может быть выполнено традиционным школьным способом «в столбик». Однако вместо использования массива промежуточных результатов гораздо эффективнее добавлять к произведению каждую новую строку немедленно после ее вычисления.

Если множимое состоит из m слов, множитель – из n слов, то произведение занимает не более m + n слов, независимо от того, выполняется знаковое или беззнаковое умножение. Рассмотрим реализацию умножения неотрицательных целых чисел (u_m‑1, …, u₀)_b и (v_n‑1, …, v₀)_b по основанию b. Следующий алгоритм формирует их произведение (w_{m + n – 1}, …, w₀)_b:

MULTIPLY (w, v, m, n)

forj = 0, …, m – 1 do w_j := 0;

j := 0;

while j < n

do if v_j > 0

then i := 0; k := 0;

while i < m

do t := u_i ∙ v_j + w_i+j + k:

w_i+j := t mod b;

k := ;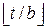

i := i + l;

w_{j + m} := k;

else w_{j + m} := 0;

j := j + l;

return (w_{m + n ‑ 1}, …,w₀)

На каждом шаге алгоритма умножения выполняются неравенства

0 ≤ t < b², 0 ≤ k < b.

Умножение больших чисел выполняется проще для беззнаковых операндов. Знак произведения получается как результат операции «ИСКЛЮЧАЮЩЕЕ-ИЛИ» над разрядами знака множителей.

Умножение целых чисел может быть существенно ускорено. Например, пусть u = bⁿU₁ + U₀, v = bⁿV₁ + V₀. Тогда (алгоритм Карацубы)

uv = b²ⁿU₁V₁ + bⁿ(U₁V₀ + U₀V₁) + U₀V₀ =
= b²ⁿU₁V₁ + bⁿ((U₀ + V₀)(U₁ + V₁) – U₀V₀ – U₁V₁) + U₀V₀ =
= b²ⁿC₀ + bⁿ(С₂ – С₁ – С₀) + С₁, (11)

где С₀ = U₁V₁, С₁ = U₀V₀, С₂ = (U₀ + U₁)(V₀ + V₁).

Алгоритм Карацубы сводит задачу умножения двух чисел к нескольким задачам умножения чисел меньшей разрядности. Разбиение может осуществляться рекурсивно до тех пор, пока разрядность не уменьшится до поддерживаемой аппаратно (т.е. пока n не достигнет размера машинного слова). В этом случае число элементарных умножений для алгоритма Карацубы асимптотически сходится к .

Пример: 13 ∙ 27 = 100 ∙ 1 ∙ 2 + 10 ∙ (3 ∙ 7 + 1 ∙ 2) + 3 ∙ 7 = 100 ∙ 2 + 10 ∙ (36 –
– 21 – 2) + 21 = 200 + 130 + 21 = 351.

Обобщением алгоритма Карацубы является алгоритм Тома–Кука, в котором множители могут разбиваться более чем на две части. Максимальной скоростью на сегодняшний день обладает алгоритм умножения на основе быстрого преобразования Фурье. В этом случае цифры произведения получаются как коэффициенты свертки цифр множителей, посчитанные с учетом переносов значений между коэффициентами.

Деление

Основная сложность при реализации классического метода деления «в столбик» состоит в необходимости угадывать разряды частного на каждой итерации алгоритма. Этот процесс должен быть формализован. Прежде всего заметим, что деление т-разрядного числа на п-разрядное (т > п) сводится к последовательности делений (п + 1)-разрядных чисел и на n-разрядное число v,причем 0 ≤ u/v < b, где b – основание системы счисления. Таким образом, необходимо построить алгоритм для нахождения q = , u = (u_n, u_n‑1, …, u₀)_b и
v = (v_n, v_n‑1, …, v₀)_b.

Условие u/v < b может быть переформулировано как и/b < v,т. е.
(u_n, u_n‑1, …, u₁)_b < v = (v_n, v_n‑1, …, v₀)_b.Частное q должно быть единственным целым числом, таким, что 0 ≤ и – qv < v.Попытаемся угадать q как

(12)

В данном случае 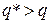, при этом если q* превышает q,то превышение незначительно. Кроме того, если v_n-1 ≥ , то . Это условие носит название условия нормализации. Его можно обеспечить, домножив делимое и делитель на . Дополнительно можно показать, что если , то q* < q,где r* = u_пb + u_n–1 + q*v_n–1. В противном случае
q Î{ q*, q* – 1}.

Исходя из этих соображений, алгоритм вычисления частного m и остатка n от деления (u_m+n‑1, …, u₀)_b на (v_n‑1, …, v₀)_b имеет вид

DIVIDE(u, v, m, n) d := ; (um+n, um+n‑1, …, u0)b := d ∙ (um+n‑1, …, u0)b (vn‑1, …, v0)b := d ∙ (vn‑1, …, v0)b j := m while j ≥ 0 do if then if then (uj+n, …, uj)b := (uj+n, …, uj)b – q*(vn‑1, …, v0)b if (uj+n, …, uj)b < 0 then NegFlag := true (uj+n, …, uj)b := (uj+n, …, uj)b + bn+1 else NegFlag := false qj = q* if NegFlag = true then qj := qj – 1 (uj+n, …, uj)b := (uj+n, …, uj)b + (0, vn‑1, …, v0)b j := j – l return ((qm, …, q1q0)b, (un-1, …, u0)b /d)

Некоторые фрагменты этого алгоритма выполняются очень редко, что затрудняет отладку.

Задания

1. Реализуйте алгоритмы «в столбик» для вычисления суммы, произведения и частного двух целых чисел большой разрядности.

2. Реализуйте алгоритмы Карацубы для умножения целых чисел большой разрядности.

3. Сравните скорость работы и затраты памяти для реализованных в заданиях 1 и 2 алгоритмов умножения целых чисел большой разрядности.