Главная | Обратная связь

Предельная теорема для редеющего потока.

Рассмотрим специфическую операцию «разрежения» потока, когда событие переносится в разреженный поток с вероятностью p и, следовательно, отбрасывается с вероят-ностью . Рис.1.14. поясняет такое разрежение потока, где обозначено: П–исходный поток (стационарный поток Пальма) и П_р – разреженный поток.

Исследуем характеристики потока П_р. Для Т_р справед-ливо: , где случайные величины Т_i взаимно незави-симы, z – случайная величина, представляющая собой число просуммированных интервалов.

Найдем вероятность того, что случайное число z равно некоторому фиксированному k.

Рис.1.14. Вероятностное разрежение потока.

 

Очевидно:

.

Предположим z=k. Тогда при справедливости этой гипотезы характеристическая функция (условная) случайной величины Т_р определяется как:

,

где g(x) - характеристическая функция случайной величины Т_р.

Безусловная характеристическая функция:

.

Результат получен в предположении и с использованием формулы для суммы членов геометрической прогрессии при . (Если - геометрическая прогрессия со знаменателем r , то и ). Зная 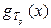всегда можно найти плотность распределения .

Найдём числовые характеристики случайной величины Т_р, но предварительно вычислим и .

.

.

Среднее найдём через характеристическую функ-цию 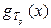. Согласно (1.11):

.

, так как .

Итак . Но , поэтому:

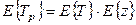. (1.58)

Рассуждая аналогично, можно получить:

. (1.59)

Очевидно, что интенсивность простейшего потока мож-но определить как . Соответственно для разреженного потока с учетом (1.58) запишем

.

Теперь можно перейти к предельной теореме для редеющих потоков. Смысл её состоит в том, что если последовательно разрежать ординарный стационарный поток Пальма достаточно большое число, то такой многократно разрежённый поток будет близок к простейшему.

На практике уже 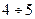кратное разрежение (при р<0,8) даёт поток близкий к простейшему, даже если исходный поток был регулярным.