Главная | Обратная связь

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

 

Асимметричные системы шифрования. Смысл асимметричных криптосистем (системы открытого шифрования, с открытым ключом - publi key systems) состоит в том, что для зашифрования и расшифрования используются разные преобразования. Одно из них - зашифрование - является абсолютно открытым для всех. Другое же - расшифрование - остается секретным за счет секретности ключа расшифрования. Таким образом, любой, кто хочет что-либо зашифровать, пользуется открытым преобразованием, но расшифровать и прочитать это сможет лишь тот, кто владеет секретным ключом. Схема асимметричной криптосистемы представлена на рис. 2.1.

 

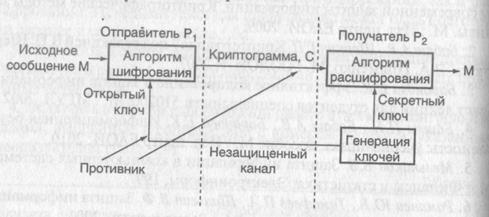
Рис. 2.1. Обобщенная схема асимметричной криптосистемы

 

В настоящее время во многих асимметричных криптосистемах вид преобразования определяется ключом. У пользователя есть два ключа - секретный и открытый. Открытый ключ публикуется в общедоступном месте, и каждый, кто хочет послать сообщение этому пользователю, зашифровывает текст открытым ключом. Расшифровать сообщение может только упомянутый пользователь с секретным ключом. Таким образом, отпадает проблема передачи секретного ключа, как в симметричных системах. Однако, несмотря на все свои преимущества, эти криптосистемы достаточно трудоемки и медлительны. Стойкость асимметричных криптосистем базируется в основном на алгоритмической трудности решить за приемлемое время какую-либо задачу. Если злоумышленнику удастся построить такой алгоритм, то дискредитирована будет вся система и все сообщения, зашифрованные с помощью этой системы. В этом состоит главная опасность асимметричных криптосистем в отличие от симметричных.

Алгоритм Диффи - Хелл.мана. Алгоритм Диффи _ Хеллман (Diffie - Hellman) использует функцию дискретного возведения в степень. Вначале генерируются два больших простых числа n и q. Эти два числа не обязательно хранить в секрете. Далее один из партнеров Р₁ генерирует случайное число х и посылает другому участнику будущих обменов Р₂ значение

А=q^x mod n.

 

По получении значения А партнер Р₂ генерирует случайное число у и посылает участнику обмена Р₁ вычисленное значение

 

B=q^y mod n.

 

Партнер P₁, получив значение В, вычисляет К_x = B^x mod n, а партнер Р2 – К_y = А^y mod n. Алгоритм гарантирует, что числа К_y и К_x равны и могут быть использованы в качестве секретного ключа для шифрования. даже перехватив числа А и В, трудно вычислить К_x или К_y Схематично работа алгоритма Диффи - Хеллмана представлена на рис. 2.2.

 

Рис. 2.2. Алгоритм Диффи - Хеллмана

Пример2.1

n=5,q,=7,x,=3,y,=2

А,= 7³ (mod 5) = 343 (mod 5) = 3; В,= 7² (mod 5) = 49 (mod 5) = 4;

К_x= 7³ (mod 5) = 64 (mod 5) = 4; К_y= 3² (mod 5) = 4.

 

Алгоритм RSA. Первое практическое воплощение принцип открытого шифрования получил в системе RSA, разработанной в 1977 г. в Массачусетском технологическом институте (США) и получившей свое название от первых букв фамилий авторов: Рональд Риве (R. Rivest), Эди Шамир (А. Shamir), Леонард Адлеман (L. Adleman).

Идея авторов этого алгоритма состояла в том, что, взяв целое число N в виде произведения двух больших простых чисел N = Р: Q, легко подобрать пару чисел У и Х, таких, чтобы для любого целого числа М. меньшего N, было справедливо соотношение

 

(М^x)^y = M mod N.

 

В качестве открытого ключа шифрования в системе RSA выступа ключ У и модуль N, а секретным ключом для расшифрования сообщений является число Х Процедура шифрования сообщения М, рассматриваемого как целое число (такое допущение возможно вследствие того, что любой контент может быть представлен в числовой форме пр обработке в средствах вычислительной техники), меньшее N (при необходимости длинное сообщение разбивается на отрезки, шифруемы независимо), состоит в вычислении значения

 

С= M^y mod N.

 

Расшифрование осуществляется аналогично с использование секретного ключа Х

 

M=C^x mod N.

 

Математически строго можно доказать, что определение по паре чисел (N, У) секретного ключа Х не проще разложения на простые множители числа N, т.е. нахождения Р и Q. Задача же разложения на множители целого числа изучается в математике с древнейших времен и известна как сложная вычислительная задача. В настоящее время разложение числа из нескольких сотен десятичных знаков потребует от современных вычислительных машин сотен лет непрерывной работы.

Далее представлен пример работы алгоритма RSA.

Генерация ключей

Получатель 1. Р, Q - простые, N = Р*Q

2. = (Р - 1) * (Q - 1), - функция Эйлера

Выбор открытого ключа У: .

1 < Y ≤ , НОД(У, ) = 1

Выбор открытого ключа X:

Х * Y 1 (mod < )

Отправитель шифрование M(M_i= 0,1,2, ... , N - 1)

3. С_i = М_i^y (mod N)

Получатель расшифрование C(C1, С2, … , C_i, …)

4. M_i = С_i^X (mod N)

 

Пример

Генерация ключей

1.Р=3, Q=11,N=P·* Q=33

2 = (P- 1) . (Q - 1), -1

Y= 7, НОД(У, ) = 1

Х * Y= 1 (mod 20),7 *·3 = 1 (mod 20), Х= 3

Сообщение: M₁M₂ 32; М₁ = 3 < 33, М₂ = 2 < 33

Шифрование С_i = М_i^y (mod N)

3. С₁ = 3⁷ mod 33 = 2187 mod 33 = 9

С² = 2⁷ mod 33 = 128 mod 33 = 29

Расшифрование

M_i = С_i^X (mod N)

4. М₁ = 9³ mod 33 = 729 mod 33 = 3

М₂ = 29³ mod 33 = 24389 mod 33 = 2

 

Методы проверки чисел на простоту. Одна из главных проблем асимметричного шифрования - генерация больших простых чисел. Простейшим методом проверки простоты натурального числа N является метод пробных делений: для d = 2, 3 ... проверяется выполнение условия (d, N) >1 (здесь (d, N) - наибольший общий делитель чисел d, N). Число операций, требуемых для этого метода, имеет порядок . Поэтому уже для чисел порядка 10³⁰-10⁴⁰ этот метод не применим.

В отличие от таких детерминированных методов существуют еще вероятностные методы проверки простоты. для исследуемого числа проверяется выполнение некоторых условий, связанных со случайными числами. Если какое-либо из этих условий не выполнено, то N - составное число. Если же все условия выполнены, то с некоторой вероятностью можно утверждать, что N - простое число. Эта вероятность тем ближе к единице, чем большее количество случайных чисел мы проверим. Обычно эти условия основаны на малой теореме Ферма, Утверждающей, что для любого положительного числа b, не превосходящего некоторого простого числа р,

 

b^(P-1) = l (mod р).

 

Например, 2⁶ = 64 = 63 + 1 = 1 (mod 7). Если требуется определить, является ли целое число r простым, то можно выбрать любое положительное целое число b, меньшее r, и проверить, выполнено ли равенство

 

b^(r-1) = l (mod г).

 

Если равенство не выполнено, то на основании теоремы Ферма можно быть совершенно уверенным, что r - не простое число. Если же равенство выполнено, то можно лишь предполагать, что r - простое число, и поэтому назвать его псевдопростым по основанию b. Вероятность Р(х) того, что составное число х окажется псевдопростым по случайному основанию, убывает с ростом х.

К сожалению, существуют так называемые числа Кармайкла - составные числа, которые обладают свойством

b^(r-1) == l (mod r) для всех b из интервала (1, r], которые взаимно просты с r.

Примером числа Кармайкла является число 561 == 3*11*17.

Классический результат теории чисел - теорема Чебышева - показывает, что доля положительных целых чисел, меньших некоторого целого m и являющихся простыми, близка к l/(ln m). Например, доля целых чисел, меньших 10¹⁰⁰ и являющихся простыми, близка к 1/(ln 10¹⁰⁰) == 1/230. Таким образом, если выбрать случайно большое целое положительное нечетное число х и последовательно Проверять на простоту числа х, х + 1, х + 2, … , то в среднем впервые простое число встретится на шаге с номером ln х.