Главная | Обратная связь

Преобразование Уолша-Адамара

При проведении дифференциального и линейного криптоанализа, а также исследовании корреляционных свойств булевых функций (БФ), описывающих примитивы блочных алгоритмов шифрования основным аппаратом анализа является преобразование Уолша-Адамара – разновидность дискретного преобразования Фурье над конечным полем Галуа. Данное преобразование позволяет непосредственно оценить такие показатели качества БФ, как:

q сбалансированность;

q нелинейность;

q корреляционная иммунность.

Кроме того, с помощью преобразования Уолша-Адамара можно получить оценки автокорреляционных свойств БФ и различных показателей распространения изменений.

Очевидно, что БФ не могут удовлетворять всем показателям одновременно, поэтому возникает задача некоторого компромисса (оптимизации) в выборе БФ, удовлетворяющих тем или иным показателям.

Под преобразованием Уолша-Адамара (ПУА) функции f(X), XÎGF(2)ⁿ, относительно вектора aÎGF(2) понимается линейное преобразование GF(2)ⁿ®Z, принимающее значение в области действительных чисел и имеющее следующий вид:

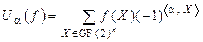(2)

где знак “ ” – обозначает скалярное произведение двух векторов.

Для сопряженной функции , осуществляющей отображение из GF(2)ⁿ в множество {-1, 1}, ПУА преобразуется к следующему виду:

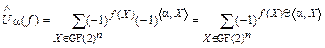. (3)

Обратное преобразование Уолша-Адамара (ОПУА) задается выражениями:

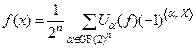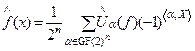, . (4)

Если 2ⁿ значений таблицы истинности S(f) БФ f(X) и 2ⁿ значений действительной функции U_a(f ) записать в виде вектор-столбцов [S(f )] и [U_a(f )], то линейное преобразование Уолша-Адамара задается матрицей Адамара H_n в следующем виде:

[U_a(f )] = H_n[S(f)]. (5)

Аналогично .

Матрица H_n формируется итеративно:

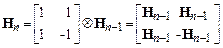, H₀ = [1], (6)

где Ä – означает кронекеровское произведение матриц.

Кронекеровское произведение матрицы A размера m´n и матрицы B размера s´t – это матрица размера ms´nt задаваемая как

, (7)

где a_ij – элемент i-ой строки и j-го столбца матрицы A.

Если записать матрицу Адамара с помощью ее строк h_i

,

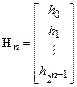то каждая строка h_i матрицы H_n является характеристической последовательностью линейной функции 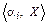, где вектор a_iÎGF(2)ⁿ, а его целочисленное представление равно i. В свою очередь каждая характеристическая последовательность линейной функции от n переменных является строкой матрицы H_n. Откуда следует, что строки матриц H_n и 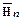, охватывают последовательности всех аффинных функций над GF(2)ⁿ. Здесь 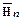- матрица, все элементы которой являются инверсией элементов матрицы H_n.

Обратное ПУА описывается следующими соотношениями:

[S(f)] = 2^-nH_n[U_a(f )], .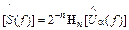

Алгоритм преобразования Уолша-Адамара имеет сложность O(n2ⁿ) операций.