 |
|
Остаток сходящегося ряда. Необходимое условие сходимости. Гармонический ряд
Числовые и степенные ряды
Занятие 1. знакоположительные ряды
Числовые ряды. Сходимость и расходимость
Основными, базовыми понятиями теории рядов являются понятия ряда, частичной суммы, сходимости.
Определение. Пусть задана бесконечная последовательность чисел:
u1, u2, u3,. . . , un, . . .
Выражение u1 + u2 + u3 +. . . + un+…, обозначаемое еще 
, называется бесконечной суммой или числовым рядом, а числа u1, u2, u3,. . . , un, . . . его членами.
Определение. Сумма конечного числа n первых членов ряда называется n-й частичной суммой ряда:
.
Рассмотрим последовательность частичных сумм
Если существует конечный предел этой последовательности:
,
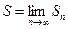то его называют суммой ряда и говорят, что данный ряд сходится, в противном случае – расходится.
В качестве примера числового ряда рассмотрим бесконечную геометрическую прогрессию. Выясним, при каких условиях сходится сумма членов геометрической прогрессии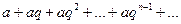 
.
Решение
Сумма n первых членов геометрической прогрессии (т.е. частная сумма данного ряда) равна 
.
1). Если |q| < 1 (убывающая прогрессия), то 
, тогда 
существует и равен 
– формула суммы бесконечно убывающей геометрической прогрессии.
2). Если |q| > 1, то 
, т.е. не существует, значит, данный ряд расходится.
3). Если q = 1, то данный ряд имеет вид а + а + а +. . .+а + . . . .
В этом случае Sn = a × n: 
, ряд расходится.
4). Если q = – 1, то данный ряд имеет вид а – а + а – а + а –а + . . . .
В этом случае 
.
Следовательно, последовательность Sn вообще не имеет предела и поэтому ряд расходится.
Вывод: Таким образом, при рассмотрении любого числового ряда исследуют его на сходимость.
Остаток сходящегося ряда. Необходимое условие сходимости. Гармонический ряд
Определение. Выражение un+1 + un+2 + un+3 + . . ., обозначаемое Rn, называется остатком (остаточным членом) ряда 
. Очевидно, что каждый ряд можно представить в виде частичной суммы и остатка:
.
Причем Rn, в свою очередь, является числовым рядом, т. к. содержит бесконечное число слагаемых.
Заметим еще, что если ряд сходится, то легко показать, что и его
остаток сходится, т.е. на сходимость ряда не влияет отбрасывание конечного числа первых слагаемых. При исследовании рядов одним из основных вопросов является вопрос о том, сходится ли данный ряд или расходится. Необходимый признак сходимости ряда определяется следующей теоремой.
Теорема 1. Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.
Доказательство.
Пусть ряд u1 + u2 + u3 +. . . + un + . . . сходится, т.е. имеет место равенство 
, где S - сумма ряда (т.е. конечное число), но тогда имеет место также равенство 
, т. к. при n ® ¥ и n – 1 ® ¥. Вычитая почленно из первого равенства второе, получаем:
или 
, но Sn – Sn-–1 = un.
Следовательно,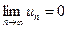 
, что и требовалось доказать.
Следствие. Если n–й член ряда не стремится к нулю при n ® ¥, то ряд расходится.
Пример. Ряд 
расходится, т. к. 
.
Подчеркнем, что рассмотренный признак является только необходимым, но не является достаточным, т.е. из того, что n-й член ряда стремится к нулю, еще не следует, что ряд сходится, – ряд может и расходиться.
Гармоническим называется ряд вида
.
Выясним вопрос о сходимости гармонического ряда. Напишем подробнее гармонический ряд:
Напишем еще вспомогательный ряд:
(1)
Обозначим через 
сумму n первых членов гармонического ряда, через 
– частичную сумму вспомогательного ряда. Так как каждый член гармонического ряда не меньше соответствующего члена ряда (1), то > .
Посчитаем частичные суммы ряда (1) для значений n равных 21, 22, 23, 24, . . ., 2k:
………………………………………………………………………
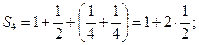
Таким образом, частичные суммы ряда (1) при достаточно большом k могут быть сделаны больше любого положительного числа, т.е. 
, но т.к. > , то 
, т.е. гармонический ряд расходится.
Примем без доказательства, что так называемый обобщенный гармонический ряд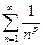 
сходится, если р > 1 и расходится, если р £ 1.