Главная | Обратная связь

Равномерная сходимость

Определение. Сходящийся в промежутке [a, b] функциональный ряд

u₁(х) + u₂(х) + . . . + u_n (х) +. . . =

называется равномерно сходящимся в этом промежутке, если для любого e>0 существует номер N, не зависящий от x и такой, что для всех n>N справедливо неравенство одновременно для всех значений x рассматриваемого промежутка.

Введение в рассмотрение класса равномерно сходящихся рядов целесообразно потому, что последние обладают рядом чрезвычайно важных свойств, заключающихся в непрерывности суммы ряда, в возможности дифференцирования и интегрирования функциональных рядов.

Существует несколько достаточных признаков равномерной сходимости функциональных рядов. Мы рассмотрим один из них.

Признак Вейерштрасса. Ели члены функционального ряда 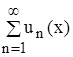в некотором промежутке [a, b] не превосходят по абсолютной величине соответствующих членов сходящегося числового ряда с положительными членами

с₁ + с₂ + . . . + с_n +. . . = ,

т. е. если (n = 1, 2, . . .) для всех х промежутка [a, b], то данный функциональный ряд сходится в этом промежутке абсолютно и равномерно.

Числовой ряд в таком случае называют мажорирующим рядом или числовой мажорантой для функционального ряда 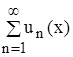в промежутке [a,b].

Пример 1. Доказать, что ряд равномерно сходится на всей числовой оси.

Решение

Так как |sin nx| ≤ 1, то для всех х выполняется неравенство

(n = 1, 2, . . .),

т.е. каждый член ряда не превышает соответствующего члена сходящегося числового ряда . А этот ряд, как известно, сходится. Поэтому в соответствии с определением заключаем, что данный ряд есть равномерно сходящийся ряд.

Очевидно, равномерно сходящимися будут и такие ряды ,

, если только р > 1.

Приведем без доказательства теоремы о свойствах равномерно сходящихся рядов, из которых станет ясной ценность понятия равномерной сходимости ряда.

Теорема 1. Всякий функциональный ряд, равномерно сходящийся в промежутке [a, b], сходится абсолютно в любой точке этого промежутка.

Эта теорема устанавливает связь между равномерной и абсолютной сходимостью функциональных рядов.

Теорема 2. Если члены равномерно сходящегося в промежутке [a, b] функционального ряда

u₁(х) + u₂(х) + . . . + u_n (х) +. . . =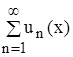

непрерывны, то сумма ряда также непрерывна в промежутке [a, b].

Таким образом, первое свойство конечных сумм целиком переносится на равномерно сходящиеся ряды.

Теорема 3. Если члены равномерно сходящегося на промежутке [a, b] функционального ряда

u₁(х) + u₂(х) + . . . + u_n (х) +. . . = ,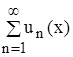

непрерывны на этом промежутке, то ряд можно почленно интегрировать. Это значит, что если х₁ и х₂ – любые две точки промежутка [a, b], то

Если ряд u₁(х) + u₂(х) + … +u_n (х) +…, где u₁(х), u₂(х), …, u_n (х), … – непрерывные функции, равномерно сходится на промежутке [a, b] и имеет сумму S(x), то ряд сходится и имеет сумму , где х₁, х₂ Î [a;b].

Теорема 4. Если члены сходящегося ряда

u₁(х) + u₂(х) + . . . + u_n (х) +. . . =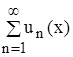

имеют непрерывные производные на промежутке [a, b] и ряд, составленный из этих производных

u₁¢(х) + u₂¢(х) + . . . + u_n¢(х) +. . . = ,

является равномерно сходящимся на промежутке [a, b], то и его сумма равна производной от суммы данного ряда:

[u₁(х) + u₂(х) + . . . + u_n (х) +. . .]¢_x = u₁¢(х) + u₂¢ (х) + . . . + u_n¢ (х) +. . . .

Теорема 5. Если равномерно сходящийся на промежутке [a, b] ряд

u₁(х) + u₂(х) + . . . + u_n (х) +. . . =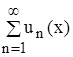

умножить на ограниченную функцию j(х), то полученный ряд

j(х)u₁(х) + j(х)u₂(х) + . . . + j(х)u_n (х) +. . . =

будет равномерно сходящимся на промежутке [a, b].

 

Таким образом, равномерная сходимость функциональных рядов определяет основные важные свойства этих рядов.