Главная | Обратная связь

Разложение в степенной ряд элементарных функций

Чтобы разложить функцию в степенной ряд, необходимо:

1, Найти производные f¢(x). . . f⁽ⁿ⁾(x). . .

2. Вычислить значения f(а), f¢(а), . . . f⁽ⁿ⁾(а), . . .

3. Составить формально степенной ряд

4. Найти интервал сходимости данного ряда.

а) Разложение функции е^х

1. Найдем производные всех порядков

f¢(x) = е^х, . . . . f⁽ⁿ⁾(x) = е^х, . . . .

2. Найдем: f(0) = 1, f¢(0) = 1, . . . . f⁽ⁿ⁾(0) = 1, . . . .

Составим ряд

4. Найдем область сходимости этого ряда

.

Ряд сходится при любом х.

Итак, на всей числовой оси имеем

б)Разложение f(x) = sin x

1. Находим производные:

2. Найдем значения их при х = 0:

f(0) = 0, f ^I(0) = 1, f ^II (0) = 0, f ^III (0) = – 1, f ^IV(0) = 0, f ^V(0) = 1, f ^VI(0) = 0, f ^VII(0) = –1, …

3. Составим ряд

4. Найдем область сходимости полученного ряда.

.

Ряд сходится при любом х, значит, на всей числовой оси имеем

.

(Разложение функций Cos x, ln (1+x), arctg x, (1+x)^m законспектировать на самостоятельной работе.)

в) Разложение функции f(x) = cos x

Так как cosx = (sinx)^¢, то разложение cosx в ряд получим почленным дифференцированием ряда для sinx, при этом область сходимости не изменится.

, или

, –¥ < x < ¥.

г) Разложение функции f(x) = (1 + x)^m (биномиальный ряд), где m – любое действительное число

1. f^/(x) = m (1 + x)^m-1, f^//(x) = m (m – 1)(1 + x)^m–2,

f^///(x) = m (m – 1)(m – 2)(1 + x)^m–3,

f^IV(x) = m (m – 1)(m – 2)(m – 3)(1 + x)^m–4, …

2. f(0) = 1, f^/ (0) = m, f^//(0) = m(m – 1), f^///(0) = m (m – 1)(m – 2)… ,

f⁽ⁿ⁾(0) = m (m – 1)(m – 2)…(m – n + 1), …

3. Составим ряд

4.Найдем область сходимости ряда:

Þ

.

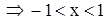д) Разложение функции f(x) = ln(1 + x)

1. Найдем производные:

f ^I(х) = (1 + х)^–1, f ^II(х) = –(1 + х)^–2, f ^III(х) = 1 × 2 × (1 × х)^–3, f^IV(x) = –1 × 2 × 3(1 + x)^–4,

f^V(x) = 1 × 2 × 3 × 4(1 + x)^–5, …, f⁽ⁿ⁾(x) = (–1)ⁿ⁺¹ (n– 1)! (x + 1) ^–n.

2. Найдем их значение при х = 0:

f(0) = ln1 = 0, f^/(0) = 1, f^//(0) = –1!, f^///(0) = 2!, f^IV(0) = –3!, f^V(0) = 4!,…,

f⁽ⁿ⁾(x) = (–1)ⁿ⁺¹ (n– 1)!, … .

3. Составим ряд

.

4. Найдем область сходимости ряда:

.

Исследуем границы:

1) х = –1, –– расходится как гармонический ряд;

2) х = 1, –– сходится по признаку Лейбница.

Итак, при –1 < x £1 имеем

е) Разложение функции f(x) = arctg x

Запишем степенной ряд для функции

этот ряд сходится в интервале – 1< x < 1.

Следовательно, его можно интегрировать по любому промежутку, содержащемуся в указанном интервале.

пусть 0 < x < 1, тогда

для любого х Î ]–1; 1[.

Вывод.Стандартные разложения можно применять для разложения в ряды некоторых сложных функций.