Главная | Обратная связь

Применение степенных рядов в приближенных вычислениях

Степенные ряды находят широкое применение в приближенных вычислениях. С помощью степенных рядов находят приближенные значения определенных интегралов, решают дифференциальные уравнения и т. д. Основой для таких вычислений служит замена бесконечной суммы (ряда) частичной суммой, отбрасывая остаточный член, т.е. вместо S = S_n + R_n берут S » S_n , например, .

При этом погрешность определяется величиной R_n, поэтому, если имеем дело со знакочередующимся рядом, то |R_n| по теореме Лейбница не превосходит величины первого "отброшенного" члена.

Если ряд не является знакочередующимся, значит, надо использовать, например, форму Лагранжа для остаточного члена.

Ряды

, (7)

sin x = x - - (8)

cos x = 1 - (9)

можно использовать для вычисления значений e^x, sinx и cosx при любых значениях x с любой степенью точности, поскольку указанные равенства выполняются на всей оси x.

Если в качестве приближённых значений этих функций брать частичные суммы рядов (7) – (9) соответственно, то допускаемые при этом погрешности особенно просто оцениваются в случае рядов (8) и (9), в силу признака Лейбница погрешность не превосходит первого из отброшенных членов.

Ряд для логарифма

ln (1+x) = x - -1 < x £ 1, (10)

хотя и знакопеременный, но сходится медленно, а при x > 1 расходится. Чтобы ускорить сходимость ряда и сделать возможным вычисление логарифмов чисел, больших единицы, из разложения (10) вычитают разложение

ln (1-x) = -x -

Это даёт

ln ( ) = 2x (1+ ). (11)

Полагая в (11) x = , получают:

ln = 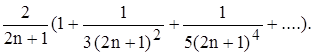(12)

Отправляясь от ln 1 = 0, можно с помощью ряда (12), сходящегося достаточно быстро, найти логарифмы всех натуральных чисел.

Ряд для арктангенса arctg x = x - (13)

можно использовать, например, для вычисления числа p с любой степенью точности. Именно, полагая в (13) x = 1, получим

В силу знакопеременности этого ряда легко оценивается погрешность, допускаемая при замене ряда частичной суммой.

Пример. Вычислить интеграл с точностью до D = 0,001.

Решение.

Используя разложение (7), получим разложение подынтегральной функции

Интегрируем полученное равенство на промежутке[0; 1].

=

= =

Получили сходящийся знакочередующийся ряд. Если вместо него взять 3 первых слагаемых, то "отброшенная" часть (тоже – сходящийся ряд) не превосходит по величине первого "отброшенного" слагаемого, т.е. .

Итак, .

Вывод:При разложении функций в степенные ряды удобно применять стандартные разложения.