Главная | Обратная связь

Необходимый признак сходимости. Гармонический ряд.

Теорема 14.1.5. Если ряд сходится, предел его общего члена при n®¥ равен нулю, т.е. (14.1.4)

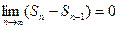Доказательство. Так как ряд сходится, то и . Тогда , но , откуда

Следствие. Если , ряд расходится.

Пример Исследовать на сходимость ряд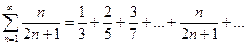

, ряд расходится.

Замечание. Следует иметь в виду, что утверждение, обратное необходимому признаку сходимости неверно. Признак недостаточен для сходимости ряда. Из условия не следует, что ряд сходится.

сходится

ряд сходится

В качестве примера рассмотрим гармонический ряд .

Как видим, , т.е. выполнен необходимый признак сходимости. Покажем, что при этом гармонический ряд расходится. Рассмотрим частичные суммы S_n и S_2n

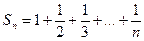
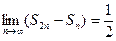(14.5)

Предположим, гармонический ряд сходится.

В этом случае и и , что противоречит равенству (14.5). Следовательно, предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится.

Знакоположительные ряды. Достаточные признаки

Сходимости.

Теорема 14.1.6 (признак сравнения)

Пусть даны два ряда с положительными членами и , причем каждый член ряда (А) не превосходит соответствующего члена ряда (B), т.е. при любом n an £ bn (14.1.6)

Тогда:

а) если сходится ряд (B), то сходится и ряд (А), причем сумма ряда (А) не превосходит суммы ряда (B);

б) если расходится ряд (А), то расходится и ряд (В).

Доказательство

а) Пусть S_n(А) и S_n(B) – частичные суммы рядов (А) и (В) соответственно, S(B) – сумма ряда (B), т.е. существует предел . Очевидно, в силу неравенства (14.6), а , т.к. все члены ряда (B) положительны (b_n>0).

Из обоих неравенств следует , т.е. последовательность частичных сумм ряда (А) ограничена. Кроме того, последовательность частичных сумм ряда (А) монотонно возрастает, т.к. все а_n>0, откуда

Следовательно, на основании признака существования предела (5.3.6) существует , т.е. ряд (А) сходится.

Из условия на основании свойства ( т. 5.1.4) пределов получаем 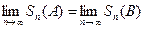, т.е , что и требовалось доказать.

б) пусть ряд (А) расходится, т.е 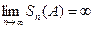, но из условия (14.1.6) . Переходя к пределу, получаем , а это означает, что , т.е. ряд (B) расходится.

Примеры. Исследовать сходимость рядов.

1.

Сравним данный ряд с гармоническим рядом 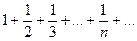Достаточно сравнить общие члены рядов. Очевидно , но гармонический ряд расходится, следовательно, и данный ряд также расходится.

2.

Сравним данный ряд со следующим рядом:

Этот ряд сходится, как геометрическая прогрессия со знаменателем . Т.к. , тогда и данный ряд сходится.

Недостаток признака сравнения заключается в необходимости привлекать другие ряды, что бывает не всегда просто, и относительно которых также следует решать вопросы их сходимости. Кроме того, необходимо доказывать в каждом случае выполнимость неравенства (14.6). Однако достаточно часто удобно использовать эталонные ряды, к которым можно отнести сходящийся геометрический ряд (прогрессия) при |q|<1, гармонический ряд и обобщенный гармонический ряд , который сходится, если <1 и расходится, если ³1 (было показано выше)

Наряду с рассмотренным признаком сравнения рассмотрим еще один.

Теорема 14.1.7 (предельный признак сравнения).

Если и – ряды с положительными членами и существует конечный предел отношения их общих членов , то оба ряда одновременно сходятся, либо расходятся (ведут себя одинаково)

Доказательство. Пусть .

По определению предела числовой последовательности (тема 5.1) для любого e>0 существует такой номер N, что для всех n>N выполняется неравенство , которое можно записать следующим образом , или (14.1.7)

Используем признак сравнения и свойства сходящихся рядов применительно к двойному неравенству (14.1.7). Если ряд сходится, то сходится и ряд (теорема 14.1.2). Но на основании признака сравнения сходится и ряд . Предположим, сходится ряд , но тогда сходится и ряд , а значит и сходится и ряд . Предположим ряд расходится, но тогда расходится и ряд , а следовательно расходится и ряд ; если расходится , то аналогично рассуждая, получаем, что расходится и ряд .

Пример. Исследовать сходимость ряда .

Сравним с рядом , который сходится ( )

Теорема 14.1.8. Пусть даны два ряда (А) и (В). Если хотя бы начиная с некоторого номера выполняется неравенство , то если сходится ряд (В), то сходится и ряд (А); если расходится ряд (А), то расходится и ряд (В).

Доказательство. Пусть , , … .

Тогда или . Если ряд сходится, то сходится и ряд , следовательно на основании признака сравнения (теорема 6) сходится и ряд , значит, сходится и ряд (А) . Если расходится ряд (А), то расходится и ряд , а значит, и ряд . Но тогда расходится и ряд (В).

Выше было отмечено, что признаки сравнения неудобны тем, что требуют привлечения других рядов, желательно хорошо знакомых, которых не так много. Целесообразно рассмотреть признаки, когда ряд как бы говорил сам за себя.

Признак Даламбера

Теорема 14.1.9. Пусть дан ряд с положительными членами и существует предел отношения (n+1)-го к n-му члену: . Если l<1, ряд сходится; если l>1, расходится; если l=1, вопрос о поведении ряда остается нерешенным.

Доказательство. Из определения предела следует, что для любого e>0 существует такой номер N, начиная с которого выполняется неравенство . После преобразования получаем, что для n>N .

1) Пусть l<1, и q – любое число, удовлетворяющее условию l<q<1.

^{0 l q 1}

Выберем e=q-l>0. Тогда для n>N выполняется неравенство , т.е. a_n+1<a_nq. Это неравенство запишем для n>N.

a_N+1<qa_N, , a_N+2<a_N+1q<a_Nq²,… a_N+k<a_Nq^k,…

Chfdybv lfyysq hzl a₁+a₂+a₃+…+a_N+a_N+1+a_N+2+…+a_N+k+… c utjvtnhbxtcrbv hzljv a_N+qa_N+q²a_N+…+q^ka_N…

Этот геометрический ряд сходится, т.к. |q|<1. Следовательно, на основании признака сравнения сходится ряд, полученный из данного ряда путем отбрасывания первых N членов. Но тогда в соответствии со свойствами сходящихся рядов (теорема 14.1.1) сходится и данный ряд ;

2) Пусть l>1.

0 1 l-e l l+e

Если , то существует такой номер N, начиная с которого, дроби

попадают в сколь угодно малую e-окрестность точки l и, следовательно, для n>N дроби принимают значения большие единицы, т.е. или . Это означает, что члены ряда возрастают, начиная с номера N+1, т.е. не выполняется необходимый признак сходимости и ряд расходится.

Примеры. Исследовать сходимость рядов.

1.

, , – ряд сходится

2. , , ,

– ряд расходится

3. , .

О поведении ряда ничего нельзя сказать, если использовать признак Даламбера. Но можно заметить, что , т.е. не выполняется необходимый признак сходимости. Ряд расходится.

4.

Используем признак Даламбера. .

О поведении ряда ничего сказать нельзя. Используем другие способы определения сходимости. Преобразуем общий член ряда . Найдем частичную сумму ряда . .

Существует предел частичной суммы. Значит, ряд сходится, и его сумма равна 1.

Сравнение рассматриваемых рядов с геометрическим рядом позволяет доказать их сходимость (расходимость).

Признак Коши

Теорема 14.1.10.Пусть дан ряд с положительными членами и существует предел . Если l<1, ряд сходится; если l>1, ряд расходится; если l=1, вопрос о сходимости ряда остается не решенным.

Доказательство(аналогично доказательству теоремы Даламбера).

Из определения предела следует: для любого e>0 существует такой номер N, что для всех n>N, то выполняется неравенство .

1) Пусть l<1 и q ­– любое число, удовлетворяющее условию l<q<1. Примем e=q-l. Тогда , или для n>N, откуда a_n<qⁿ. Придавая n значения N+1, N+2, …, N+k, получаем a_n+1<q^N+1, a_n+2<q^N+2, …, a_n+k<q^N+k, … От данного ряда отбросим первые N членов. Получаем ряд a_n+1 + a_n+2 +…+a_n+k+… Сравним этот «отсеченный» ряд с рядом q^N+1 + q^N+2 +…+ q^N+k +…, который представляет собой сходящийся геометрический ряд, так как его знаменатель q₀<q<1. Так как члены «отсеченного» ряда меньше соответствующих членов геометрического ряда, то по признаку сравнения «отсеченный» ряд сходится. Но тогда сходится и данный ряд (теорема 14.1.3).

2) l>1. В этом случае (см. признак Даламбера) члены ряда, начиная с номера N попадают в окрестность точки l, т.е. становятся больше единицы: a_n>1. Тем самым не выполняется необходимый признак сходимости. Ряд расходится.

Примеры. Исследовать на сходимость ряды.

1.

Найдем , ряд сходится.

2.

Найдем , ряд расходится.