Главная | Обратная связь

Знакочередующиеся ряды. Признак Лейбница.

Ряд вида a₁-a₂+a₃-a₄+…+(-1)^n-1∙a_n+…, где a_n>0 называется знакочередующимся.

Теорема 14.1.12 (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине (a1>a2>a3>…>an>…) и предел общего члена при n→¥ равен нулю, т.е. , то ряд сходится и его сумма не превосходит первого члена: S ≤ a1.

Доказательство

Пусть a_n> a_n+1 и . Рассмотрим последовательность четных частичных сумм (n=2m), записав ее в виде

S_n=S_2m=a₁-(a₂-a₃)-(a₄-a₅)-…-(a_2m-2-a_2m-1)-a_2m

Все выражения, стоящие в скобках, положительны, откуда следует что S_2m<a₁, т.е. последовательность четных частичных ограничена.

Рассмотрим следующую четную частичную сумму

S_2m+2<S_2m+(a_2m+1-a_2m+2)>S_2m. Это означает, что последовательность четных частичных сумм монотонно возрастает. На основании признака существования пределов (т.5.3.6) существует .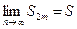

Рассмотрим последовательность нечетных частичных сумм.

S_2m+2=S_2m+a_2m+1

Переходя к пределу при n→¥, получаем

Итак, при любом n (четном и нечетном) при n→¥ существует , т.е. знакочередующийся ряд сходится.

Геометрическая интерпретация признака Лейбница 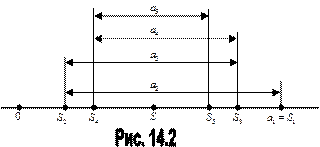На рис. 14.2 видно, что последовательность частичных сумм сходится к числу S слева, если n – четное и справа, если n – нечетное, при этом S2m<S<S2m+1. В любом случае S≤a1. Следствие. Найдем остаток знакочередующегося ряда S-Sn=rn, который, в свою очередь, представляет знакочередующийся ряд (-1)n∙(an+1–an+2+an+3-…), который сходится (т. 14.1.2) и его сумма , т.е. . Иными словами: абсолютная погрешность, получающаяся при замене суммы сходящегося знакочередующегося ряда его частичной суммой, не превосходит по абсолютной величине первого из отброшенных членов, т.е. S≈Sn и погрешность .

Пример. Исследовать сходимость ряда.

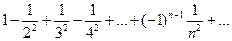
Видим, что члены ряда по абсолютной величине убывают, и .

Ряд сходится и его сумма S<1.

а) Найти сумму этого ряда, ограничившись четырьмя членами, т.е. n=4.

, при этом погрешность

Таким образом, можно сказать, что сумма ряда 0,759<S<0,839.

б) Найти сумму данного ряда с точностью до 0,025. Задача сводится к отысканию такого значенияn (числа членов), когда 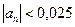, т.е. или , откуда , т.к. n– целое, то n = 7. Итак . Следовательно, для того, чтобы обеспечить заданную точность, достаточно ограничиться шестью членами, т.е.

и