 |
|
Разложение в ряд Маклорена некоторых элементарных функций
1. y=ex
Находим производные различных порядков:
x=0
По (15.11) получаем
(15.2.5)
Радиус сходимости этого ряда 
, т.е. ряд (15.2.5) сходится к функции ex на всей числовой оси.
2. 
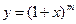, где m – любое рациональное число
……………………………… ………………………
……………………………………………………………………………
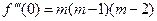
На основании (15.10) получаем ряд Маклорена для функции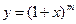
(15.2.6
Ряд (15.2.6) называется биномиальным рядом. Его радиус сходимости
,
т.е. ряд сходится в интервале (-1,1).
Замечание: если m – целое, положительное число, то биномиальный ряд представляет собой многочлен степени m, так как при m-n+1=0. n-ый член ряда (15.2.6) и все остальные члены равны нулю. Этот многочлен называется биномом Ньютона.
3. 
.
Представим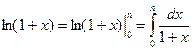 
Подынтегральную функцию 
будем рассматривать как геометрический ряд с первым членом, равным единице, и знаменателем 
, который сходится, если 
, т.е. в интервале (-1,1). Это означает, что
(15.2.7)
Интегрируя почленно ряд (15.2.7), получаем разложение в ряд функции
, (15.2.8)
который сходится внутри интервала (-1,1). Сходимость на концах интервала требует дополнительного исследования.
Используя ряды (15.2.5) – (15.2.8), можно достаточно просто находить разложения в ряд более сложных функций, не прибегая к их многократному дифференцированию, что может быть достаточно сложно.
Примеры. Разложить в ряд функции
1. 
. Воспользуемся разложением (15.2.7)
2. 
. Воспользуемся биномиальным рядом, полагая 
, подставив 
вместо 
,
3. 
. Воспользуемся рядом (15.2.4)
Во всех случаях следует дополнительно исследовать сходимость рядов на концах интервала сходимости.
Используя ряды (15.2.5) – (15.2.8) и приведенные примеры, можно достаточно просто получать разложения в ряд функций 
, 
, 
, 
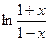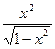и т.п.
Приложения рядов в приближенных вычислениях.
Ряды Маклорена (Тэйлора) могут быть использованы для приближенного вычисления значений функций, определенных интегралов (в том числе «неберущихся», что особенно актуально), решения дифференциальных уравнений и т.д.