Главная | Обратная связь

Сходимость рядов с положительными членами

Ряды

 

Методические указания и индивидуальные

задания для выполнения типового расчета

 

Хабаровск

Издательство

 

 

УДК 517.521(075.8)

ББК В161.3 я 73

Г 701

Рецензент

Кандидат физико – математических наук

доцент кафедры «Высшая математика» Дальневосточный государственный университет путей сообщения, Э.Д. Кононенко

 

 

Городилова М.А.

Г 701 Ряды.: Метод. указания /М.А.Городилова, Г.В.Костина.- Хабаровск: Изд-во ДВГУПС, 1998. -38 с.:ил.

 

В методических указаниях изложены общие теоретические положения по теме «Числовые и степенные ряды».

Подробно рассмотрены примеры из всех разделов этой темы. Даны варианты индивидуальных заданий.

Указания предназначены для студентов всех специальностей железнодорожного вуза.

Список лит. - 7 назв.

 

 

© ГОУ ВПО «Дальневосточный государственный университет

путей сообщения МПС России» (ДВГУПС), 2005

 

РЯД И ЕГО СУММА

Числовым рядом называется выражение вида:

a₁ + a₂ + a₃ + ... + a_n + ... = (1)

где: a_1, a_2, a_3, ... a_n ... образуют бесконечную числовую последовательность.

a_n - общий член ряда.

Сумма n первых членов ряда называется n-ой частичной суммой ряда и обозначается S_n .

S_n = a₁ + a₂ + a₃ + ... + a_n

Если существует конечный предел S = , то ряд называется сходящимся, а S - суммой ряда.

Ряд называется расходящимся, если не существует (в частности, если = ).

Особое значение имеет задача об исследовании ряда на сходимость.

 

Теорема (необходимый признак сходимости ряда)

 

Если ряд (1) сходится, то предел его общего члена равен нулю:

= 0

Отсюда вытекает, что если 0, то ряд расходится. Если же = 0, то о сходимости ряда еще ничего сказать нельзя.

 

Пример 1. Можно ли с помощью необходимого признака решить вопрос о сходимости ряда?

 

а)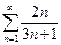

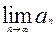= = = 0

значит данный ряд расходится.

 

б)

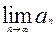= = = 0

т.е. о сходимости данного ряда еще ничего сказать нельзя.

Сходимость рядов с положительными членами

 

Если необходимый признак не дает ответа на вопрос о сходимости числового ряда (1), следующие достаточные признаки позволяют судить об этом.

 

Первый признак сравнения

Пусть даны ряды и с положительными членами, причем начиная с некоторого номера n . Тогда из сходимости ряда следует сходимость ряда ; из расходимости ряда следует расходимость ряда .

Сравнение исследуемых рядов производится обычно с некоторыми стандартными рядами:

а) , (геометрическая прогрессия, сходящаяся при 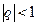и расходящаяся при ).

б) (обобщенный гармонический ряд, сходящийся при и расходящийся при ).

 

Пример 2. Исследовать на сходимость ряд .

Сравнивая общий член данного ряда с общим членом расходящегося гармонического ряда , убеждаемся что при всех n. Следовательно исследуемый ряд расходится.

Второй признак сравнения. Если сходимость ряда известна и существует конечный и отличный от нуля предел , то оба ряда либо одновременно сходятся, либо одновременно расходятся. Если же =0, то из сходимости ряда следует сходимость ряда .

Пример 3. Исследовать на сходимость ряд . Сравним данный ряд со сходящимся рядом :

: = = ,

т.е. ряд тоже сходится.

Признак Даламбера. Если существует предел , то при < 1 ряд сходится , а при > 1 - расходится. При = 1 ряд может сходиться или расходиться.

 

Пример 4. Исследовать ряд на сходимость с помощью признака Даламбера.

а)

; следовательно, ряд сходится.

б)

= = 3>1; значит ряд расходится.