 |
|
Приложения степенных рядов
Рядом Тейлора для функции f(x) в окрестности точки  называется степенной ряд относительно двучлена (x-
называется степенной ряд относительно двучлена (x-  ) вида
) вида

При  =0 ряд Тейлора есть степенной ряд относительно переменной х:
=0 ряд Тейлора есть степенной ряд относительно переменной х:

который называется рядом Маклорена.
Ряд Тейлора можно записать для любой функции f(x), которая в окрестности точки 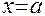 имеет производные любого порядка. Однако этот ряд представляет данную функцию f(x) только тогда, когда остаточный член ряда будет стремиться к нулю.
имеет производные любого порядка. Однако этот ряд представляет данную функцию f(x) только тогда, когда остаточный член ряда будет стремиться к нулю.
При решении многих задач рекомендуется пользоваться следующими разложениями элементарных функций:




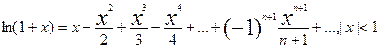
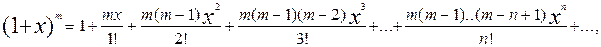

Пример10. Разложить функцию в ряд Маклорена, используя разложения элементарных функций.
а) 

 =
= 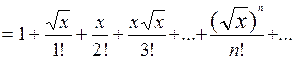
Ряд сходится к данной функции при всех значениях х.
б) sin2x
sin2x= 

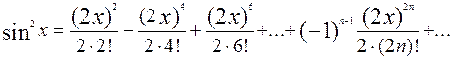
Ряд сходится при всех значениях х.
в) ln(3+x)
Преобразуем аргумент функции.
ln(3+x)=  .
.
Воспользуемся разложением функции ln(1+t), полагая t=x/3
ln(3+x)=ln3+ 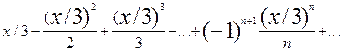
Так как разложение ln(1+t) имеет место при |t|<1, то данное разложение будет иметь место при |x/3|<1, то есть |x|<3
Пример 11. Пользуясь соответствующими рядами, вычислить с точностью до 0,0001.
а) 
 =
= 
Применим биномиальный ряд, полагая х=1/16, m=1/4:

Чтобы определить, сколько взять первых членов этого знакочередующегося ряда для вычисления  с точностью до 0,0001, вычислим
с точностью до 0,0001, вычислим
 =1;
=1; 
Ошибка искомого приближенного значения корня будет меньше 0,0001.Значит
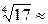 2(1+0,01562-0,00037)
2(1+0,01562-0,00037) 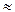 2,0305.
2,0305.
б) 
Так как
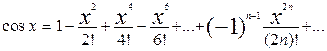 ,
,
то  =
=
= 
Пятый член этого знакочередующегося ряда меньше 0,0001. Поэтому для вычисления искомого приближенного значения достаточно взять сумму первых четырех первых членов ряда, т.е. 
ИНТЕГРИРОВАНИЕ дифференциальных уравнений С
ПОМОЩЬЮ рядов
Пусть требуется найти решение уравнения
y' = f(x, y), (1)
удовлетворяющее начальному условию y(x0)=y0. Будем искать решение уравнения в виде:
y= y(x0)+  (2)
(2)
Свободный член y(x0) этого разложения известен: он равен y0. Подставив в (1) значение x=x0, найдем и y'(x0)= f(x0, y0).
Далее, дифференцируя (1), получаем y''=fx'(x, y)+fy'(x, y)y', (3)
откуда находим y''(x0).
Аналогично этому, дифференцируя (3) найдем y'''(x0) и т.д.
Пример 12. Представить решение уравнения в виде первых шести членов ряда.
y'=x-y2, (4)
удовлетворяющее начальному условию y(1)=1.
Последовательно дифференцируя равенство (4), находим
y''=1- y' 2y,
y'''=-2(y')2-2yy'',
y(4)=-6y'y''-2yy'',
y(5)=-6(y'')2-8y'y'''-2yy(4),
y(6)= -20y''y'''-10y'y(4)-2yy(5),
Отсюда из (4) получаем
y'(1)=0, y''(1)=1, y'''(1)=-2, y(4)=4, y(5)=-14, y(6)=68.
Значит,
y=1+ 
Ряды Фурье.
Рядом Фурье для функции f(x) в интервале  называется тригонометрический ряд вида:
называется тригонометрический ряд вида:
 +
+  ,
,
если его коэффициенты an и bn вычисляются по формулам Фурье:
an = 
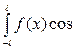
 dx, n = 0,1,2, ..., а0 =
dx, n = 0,1,2, ..., а0 = 
bn = 
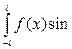
 dx, n = 1,2, ...
dx, n = 1,2, ...
Если в интервале  функция f(x) имеет конечное число точек разрыва первого рода (или непрерывна) и конечное число точек экстремума (или не имеет их вовсе), то ее ряд Фурье сходится, т.е. имеет сумму S(x)во всех точках этого интервала.
функция f(x) имеет конечное число точек разрыва первого рода (или непрерывна) и конечное число точек экстремума (или не имеет их вовсе), то ее ряд Фурье сходится, т.е. имеет сумму S(x)во всех точках этого интервала.
При этом:
а) в точках непрерывности функции f(x) он сходится к самой функции, S(x)=f(x);
б) в каждой точке разрыва функции - к полусумме односторонних пределов функции слева и справа.
Если функция четная, т.е. f(x)=f(-x), все коэффициенты bn = 0 и ряд имеет вид:
f(x)=  +
+  ,
,
 =
= 
 cos
cos  dx, n=0,1,2, ...
dx, n=0,1,2, ...
Если функция нечетная, т.е. f(x)=-f(-x), все коэффициенты  = 0, и ряд имеет вид:
= 0, и ряд имеет вид:
f(x) = 
 ,
, 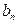 =
= 


 dx, n=1,2,3, ...
dx, n=1,2,3, ...
Замечания
1. Функция, заданная в интервале [0;  ], может быть разложена в зависимости от требований либо только в ряд косинусов, либо только в ряд синусов. Для этого она должна быть продолжена в интервале [-
], может быть разложена в зависимости от требований либо только в ряд косинусов, либо только в ряд синусов. Для этого она должна быть продолжена в интервале [-  ; 0] либо как четная, либо как нечетная.
; 0] либо как четная, либо как нечетная.
2. Если функция f(x) задана несколькими различными формулами на разных частях интервала  , то при вычислении интегралов для коэффициентов ряда, следует разбить интервал интегрирования точками, в которых меняется аналитическое выражение функции, на части и затем вычислять указанные интегралы как сумму интегралов по составляющим частям.
, то при вычислении интегралов для коэффициентов ряда, следует разбить интервал интегрирования точками, в которых меняется аналитическое выражение функции, на части и затем вычислять указанные интегралы как сумму интегралов по составляющим частям.
Пример 13. Разложить в ряд Фурье данную функцию в указанном интервале.
а) f(x) =  , 0<x<4, T=4.
, 0<x<4, T=4.
Поскольку интервал (0,4) не симметричен относительно нуля и имеет длину равную 4, то формулы для коэффициентов Фурье принимают вид:
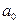 =
= 

 =
= 
 cos
cos  dx,
dx,
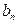 =
= 
 sin
sin  dx.
dx.
Вычислим интегралы.
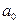 =
= 
 =
=  =2
=2
 =
= 

 dx =
dx =  x = u, du = dx, dv = cos
x = u, du = dx, dv = cos  dx, V =
dx, V = 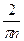 sin
sin 
 =
= 
 =
= 
 = 0
= 0
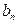 =
=  sin
sin  dx =
dx =  x = u, du = dx, dv = sin
x = u, du = dx, dv = sin  dx, V =
dx, V =  cos
cos 
 =
= 
 =
= 
 =
= 
следовательно,
 = 1 +
= 1 +  =
= 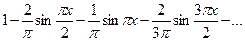
Это разложение справедливо, т.е. полученный ряд сходится к данной функции во всех точках ее области определения 0<x<4. В граничных точках x=0 и x=4 сумма ряда равна 1, в этих точках все члены ряда, кроме первого, обращаются в 0. График суммы ряда изображен на рис.1

Рис. 1
б) f(x)=xsin(x), 0<x<p в ряд по косинусам.
Функция, разлагаемая в ряд по косинусам, должна быть четная. Следовательно, нужно построить ее четное продолжение в интервале (-p,0) . Тогда bn = 0.
 =
= 
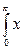 sin xdx =
sin xdx =  х = u, du = dx, sin xdx = dV, V =
х = u, du = dx, sin xdx = dV, V = 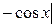 =
= 

 +
+  =
= 
 = 2
= 2
 =
=  =
= 


 =
=  =
=
 =
= 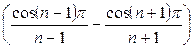 =
=  =
=  =
=  =
=  ,
, 
При n=1
 =
=  =
= 

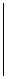 =
=  =
= 
Следовательно,  =
=  . Это разложение данной периодической и всюду непрерывной функции справедливо при любом значении x, т.е. полученный ряд Фурье сходится к данной функции на всей числовой оси.
. Это разложение данной периодической и всюду непрерывной функции справедливо при любом значении x, т.е. полученный ряд Фурье сходится к данной функции на всей числовой оси.
Варианты индивидуальных заданий
1. Найти  и
и  члены ряда
члены ряда
| 1.1. | 3+ 
|
| 1.2 | 
|
| 1.3 | 
|
| 1.4 | 
|
| 1.5 | 
|
| 1.6 | 
|
| 1.7 | 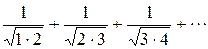
|
| 1.8 | 
|
| 1.9 | 
|
| 1.10 | 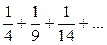
|
| 1.11 | 
|
| 1.12 |  +… +…
|
| 1.13 | 
|
| 1.14 | 
|
| 1.15 |  
|
| 1.16 | 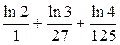 +… +…
|
| 1.17 | 
|
| 1.18 | 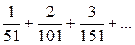
|
| 1.19 | 
|
| 1.20 | 
|
| 1.21 | 
|
| 1.22 | 
|
| 1.23 | 
|
| 1.24 | 
|
| 1.25 | 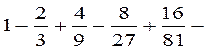 … …
|
| 1.26 |  … …
|
| 1.27 | 
|
| 1.28 | 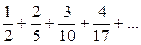
|
| 1.29 | 
|
| 1.30 |  +… +…
|
2. Найти сумму ряда
| 2.1 | 
| 2.16 | 
|
| 2.2 | 
| 2.17 | 
|
| 2.3 | 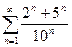
| 2.18 | 
|
| 2.4 | 
| 2.19 | 
|
| 2.5 | 
| 2.20 | 
|
| 2.6 | 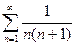
| 2.21 | 
|
| 2.7 | 
| 2.22 | 
|
| 2.8 | 
| 2.23 | 
|
| 2.9 | 
| 2.24 | 
|
| 2.10 | 
| 2.25 | 
|
| 2.11 |  
| 2.26 | 
|
| 2.12 | 
| 2.27 | 
|
| 2.13 | 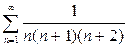
| 2.28 | 
|
| 2.14 | 
| 2.29 | 
|
| 2.15 | 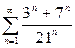
| 2.30 | 
|
3. Можно ли решить вопрос о сходимости ряда с помощью необходимого признака?
| 3.1 | a) | 
| b) | 
|
| 3.2 | a) | 
| b) | 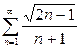
|
| 3.3 | a) | 
| b) | 
|
| 3.4 | a) | 
| b) | 
|
| 3.5 | a) | 
| b) | 
|
| 3.6 | a) | 
| b) | 
|
| 3.7 | a) | 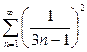
| b) | 
|
| 3.8 | a) | 
| b) | 
|
| 3.9 | a) | 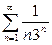
| b) | 
|
| 3.10 | a) | 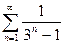
| b) | 
|
| 3.11 | a) | 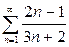
| b) | 
|
| 3.12 | a) | 
| b) | 
|
| 3.13 | a) | 
| b) | 
|
| 3.14 | a) | 
| b) | 
|
| 3.15 | a) | 
| b) | 
|
| 3.16 | a) | 
| b) | 
|
| 3.17 | a) | 
| b) | 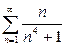
|
| 3.18 | a) | 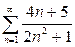
| b) | 
|
| 3.19 | a) | 
| b) | 
|
| 3.20 | a) | 
| b) | 
|
| 3.21 | a) | 
| b) | 
|
| 3.22 | a) | 
| b) | 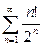
|
| 3.23 | a) | 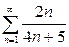
| b) | 
|
| 3.24 | a) | 
| b) | 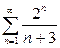
|
| 3.25 | a) | 
| b) | 
|
| 3.26 | a) | 
| b) | 
|
| 3.27 | a) | 
| b) | 
|
| 3.28 | a) | 
| b) | 
|
| 3.29 | a) | 
| b) | 
|
| 3.30 | a) | 
| b) | 
|
4. Исследовать ряды на сходимость
| 4.1 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.2 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.3 | |||||||
| a) | 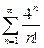
| б) | 
| в) | 
| г) | 
|
| 4.4 | |||||||
| a) | 
| б) | 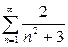
| в) | 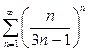
| г) | 
|
| 4.5 | |||||||
| a) | 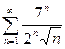
| б) | 
| в) | 
| г) | 
|
| 4.6 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.7 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.8 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.9 | |||||||
| a) | 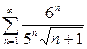
| б) | 
| в) | 
| г) | 
|
| 4.10 | |||||||
| a) | 
| б) | 
| в) | 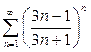
| г) | 
|
| 4.11 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 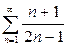
|
| 4.12 | |||||||
| a) | 
| б) | 
| в) | 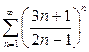
| г) | 
|
| 4.13 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.14 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.15 | |||||||
| a) | 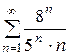
| б) | 
| в) | 
| г) | 
|
| 4.16 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 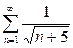
|
| 4.17 | |||||||
| a) | 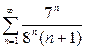
| б) | 
| в) | 
| г) | 
|
| 4.18 | |||||||
| a) | 
| б) | 
| в) | 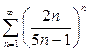
| г) | 
|
| 4.19 | |||||||
| a) | 
| б) | 
| в) | 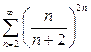
| г) | 
|
| 4.20 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 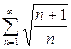
|
| 4.21 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.22 | |||||||
| a) | 
| б) | 
| в) | 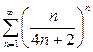
| г) | 
|
| 4.23 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.24 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 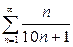
|
| 4.25 | |||||||
| a) | 
| б) | 
| в) | 
| г) | 
|
| 4.26 | |||||||
| a) | 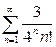
| б) | 
| в) | 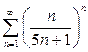
| г) | 
|
| 4.27 | |||||||
| a) | 
| б) | 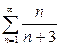
| в) | 
| г) | 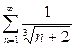
|
| 4.28 | |||||||
| a) | 
| б) | 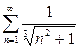
| в) | 
| г) | 
|
| 4.29 | |||||||
| a) | 
| б) | 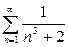
| в) | 
| г) | 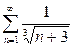
|
| 4.30 | |||||||
| a) | 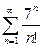
| б) | 
| в) | 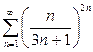
| г) | 
|
5.Выяснить, сходится ряд абсолютно или условно
| 5.1 | a) 
| b) 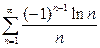
| 5.16 | a) 
| b) 
|
| 5.2 | a) 
| b) 
| 5.17 | a) 
| b) 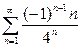
|
| 5.3 | a) 
| b) 
| 5.18 | a) 
| b) 
|
| 5.4 | a) 
| b) 
| 5.19 | a) 
| b) 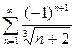
|
| 5.5 | a) 
| b) 
| 5.20 | a) 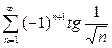
| b) 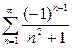
|
| 5.6 | a) 
| b) 
| 5.21 | a) 
| b) 
|
| 5.7 | a) 
| b) 
| 5.22 | a) 
| b) 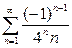
|
| 5.8 | a) 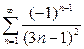
| b) 
| 5.23 | a) 
| b) 
|
| 5.9 | a) 
| b) 
| 5.24 | a) 
| b) 
|
| 5.10 | a) 
| b) 
| 5.25 | a) 
| b) 
|
| 5.11 | a) 
| b) 
| 5.26 | a) 
| b) 
|
| 5.12 | a) 
| b) 
| 5.27 | a) 
| b) 
|
| 5.13 | a) 
| b) 
| 5.28 | a) 
| b) 
|
| 5.14 | a) 
| b) 
| 5.29 | a) 
| b) 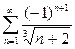
|
| 5.15 | a) 
| b) 
| 5.30 | a) 
| b) 
|
6. Определить интервал сходимости ряда и исследовать сходимость на концах интервала
| 6.1 | a) 
| б) 
| в) 
|
| 6.2 | a) 
| б) 
| в) 
|
| 6.3 | a) 
| б) 
| в) 
|
| 6.4 | a) 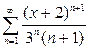
| б) 
| в) 
|
| 6.5 | a) 
| б) 
| в) 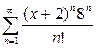
|
| 6.6 | a) 
| б) 
| в) 
|
| 6.7 | a) 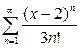
| б) 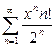
| в) 
|
| 6.8 | a) 
| б) 
| в) 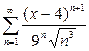
|
| 6.9 | a) 
| б) 
| в) 
|
| 6.10 | a) 
| б) 
| в) 
|
| 6.11 | a) 
| б) 
| в) 
|
| 6.12 | a) 
| б) 
| в) 
|
| 6.13 | a) 
| б) 
| в) 
|
| 6.14 | a) 
| б) 
| в) 
|
| 6.15 | a) 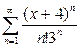
| б) 
| в) 
|
| 6.16 | a) 
| б) 
| в) 
|
| 6.17 | a) 
| б) 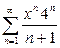
| в) 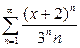
|
| 6.18 | a) 
| б) 
| в) 
|
| 6.19 | a) 
| б) 
| в) 
|
| 6.20 | a) 
| б) 
| в) 
|
| 6.21 | a) 
| б) 
| в) 
|
| 6.22 | a) 
| б) 
| в) 
|
| 6.23 | a) 
| б) 
| в) ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
|