 |
|
Понятие ряда и его суммы. Необходимый признак сходимости ряда
А. А. ГОЛУБЕВ
ЧИСЛОВЫЕ РЯДЫ
Учебно-методическая разработка
для студентов I курса
ТВЕРЬ 2012
Рассматриваются понятия числового ряда и его сходимости. Предназначено для студентов математических факультетов. При написании использовалась рукопись Смирнова Геннадия Аркадьевича.
Печатается по решению кафедры математического анализа Тверского государственного университета.
 |
Понятие ряда и его суммы. Необходимый признак сходимости ряда
Определение 1. Пусть дана последовательность комплексных чисел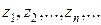 
Символ вида
(1)
называют числовым рядом.
Числа 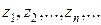называют первым, вторым и т.д. членами ряда. Выражение 
называют n-м или общим членом ряда.
Заметим, что в определении 1 числа 
, в частности, могут быть действительными.
Примеры. 1) 
, общий член ряда равен 
;
2) 
, 
;
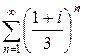3) 
, 
;
4) 
, 
.
Пусть дан ряд (1). Образуем последовательность чисел:
;
;
;
;
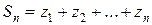Последовательность 
называют последовательностью частных (частичных) сумм ряда (1).
Определение 2. Если последовательность частичных сумм ряда (1) является сходящейся, то ряд (1) называют сходящимся, а число 
называют суммой ряда.
В случае выполнения определения 2 используют запись
.
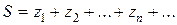
Если последовательность расходится, то ряд (1) называют расходящимся.
Примеры. 1)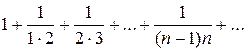 
.
Заметим, что 
, 
. Тогда
, 
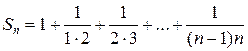
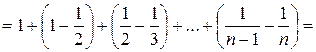
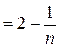. Ряд сходится, его сумма равна 2.
.
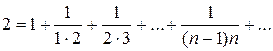2) .
, 
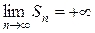. Ряд расходится.
3) 
.
; 
; 
; 
; ... . 
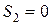. Предела не существует, ряд расходится.
Замечание. Итак, видим, что если дан ряд
(1)
то ему в соответствие ставится последовательность , где 
, сходимость которой изучается.
Обратно, если дана последовательность , то можно построить ряд, частными суммами которого будут члены последовательности . Это ряд вида
.
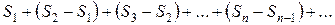Таким образом, становится понятным, что теория рядов есть иная форма теории последовательностей.
Из определения сходимости ряда вытекает простая
Теорема. Если ряд (1) сходится, то при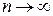 
общий член ряда стремится к нулю.
Доказательство. В прежних обозначениях имеем:
,
что и требовалось доказать.
Замечание 1. Теорема выражает необходимый признак сходимости ряда. Из него вытекает, что если общий член ряда при 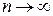не стремится к нулю, то ряд расходится.
Примеры.1) , 
, ряд расходится.
2) , 
0 при 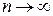, ряд расходится.
Замечание 2. Необходимый признак сходящегося ряда не является достаточным, то есть ряд с общим членом, стремящимся к нулю, может расходиться.
Пример. Рассмотрим ряд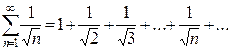 
. Заметим, что 
при 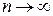. Далее 
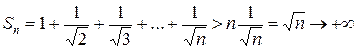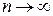при . Ряд расходится.
В заключении рассмотрим важный в теории рядов пример ряда.
Рассмотрим геометрическую прогрессию
,
где 
, q – комплексные числа. Образуем ряд
.
Этот ряд, обычно, также называют геометрической прогрессией.
Выясним, когда этот ряд сходится. Ясно, что если 
, то ряд расходится. Действительно, рассмотрим общий член ряда 
. Имеем 
, 
0 при 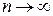. Следовательно, 0 при 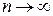, и в силу необходимого признака ряд расходится.
Пусть теперь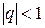 
. В этом случае ясно, что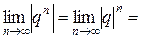 
. Далее
,
.
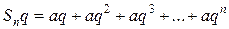Вычтем из первой суммы вторую. Получим 
, откуда
.
Тогда 
.
Итак, при |q| ≥ 1 ряд расходится, а при |q| < 1
.