 |
|
Признаки сравнения положительных рядов
Если дан какой-либо ряд, то является важным установление факта сходимости или расходимости данного ряда. Применение для этого критерия Коши, как правило, является затруднительным. Поэтому желательным является выяснение удобных на практике признаков сходимости рядов. Рассмотрение таких признаков мы начнем для рядов с действительными и неотрицательными числами.
Ряд
(1)
будем называть положительным, если 
, 
1, 2, ... .
Начнём с вспомогательного простого предложения.
Теорема 1. Для того чтобы положительный ряд (1) сходился, необходимо и достаточно, чтобы последовательность 
его частных сумм была ограничена сверху.
Доказательство. 1) Необходимость. Сходимость ряда есть сходимость последовательности его частичных сумм. Но сходящаяся последовательность ограничена.
2) Достаточность. Для положительного ряда последовательность его частных сумм, очевидно, является неубывающей
.
Если же последовательность ограничена сверху, то по известной теореме она имеет предел.
Теперь рассмотрим признаки сравнения рядов.
Теорема 2. Пусть даны положительные ряды 
(1) и 
(2), и 
для всех n. Тогда из сходимости ряда (2) следует сходимость ряда (1), и, следовательно, из расходимости ряда (1) следует расходимость ряда (2).
Доказательство. Пусть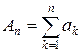 
, 
. Так как для всех n, то и
(3)
для всех n.
Пусть 
. Из неравенств (3) и неубывания 
вытекает, что
для всех n. Тогда из теоремы 1 следует сходимость ряда (1).
Примеры. 1) Исследовать на сходимость ряд
.
Рассмотрим ряд
,
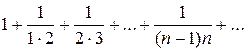который, как показано в §1, сходится. Очевидно, что
, 2, 3, ... .
Тогда по доказанной теореме исходный ряд сходится.
2) Исследовать на сходимость ряд
.
Сравним этот ряд с рядом
,
который расходится. Так как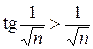 
, то данный ряд расходится.
Из доказанной теоремы вытекает предельный признак сравнения рядов, удобный на практике.
Предварительно введем простое понятие. Ряд будем называть строго положительным, если 
для всех n.
Теорема 3. Пусть даны строго положительные ряды (4) и (5) и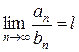 
, 
. Тогда ряды (4) и (5) сходятся или расходятся одновременно.
Доказательство. Пусть число ε такое, что 
. В силу определения предела
.
Тогда
(6)
при 
.
Если сходится ряд , то в силу теоремы об умножении ряда на число сходится и ряд 
. Но тогда по теореме об эквивалентности сходимости ряда и его остатка сходится ряд 
. Из неравенств (6) и теоремы 2 следует сходимость ряда 
, следовательно, и ряда .
Аналогично, если сходится ряд , то из неравенств (6) и теоремы 2 сходится ряд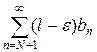 
. Умножив последний ряд на 
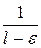, получаем сходящийся ряд 
. Тогда сходится ряд .
Примеры. 1) Исследовать на сходимость ряд
.
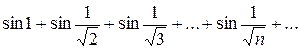Сравним ряд с расходящимся рядом 
. Так как 
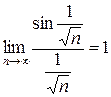, то данный ряд расходится.
Заметим, что в этом примере непосредственно теорему 2 применить нельзя, так как 
.
2) Исследовать на сходимость ряд 
.
Сравним ряд с рядом 
, который сходится. Так как 
,
то данный ряд сходится.
Замечание.Если в условиях теоремы 
, то можно утверждать, что из сходимости ряда (5) следует сходимость ряда (4). Действительно, если 
при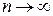 
, то, начиная с некоторого номера, 
или, следовательно, 
. Далее работает теорема 2.
Если же в теореме 
, то из расходимости ряда (4) следует расходимость ряда (5). Действительно, если 
при 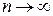, то с некоторого номера 
или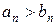 
. Далее вновь применяем теорему 2.