 |
|
Абсолютно и условно сходящиеся ряды
Определение 1. Пусть дан произвольный ряд с комплексными числами
 . (1)
. (1)
Образуем ряд из модулей членов ряда (1)
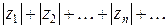 . (2)
. (2)
Это положительный ряд. Если ряд (2) сходится, то ряд (1) называется абсолютно сходящимся. Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.
Ясно, что всякий положительный сходящийся ряд является абсолютно сходящимся.
Примеры.1)  (3)
(3)
Это абсолютно сходящийся ряд, так как сходится ряд
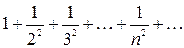 .
.
2) 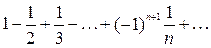 . (4)
. (4)
Этот ряд по признаку Лейбница сходится. Образуем ряд из абсолютных величин данного ряда
 .
.
Этот ряд расходящийся. Таким образом, исходный ряд сходится условно.
3)  .
.
Легко видеть, что ряд из реальных частей данного ряда есть ряд (3), а ряд из мнимых частей ряда есть ряд (4). Вспоминая положение о соотношении между сходимостью ряда с комплексными числами и сходимостью рядов из реальных и мнимых частей, видим, что данный ряд сходится.
Образуем ряд из модулей данного ряда
 . (5)
. (5)
Видим, что  , а ряд
, а ряд  расходится. Тогда по признаку сравнения расходится ряд (5). Таким образом, исходный ряд сходится условно.
расходится. Тогда по признаку сравнения расходится ряд (5). Таким образом, исходный ряд сходится условно.
Будет ли абсолютно сходящийся ряд сходящимся?
Теорема 1.Абсолютно сходящийся ряд является сходящимся.
Доказательство. Пусть дан ряд (1). В силу условия теоремы сходится ряд (2). Тогда для него выполняется критерий Коши сходимости
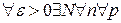
 . (6)
. (6)
Учитывая, что

при любых n и p, из (6) получаем

 .
.
Это означает, что для ряда (1) выполнен критерий Коши, и, значит, ряд сходится.
Для исследования рядов на абсолютную сходимость применяются признаки сходимости положительных рядов, так как в этом случае приходится рассматривать положительный ряд (2).
Сформулируем их применительно к нашему случаю.
Теорема 2.Пусть дан ряд (1) и положительный сходящийся ряд
 (7)
(7)
Если для всех n  , то ряд (1) сходится абсолютно.
, то ряд (1) сходится абсолютно.
Доказательство. Дело сводится к признаку сравнения положитель-ных рядов применительно к рядам (2) и (7).
Аналогично можно перефразировать предельный признак сравнения рядов.
Теорема 3. (Даламбер)Если для ряда (1) существует конечный или бесконечный предел
 ,
,
то при  ряд сходится абсолютно, а при
ряд сходится абсолютно, а при  ряд расходится.
ряд расходится.
Доказательство. 1) Если  , то по признаку Даламбера ряд (2) сходится, что означает абсолютную сходимость ряда (1).
, то по признаку Даламбера ряд (2) сходится, что означает абсолютную сходимость ряда (1).
2) Если  , то, как это следует из доказательства признака Даламбера, общий член ряда (2) не стремится к нулю. Но тогда не выполняется необходимый признак сходимости и для ряда (1). Ряд (1) расходится.
, то, как это следует из доказательства признака Даламбера, общий член ряда (2) не стремится к нулю. Но тогда не выполняется необходимый признак сходимости и для ряда (1). Ряд (1) расходится.
Замечание. Можно перефразировать признак Даламбера и в непредельной форме.
Теорема 4. (Коши-Адамар)Пусть дан ряд (1) и
 .
.
При  ряд сходится абсолютно, при
ряд сходится абсолютно, при  ряд расходится.
ряд расходится.
Доказательство теоремыдословно такое же, как и теоремы 3.
Если предполагать для ряда (1) существование предела  , то теорема 4 превращается в признак Коши.
, то теорема 4 превращается в признак Коши.
Примеры.1)  .
.
Рассмотрим положительный сходящийся ряд
 .
.
Так как для всех 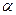
 , то данный ряд сходится абсолютно для любого
, то данный ряд сходится абсолютно для любого 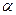 .
.
2)  .
.
Так как  , то ряд сходится абсолютно.
, то ряд сходится абсолютно.